目前计划:
课程方面 周一、三、五学习MIT的线性代数 链接,周二、四、六学习Berkeley的算法课 链接
书本方面 周一、三、五学习图像处理,周二、四、六学习西瓜书,周三、周六学习统计学习方法 GitHub链接
周日完成西瓜书后面的习题,适当完成统计学习方法的代码,查漏补缺并整理报告
每天至少三小时,尽量达到四小时以上,少的时间要尽快补上
代码部分,继续之前的tensorflow2.0深度学习一书,完成了第十一章和第十二章,分别是循环神经网络和自编码器。学习了各种循环神经网络以及各种自编码器的原理,完成了LSTM/GRU在IMDB数据集上的语义分析,Auto-encoder以及VAE。其中关于VAE的数学推导比较复杂,我手推了一遍,代码上传到了github上,在根目录的tensorflow2.0_study文件夹下,VAE的推导上传到了根目录的Noncoding_homework下。
书本部分,阅读《统计学习方法》2-4章,笔记上传到了github上,在根目录的Statistic_Note文件夹下。
本周主要学习了半监督学习的GNN,GCN,以及无监督学习的Auto-encoders和VAE。
先从相对较简单的Auto-encoder开始。
在编写autoencoder的程序中,发现书中在比较两张图片用的tf.nn.sigmoid_cross_entropy_with_logits作为损失函数。这个函数的作用是计算经sigmoid 函数激活之后的交叉熵。它适用于分类的类别之间不是相互排斥的场景,即多个标签(如图片中包含狗和猫)。
与之相对应的是tf.nn.softmax_cross_entropy_with_logits,它对于输入的logits先通过softmax函数计算,再计算它们的交叉熵,但是它对交叉熵的计算方式进行了优化,使得结果不至于溢出。
它适用于每个类别相互独立且排斥的情况,一幅图只能属于一类,而不能同时包含一条狗和一只大象。
自编码器训练较稳定,但是由于损失函数是直接度量重建样本与真实样本的底层特征之间的距离,而不是评价重建样本的逼真度, 因此在某些任务上效果一般,如图片重建,容易出现重建图片边缘模糊,逼真度相对真实图片仍有不小差距。
了防止神经网络记忆住输入数据的底层特征, Denoising Auto-Encoders 给输入数据添加噪声后,网络需要从𝒙 ̃学习到数据的真实隐藏变量 z,并还原出原始的输入𝒙 添加随机的噪声扰动,如给输入𝒙添加采样自高斯分布的噪声𝜀
自编码器网络同样面临过拟合的风险, Dropout Auto-Encoder 通过随机断开网络的连接来减少网络的表达能力,防止过拟合。
对于普通的函数f(x),我们可以认为f是一个关于x的一个实数算子,其作用是将实数x映射到实数f(x)。那么类比这种模式,假设存在函数算子F,它是关于f(x)的函数算子,可以将f(x)映射成实数F(f(x)) 。对于f(x)我们是通过改变x来求出f(x)的极值,而在变分中这个x会被替换成一个函数y(x),我们通过改变x来改变y(x),最后使得F(y(x))求得极值。
变分:指的是泛函的变分。打个比方,从A点到B点有无数条路径,每一条路径都是一个函数吧,这无数条路径,每一条函数(路径)的长度都是一个数,那你从这无数个路径当中选一个路径最短或者最长的,这就是求泛函的极值问题。有一种老的叫法,函数空间的自变量我们称为宗量(自变函数),当宗量变化了一点点而导致了泛函值变化了多少,这其实就是变分。变分,就是微分在函数空间的拓展,其精神内涵是一致的。求解泛函变分的方法主要有古典变分法、动态规划和最优控制。
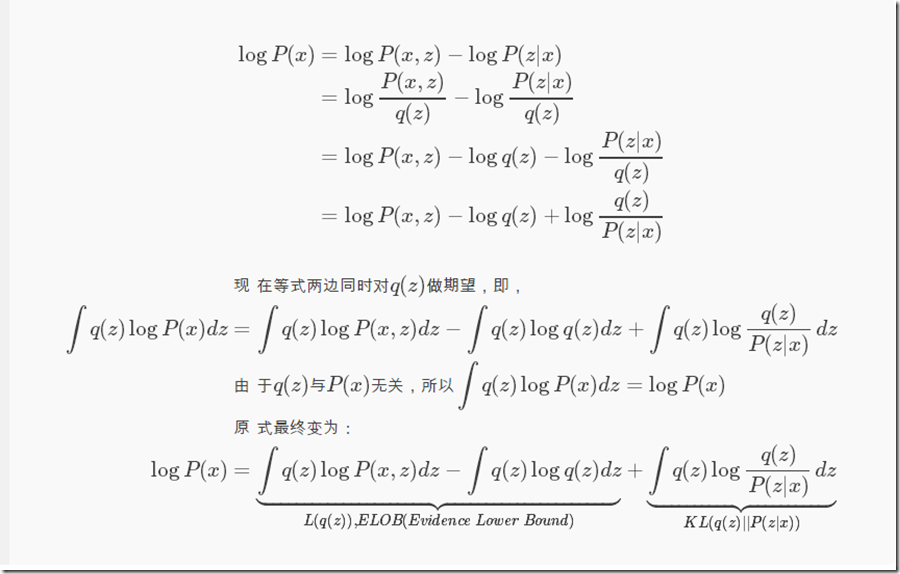
对于一类数据x(无论是音频还是图片),对它们进行编码后得到的特征数据往往服从某种分布q(z),z为隐变量,q(z)这个隐含分布我们无法得知,但是我们可以通过现有数据X来推断出q(z),即P(z|x)。KL散度是用来衡量两个分布之间的距离,当距离为0时,表示这两个分布完全一致。P(x)不变,那么想让KL(q(z)||P(z|x))越小,即让ELOB越大,反之亦然。因为KL≥0,所以logP(x)≥ELOB。
隐变量 采样自编码器的输出𝑞 ( z| x),如图 12.11 左所示,编码器输出正态分布的值𝜇和方差𝜎2,解码器的输入采样自𝒩(𝜇, 𝜎2)。由于采样操作的存在,导致梯度传播是不连续的,无法通过梯度下降算法端到端式训练 VAE 网络。
它通过 = 𝜇 + 𝜎 ⊙ 𝜀方式采样隐变量 z, 𝜀变量采样自标准正态分布𝒩(0, 𝐼), 𝜇和𝜎由编码器网络产 生,通过 = 𝜇 + 𝜎 ⊙ 𝜀即可获得采样后的隐变量 。
最早的图神经网络起源于Franco博士的论文, 它的理论基础是不动点理论。给定一张图 G,每个结点都有其自己的特征(feature),连接两个结点的边也有自己的特征。GNN的学习目标是获得每个结点的图感知的隐藏状态
我们还需要另外一个函数 g 来描述如何适应下游任务。 $$ 𝐨_𝑣=𝑔(𝐡_𝑣,𝐱_𝑣) $$ 在原论文中,g 又被称为局部输出函数(local output function),与 ff类似,gg也可以由一个神经网络来表达,它也是一个全局共享的函数。
GNN的理论基础是不动点(the fixed point)理论,这里的不动点理论专指巴拿赫不动点定理(Banach's Fixed Point Theorem)。首先我们用 F表示若干个f堆叠得到的一个函数,也称为全局更新函数,那么图上所有结点的状态更新公式可以写成:$𝐇^{𝑡+1}=F(𝐇^𝑡,𝐗)$
不动点定理指的就是,不论$H^0$是什么,只要 $F $ 是个压缩映射(contraction map),$H^0$经过不断迭代都会收敛到某一个固定的点,我们称之为不动点。
为了实现f是压缩映射,我们需要雅可比矩阵(Jacobian Matrix)的惩罚项(Penalty)来实现。在代数中,有一个定理是: f 为压缩映射的等价条件是 f 的梯度/导数要小于1。根据拉格朗日乘子法,将有约束问题变成带罚项的无约束优化问题,训练的目标可表示成如下形式: $$ J = Loss + \lambda \cdot \max({\frac{||{\partial}FNN||}{||{\partial}\mathbf{h}||}}−c,0), c\in(0,1) $$ 其中$λ$是超参数,与其相乘的项即为雅可比矩阵的罚项。
初代GNN,也就是基于循环结构的图神经网络的核心是不动点理论。它的核心观点是通过结点信息的传播使整张图达到收敛,在其基础上再进行预测。收敛作为GNN的内核,同样局限了其更广泛的使用,其中最突出的是两个问题:
- GNN只将边作为一种传播手段,但并未区分不同边的功能。
- 如果把GNN应用在图表示的场景中,使用不动点理论并不合适。这主要是因为基于不动点的收敛会导致结点之间的隐藏状态间存在较多信息共享,从而导致结点的状态太过光滑,并且属于结点自身的特征信息匮乏。
GCN精妙地设计了一种从图数据中提取特征的方法,从而让我们可以使用这些特征去对图数据进行节点分类(node classification)、图分类(graph classification)、边预测(link prediction) ,还可以顺便得到 图的嵌入表示(graph embedding)
与CNN相比,在一个图中,邻居的数量、顺序是无法确定的,因此无法找到一个和CNN一样的卷积核。但我们仍然希望借助CNN的思想。它利用图的**拉普拉斯矩阵(Laplacian matrix)**导出其频域上的的拉普拉斯算子,再类比频域上的欧式空间中的卷积,导出图卷积的公式。
如何定义非欧几里得结构上的卷积?
定义:
邻接矩阵A
度矩阵D:对角矩阵,表示每一个节点的度
拉普拉斯矩阵L:L=D-A,下面公式中的L是经过标准化的
GCN的核心基于拉普拉斯矩阵的谱分解。
拉普拉斯算子Δ 的物理意义是空间二阶导: $$ ∆{\exp}^{-2{\pi}ixt}=\frac{{\partial}^2}{{\partial}t^2}{\exp}^{-2{\pi}ixt}={-4{\pi}^2x^2}{\exp}^{-2{\pi}ixt} $$
而对应到图中,L就是拉普拉斯算子,其特征向量u即为 $ {\exp}^{-2{\pi}ixt}$
图卷积算子: $$ h^{l+1}{:,j}={\sigma}(U{\sum}{i=1}^{d_l}{\Theta}^l_{i,j}U^Th^l_{:,i}) $$
$$ {\Theta}^l_{i,j}=g_{\theta}= \left[ \begin{matrix} {\theta}1 & ... & 0 \ ... & ... & ... \ 0 & ... & {\theta}N \end{matrix} \right] $$ gθ就是GCN的卷积核,为$U^Tg$,需要计算拉普拉斯矩阵的特征值和特征向量,计算量巨大,在论文 Convolutional neural networks on graphs with fast localized spectral filtering中,应用**切比雪夫多项式(Chebyshev polynomials)**来加速特征矩阵的求解。假设切比雪夫多项式的第k项是 $T{k}$, 频域卷积核的计算方式如下: $$ g{\theta}={\sum}{k=0}^{K-1}{\theta}{k}T_{k}(\tilde{\Lambda}), \text{where}\ \tilde{\Lambda}=\displaystyle\frac{2\Lambda}{\lambda_{max}}-I_N $$
这篇论文通过主要通过GCN的算法进行不规则图片(brain networks)相似度的衡量。已将学习笔记上传到github中,在根目录的PaperNote文件夹下。
由于我读过的论文比较少,对许多的背景知识了解的比较浅,比如说Brain Connectivity Graph, fMRI, Brain ROI等等知识点,只能对抽象出来的方法进行一个理解。
这篇论文首先讲了一些传统的相似度学习的方法,比如graph embedding, motif counting等等。我在网上学习了一下graph embedding的算法。**Embedding在数学上是一个函数,将一个空间的点映射到另一个空间,通常是从高维抽象的空间映射到低维的具象空间。Embeding的意义将高维数据转换到低维利于算法的处理;同时解决one-hot向量长度随样本的变化而变化,以及无法表示两个实体之间的相关性这一问题。其中DeepWalk是一种解决方案,通过在图上随机游走得到节点序列,然后套一个word2vector这样的算法就能得到表示。DeepWalk的进阶则是node2vector,在DeepWalk的基础上更进一步,通过调整随机游走权重的方法使graph embedding的结果在网络的同质性(homophily)和结构性(structural equivalence)**中进行权衡权衡。而同质性用的是BFS,结构性用的是DFS。
接着这个论文展示了自己的网络模型。首先是将原始的fMRI timeseries转化乘labelled graph。用的是k-NN得到平均functional-connectivity matrix。之所以要平均是因为每个图的拉普拉斯矩阵的特征值是不一样的,因此卷积核是独占的。其实在这里我是有许多不理解的,主要是由于我对背景的不清晰,这个我在之后会补上。在得到图之后经过两个GCN网络,并将两个结果点乘再经过fc得到最终判断similarity的vector。
接着就是对GCN的介绍。我在前面已经写过,这儿不再赘述。
接着讨论了三种loss函数,分别是hinge loss, global loss,和作者自己改进后的constrained variance loss。hinge loss最为直接,”最大化边缘“分类,并没有对网络输出的variance进行约束;global loss分为两部分,最大化均值的差距,同时最小化标准差,而constrained variance在global loss的基础上增加了一个a作为标准差的门限,只要不大于这个门限都不会被惩罚。
后面的结果部分和讨论部分还没有看,本周看完。
主要进行代码方面的练习,顺便巩固了基础知识。
将tensorflow2.0深度学习一书从第一章学习到第十章结束,手写了其中大部分的代码。包括手写神经网络的求导、正向传播、反向传播等过程,线性回归、逻辑回归问题,MPG预测,以及tensorflow2.0和keras的新的特性。与图像结合比较紧密的是LeNet5,VGG13, ResNet18的手写实现,且以在本地跑通,代码上传到了github上,在根目录的tensorflow2.0_study文件夹下。
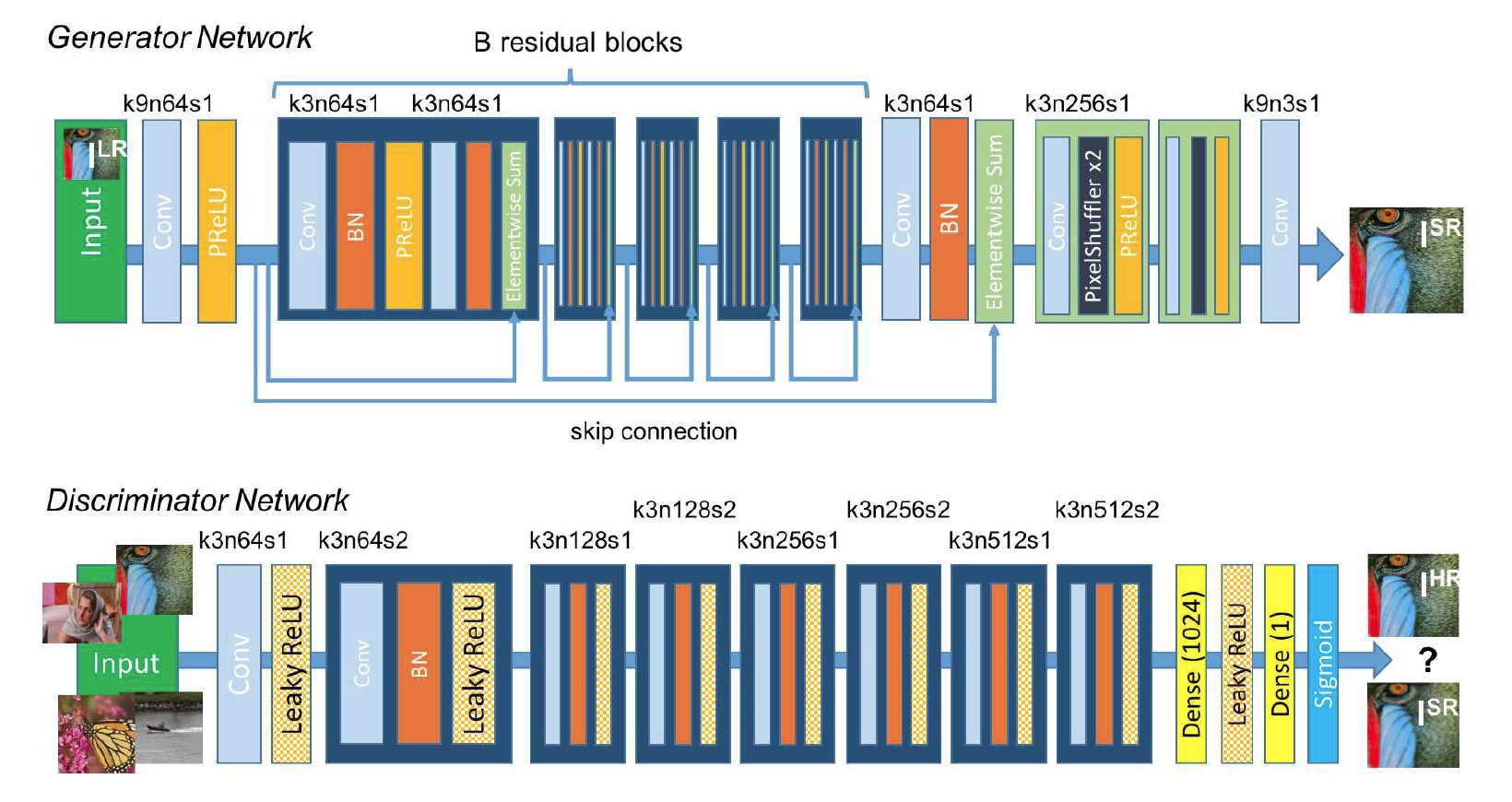
在论文方面了解了一些超分辨率有关的东西,大致知道了一些超分辨率的算法,这些算法也是我之后学习的方向。并着重看了SRGAN的文章(Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network),这篇文章将我前一段时间学习的GAN,ResNet,VGG结合在了一起,我对这篇文章做了一些笔记做了一些笔记,同时上传到github中,在根目录的PaperNote文件夹下。
这篇论文的核心是批评传统的MSE作为loss的一些监督学习的方法,用MSE作loss的方法容易使图片变得过于顺滑,失去了边缘的一些信息以及高频的信息。此外,作者改进了两点,一是loss函数的改进,改成了content loss和adversial loss的和,其中content loss也不再使用MSE而是使用训练好的VGG网络得到特征进行pixel-wise的对比得到loss,二是对GAN本身的改进,将深度ResNet融入到generator的训练之中,此外还有一些小的细节,如BN层,训练filters等等,以期获得更好的结果。
在学习过程中记录了一些知识或是一些关键的内容:
转置卷积具有“放大特征图”的功能,在生成对抗网络、语义分割等中得到了广泛应 用,如 DCGAN (Radford, Metz, & Chintala, 2015)中的生成器通过堆叠转置卷积层实现逐层 “放大”特征图,最后获得十分逼真的生成图片。
从上图中可以看到,生成器G 将一个100 维的噪音向量扩展成64 * 64 * 3 的矩阵输出,整个过程采用的是微步卷积的方式。作者在文中将其称为fractionally-strided convolutions,并特意强调不是deconvolutions。
上采样和去卷积是同一个概念,它的目的是将经过池化层以后缩小的矩阵扩大到一定的大小,比如说从3 * 3 扩大到5 * 5,如下图所示:
而去卷积(链接:反卷积)又包含转置卷积和微步卷积,两者的区别在于padding 的方式不同,看看下面这张图片就可以明白了:
代码如下:
In [14]:
# 创建 4x4 大小的输入
x = tf.range(16)+1
x = tf.reshape(x,[1,4,4,1])
x = tf.cast(x, tf.float32)
# 创建 3x3 卷积核
w = tf.constant([[-1,2,-3.],[4,-5,6],[-7,8,-9]])
w = tf.expand_dims(w,axis=2)
w = tf.expand_dims(w,axis=3)
# 普通卷积运算
out = tf.nn.conv2d(x,w,strides=1,padding='VALID')
Out[14]:
<tf.Tensor: id=42, shape=(2, 2), dtype=float32, numpy=
array([[-56., -61.],
[-76., -81.]], dtype=float32)>
In [15]: # 恢复 4x4 大小的输入
xx = tf.nn.conv2d_transpose(out, w, strides=1, padding='VALID',
output_shape=[1,4,4,1])
tf.squeeze(xx)
tf.squeeze(xx)
Out[15]:
<tf.Tensor: id=44, shape=(4, 4), dtype=float32, numpy=
array([[ 56., -51., 46., 183.],
[-148., -35., 35., -123.],
[ 88., 35., -35., 63.],
[ 532., -41., 36., 729.]], dtype=float32)>BN的基本思想其实相当直观:因为深层神经网络在做非线性变换前的激活输入值(就是那个x=WU+B,U是输入)随着网络深度加深或者在训练过程中,其分布逐渐发生偏移或者变动,之所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近(对于Sigmoid函数来说,意味着激活输入值WU+B是大的负值或正值),所以这导致后向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因,而BN就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正太分布而不是萝莉分布(哦,是正态分布),其实就是把越来越偏的分布强制拉回比较标准的分布,这样使得激活输入值落在非线性函数对输入比较敏感的区域,这样输入的小变化就会导致损失函数较大的变化,意思是这样让梯度变大,避免梯度消失问题产生,而且梯度变大意味着学习收敛速度快,能大大加快训练速度。
Skip Connection 的思想在 ResNet 上面获得了巨大的成功,研究人员开始尝试不同的Skip Connection 方案,其中比较流行的就是 DenseNet (Huang, Liu, & Weinberger, 2016)。DenseNet 将前面所有层的特征图信息通过 Skip Connection 与当前层输出进行聚合,与ResNet 的对应位置相加不同, DenseNet 采用在通道轴 c 维度进行拼接操作, 聚合特征信息 。
输入𝑥0通过H1卷积层得到输出𝑥1, 𝑥1与𝑥0在通道轴上进行拼接,得到聚合后的特征张量,送入H2卷积层,得到输出𝑥2,同样的方法, 𝑥2与前面所有层的特征信息: 𝑥1与𝑥0进行聚合,再送入下一层。如此循环,直至最后一层的输出𝑥4和前面所有层的特征信息: {𝑥𝑖}𝑖=0 1 2 3进行聚合得到模块的最终输出。这样一种基于 Skip Connection 稠密连接的模块叫做 Dense Block。
SRGAN的网络结构如图所示:
该研究中的损失函数可分为两个部分:对抗损失(adversarial loss )和内容损失(content loss)。在较高层面上,对抗损失使图像看起来更自然;内容损失则保证重建图像与低分辨率原始图像有相似的特点。其中,对抗损失和传统的 GANs 应用类似,创新的是内容损失。该研究中的内容损失,可被看作为重建的高分辨率图像和原始高分图像之间特征图(feature map)的欧式距离(Euclidean distance)损失。而 GAN 的损失函数是对抗损失和内容损失的加权和。
其中content loss有两种可选,一种是传统的MSE,一种是VGG19的loss。
而adversarial loss是: $$ l_{Gen}^{SR}=\sum ^{N}{n=1}-\log D{\theta {d}}\times \left( G{\theta _{G}}\left( I^{u^{2}}\right) \right) $$ 这个式子代表了重构的图片是真实的高分辨率图片的概率。
为了更好的梯度表现,我们最小化上面的式子而不是最小化log(1-D(G(I)))
1.使用MSEloss预训练一个生成器
2.正式开始训练SRGAN,将各级loss清零,初始化label,并分别为真假label赋值
3.第一遍G生成图和真图一起输入D,然后在D中进行判别,训练D
4.再次训练G,循环往复
通过李宏毅的教程详细学习了GAN的数学理论以及各种应用与变种,并且结合实际案例(生成各种种类的图片)编写代码更新到Coding_homework/下,整理了学习笔记到GAN/下,整理了一份报告到GAN/下。
强化了动态规划算法的学习,继续往后推进了四节课,已更新笔记。
继续往后推进了5课,已更新笔记。
决策树结束。
3.5各向异性扩散涉及到热方程的并没有理解,先mark一下
了解了各种算子的特征(优点以及缺点),平均算了可以去除大量噪声,但是使特征边界模糊;高斯平均保留更多特征,但与直接求平均相比,几乎没有优势(噪声不是高斯分布的);中值算子保留些噪声,但得到清晰的边界特征;截断中值算子去除更多噪声,但也去除更多图像细节。很显然,由图3.24(b)和图3.24(c)的结果表明,加大截断中值模板可以提高性能。这是预料之中的,由于通过加大截断中值模板,实质上可以加大分布,从中找出模式。
第四章讲的是低层次特征提取以及边缘检测。最基本的是差分+均匀阈值方法。并且学习了分块阈值方法, 以便每个块的光照都近似均匀的 。学习链接.
接着从数学角度(泰勒展开)理解了边缘检测算子。并学习了更多的边缘检测算子,如Prewitt, Sobel(帕斯卡三角形), 并从频域角度理解了Sobel算子,复习了z变换。接着学习了Canny算子和滞后阈值。
二阶算子:包括拉普拉斯算子,Marr-Hildreth(高斯算子与图像进行卷积后进行二阶微分,同时包含微分和平滑,这个算子与人类视觉密切关系,具有多分辨率分析能力)。
比较了各种 边缘检测算子: 中值滤波常用于一般性(非超声波)的程序处理,作为预滤波器用于一阶和二阶方法效果显著;所有边缘算子的结果都是用滞后阈值处理来实现的,其中,为了更好地反映其性能,这些阈值都是手动选择的。Prewitt 和Sobel 算子显示了一些边界,但处理后的图像中仍然保留了许多噪声(Sobel少一点);Laplacian 算子对于大噪声的图片几乎没有留下什么信息;Mar- Hildreth方法的处理结果有了一些改善,对于如此大噪声的图像,很难选择个大小适当的LoG算子来检测如此多维的特征,在噪声过滤所需的算子大小与目标特征的大小之间需要折中;Canny 和Spacek算子的处理效果非常好。
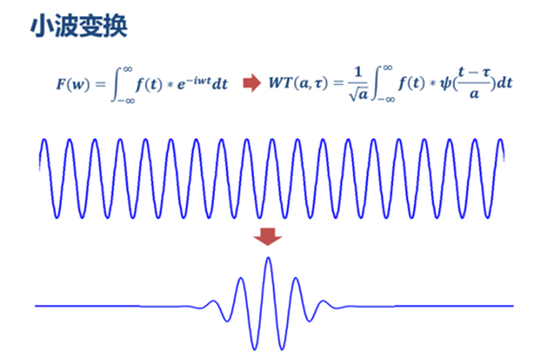
为了进一步学习相位一致性,学习了小波变换,了解了傅立叶变换的弱点以及小波变换的优势。学习链接.
做傅里叶变换只能得到一个频谱,做小波变换却可以得到一个时频谱!
为了学习通过亮度变化计算曲率,学习了图像梯度。学习链接
第一章从宏观上把握了机器学习到底是什么,可以用来干什么,发展历史,目前发展到了什么地步,大概是怎么样的一个操作流程。学习了一些机器学习方面的专有名词。根据训练数据是否有标记信息,学习任务大致可以划分为两大类:监督学习和无监督学习,分类和回归是前者的代表,聚类是后者的代表。了解了泛化性、假设空间、归纳偏好等等概念。
第二章开始我觉觉得稍微有点硬核了,数学表达式多了起来,用到了很多以前微积分、概率论、线性代数中的知识,我也因此决定要认认真真补一补数学的基础,包括MIT的线性代数以及统计学习方法。这一章学习了如何评估自己的学习器。我们希望得到泛化误差小的学习器。然而我们无法直接比较泛化误差,因此有了这一章的许许多多的评估方法。最基本的是留出法,即按一定比例留出一部分样本当测试集,用测试集来评估误差,作为对泛化误差的估计。接着学习了更加高级有效的交叉验证以及交叉验证的特例,留一法,并编写代码验证了这两种验证的方法。当数据量不太够的时候,我们也可以使用自助法。为了调参,还可以在训练数据中分一部分作为验证集:
性能度量最常用的是均方误差,错误率,以及精度。接着就是使我晕头转向的TP, TN, FP, FN, TPR, FPR, TNR, FNR这一系列概念以及它们之间的关系,它们可以组合出F1度量,P-R曲线,ROC曲线(纵轴为真正利率TPR,纵轴为假正例率FPR),如何绘制ROC曲线,AUC(ROC曲线下面的面积),以及如何通过P-R曲线、ROC曲线判断学习器的性能。接着推广到更一般的代价敏感错误率与代价曲线,考虑到FP和FN的代价在现实中并不一样。
之后是基于统计学的比较检验。由于学概率论已经是一年多以前了,因此对 χ2分布 ,t分布,F分布已经有点模糊了,经过好长一段时间资料的搜索以及回忆过后,大概搞明白对于单个学习器来说,可以假设它的泛化性能并通过t分布检验。如果是要对两个不同学习器的性能进行比较,可以使用交叉验证t检验McNemar检验( χ2分布 检验)以及较为复杂(其实是还没搞明白)的Friedman检验。
最后了解了机器学习中泛化误差、偏差与方差的关系:
第三章讲的是线性模型,学习了线性回归,可以通过最小二乘法来求解,但当属性数超过样例数的时候,此时可能有很多解,常见的作法就是引入正则化项。 逻辑回归适用于分类的,引入了sigmoid函数,方便将值映射到(0,1)之间,再通过决定阈值(需要考虑类别不平衡问题进行“再缩放”),此外,对于多重分类逻辑回归模型,需要将sigmoid变成softmax。当然,多分类问题还可以拆成OvO,OvR,MvM以及ECOC编码。ECOC最佳编码是要求任意两个类别之间的编码距离越远越好(详见作业第六题)。
逻辑回归的推导运用到了概率论中所讲的极大似然法,当时有点忘了,又上网学习了一下,最大化”对数似然“,即令每个样本属于其真实标记的概率越大越好。接着又是涉及到线性代数的Hessian矩阵(然而我已经记忆模糊,只好上网再学习一番),通过Hessian矩阵判断是凸函数,可以通过梯度下降法求解。
还有一个在数学上比较硬核一些的LDA(线性判别分析),理解了它的核心思想,也通过代码实现了, 只不过推导的最后一部分还有点看不懂,可能是线性代数的知识还不够吧,先mark一下 。
第四章先看了两节,第一节让我对决策树有了一个基本的了解,并从宏观上给了实现决策树的伪代码。第二节就讲如何选择最优划分属性,我们希望分支节点所包含的样本尽量属于同一类别,即纯度尽可能高。定义了信息熵,信息熵增益,以及增益率,共同帮助决定按照什么样的顺序展开决策树。最后还对照实际的西瓜例子人工跑了一遍决策树,感觉对决策树的理解得到了巩固。