Skip to content

Latest commit

 

History

History
287 lines (233 loc) · 9.2 KB

README_EN.md

File metadata and controls

287 lines (233 loc) · 9.2 KB
comments difficulty edit_url rating source tags
true
Medium
1743
Weekly Contest 427 Q2
Binary Indexed Tree
Segment Tree
Geometry
Array
Math
Enumeration
Sorting

3380. Maximum Area Rectangle With Point Constraints I

中文文档

Description

You are given an array points where points[i] = [xi, yi] represents the coordinates of a point on an infinite plane.

Your task is to find the maximum area of a rectangle that:

  • Can be formed using four of these points as its corners.
  • Does not contain any other point inside or on its border.
  • Has its edges parallel to the axes.

Return the maximum area that you can obtain or -1 if no such rectangle is possible.

 

Example 1:

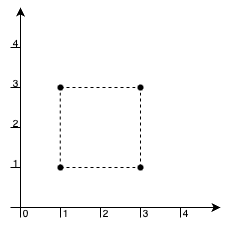
Input: points = [[1,1],[1,3],[3,1],[3,3]]

Output: 4

Explanation:

Example 1 diagram

We can make a rectangle with these 4 points as corners and there is no other point that lies inside or on the border. Hence, the maximum possible area would be 4.

Example 2:

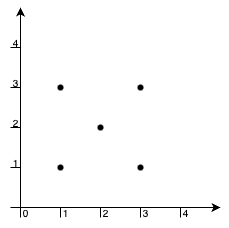
Input: points = [[1,1],[1,3],[3,1],[3,3],[2,2]]

Output: -1

Explanation:

Example 2 diagram

There is only one rectangle possible is with points [1,1], [1,3], [3,1] and [3,3] but [2,2] will always lie inside it. Hence, returning -1.

Example 3:

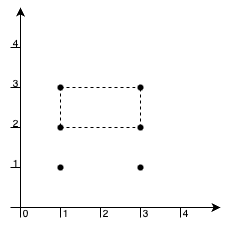
Input: points = [[1,1],[1,3],[3,1],[3,3],[1,2],[3,2]]

Output: 2

Explanation:

Example 3 diagram

The maximum area rectangle is formed by the points [1,3], [1,2], [3,2], [3,3], which has an area of 2. Additionally, the points [1,1], [1,2], [3,1], [3,2] also form a valid rectangle with the same area.

 

Constraints:

  • 1 <= points.length <= 10
  • points[i].length == 2
  • 0 <= xi, yi <= 100
  • All the given points are unique.

Solutions

Solution 1: Enumeration

We can enumerate the bottom-left corner $(x_3, y_3)$ and the top-right corner $(x_4, y_4)$ of the rectangle. Then, we enumerate all points $(x, y)$ and check if the point is inside or on the boundary of the rectangle. If it is, it does not meet the condition. Otherwise, we exclude the points outside the rectangle and check if there are 4 remaining points. If there are, these 4 points can form a rectangle. We calculate the area of the rectangle and take the maximum value.

The time complexity is $O(n^3)$, where $n$ is the length of the array $\textit{points}$. The space complexity is $O(1)$.

Python3

class Solution:
    def maxRectangleArea(self, points: List[List[int]]) -> int:
        def check(x1: int, y1: int, x2: int, y2: int) -> bool:
            cnt = 0
            for x, y in points:
                if x < x1 or x > x2 or y < y1 or y > y2:
                    continue
                if (x == x1 or x == x2) and (y == y1 or y == y2):
                    cnt += 1
                    continue
                return False
            return cnt == 4

        ans = -1
        for i, (x1, y1) in enumerate(points):
            for x2, y2 in points[:i]:
                x3, y3 = min(x1, x2), min(y1, y2)
                x4, y4 = max(x1, x2), max(y1, y2)
                if check(x3, y3, x4, y4):
                    ans = max(ans, (x4 - x3) * (y4 - y3))
        return ans

Java

class Solution {
    public int maxRectangleArea(int[][] points) {
        int ans = -1;
        for (int i = 0; i < points.length; ++i) {
            int x1 = points[i][0], y1 = points[i][1];
            for (int j = 0; j < i; ++j) {
                int x2 = points[j][0], y2 = points[j][1];
                int x3 = Math.min(x1, x2), y3 = Math.min(y1, y2);
                int x4 = Math.max(x1, x2), y4 = Math.max(y1, y2);
                if (check(points, x3, y3, x4, y4)) {
                    ans = Math.max(ans, (x4 - x3) * (y4 - y3));
                }
            }
        }
        return ans;
    }

    private boolean check(int[][] points, int x1, int y1, int x2, int y2) {
        int cnt = 0;
        for (var p : points) {
            int x = p[0];
            int y = p[1];
            if (x < x1 || x > x2 || y < y1 || y > y2) {
                continue;
            }
            if ((x == x1 || x == x2) && (y == y1 || y == y2)) {
                cnt++;
                continue;
            }
            return false;
        }
        return cnt == 4;
    }
}

C++

class Solution {
public:
    int maxRectangleArea(vector<vector<int>>& points) {
        auto check = [&](int x1, int y1, int x2, int y2) -> bool {
            int cnt = 0;
            for (const auto& point : points) {
                int x = point[0];
                int y = point[1];
                if (x < x1 || x > x2 || y < y1 || y > y2) {
                    continue;
                }
                if ((x == x1 || x == x2) && (y == y1 || y == y2)) {
                    cnt++;
                    continue;
                }
                return false;
            }
            return cnt == 4;
        };

        int ans = -1;
        for (int i = 0; i < points.size(); i++) {
            int x1 = points[i][0], y1 = points[i][1];
            for (int j = 0; j < i; j++) {
                int x2 = points[j][0], y2 = points[j][1];
                int x3 = min(x1, x2), y3 = min(y1, y2);
                int x4 = max(x1, x2), y4 = max(y1, y2);
                if (check(x3, y3, x4, y4)) {
                    ans = max(ans, (x4 - x3) * (y4 - y3));
                }
            }
        }
        return ans;
    }
};

Go

func maxRectangleArea(points [][]int) int {
	check := func(x1, y1, x2, y2 int) bool {
		cnt := 0
		for _, point := range points {
			x, y := point[0], point[1]
			if x < x1 || x > x2 || y < y1 || y > y2 {
				continue
			}
			if (x == x1 || x == x2) && (y == y1 || y == y2) {
				cnt++
				continue
			}
			return false
		}
		return cnt == 4
	}

	ans := -1
	for i := 0; i < len(points); i++ {
		x1, y1 := points[i][0], points[i][1]
		for j := 0; j < i; j++ {
			x2, y2 := points[j][0], points[j][1]
			x3, y3 := min(x1, x2), min(y1, y2)
			x4, y4 := max(x1, x2), max(y1, y2)
			if check(x3, y3, x4, y4) {
				ans = max(ans, (x4-x3)*(y4-y3))
			}
		}
	}
	return ans
}

TypeScript

function maxRectangleArea(points: number[][]): number {
    const check = (x1: number, y1: number, x2: number, y2: number): boolean => {
        let cnt = 0;
        for (const point of points) {
            const [x, y] = point;
            if (x < x1 || x > x2 || y < y1 || y > y2) {
                continue;
            }
            if ((x === x1 || x === x2) && (y === y1 || y === y2)) {
                cnt++;
                continue;
            }
            return false;
        }
        return cnt === 4;
    };

    let ans = -1;
    for (let i = 0; i < points.length; i++) {
        const [x1, y1] = points[i];
        for (let j = 0; j < i; j++) {
            const [x2, y2] = points[j];
            const [x3, y3] = [Math.min(x1, x2), Math.min(y1, y2)];
            const [x4, y4] = [Math.max(x1, x2), Math.max(y1, y2)];
            if (check(x3, y3, x4, y4)) {
                ans = Math.max(ans, (x4 - x3) * (y4 - y3));
            }
        }
    }
    return ans;
}