| comments | difficulty | edit_url | rating | source | tags | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
true |
中等 |
1743 |
第 427 场周赛 Q2 |
|
给你一个数组 points,其中 points[i] = [xi, yi] 表示无限平面上一点的坐标。
你的任务是找出满足以下条件的矩形可能的 最大 面积:
- 矩形的四个顶点必须是数组中的 四个 点。
- 矩形的内部或边界上 不能 包含任何其他点。
- 矩形的边与坐标轴 平行 。
返回可以获得的 最大面积 ,如果无法形成这样的矩形,则返回 -1。
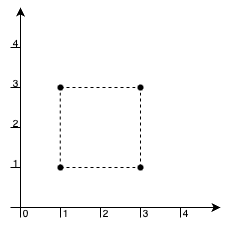
示例 1:
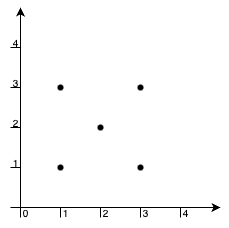
示例 2:
输入: points = [[1,1],[1,3],[3,1],[3,3],[2,2]]
输出:-1
解释:
唯一一组可能构成矩形的点为 [1,1], [1,3], [3,1] 和 [3,3],但点 [2,2] 总是位于矩形内部。因此,返回 -1 。
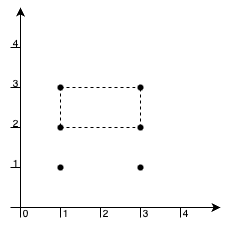
示例 3:
输入: points = [[1,1],[1,3],[3,1],[3,3],[1,2],[3,2]]
输出:2
解释:
点 [1,3], [1,2], [3,2], [3,3] 可以构成面积最大的矩形,面积为 2。此外,点 [1,1], [1,2], [3,1], [3,2] 也可以构成一个符合题目要求的矩形,面积相同。
提示:
1 <= points.length <= 10points[i].length == 20 <= xi, yi <= 100- 给定的所有点都是 唯一 的。
我们可以枚举矩形的左下角下标
时间复杂度
class Solution:
def maxRectangleArea(self, points: List[List[int]]) -> int:
def check(x1: int, y1: int, x2: int, y2: int) -> bool:
cnt = 0
for x, y in points:
if x < x1 or x > x2 or y < y1 or y > y2:
continue
if (x == x1 or x == x2) and (y == y1 or y == y2):
cnt += 1
continue
return False
return cnt == 4
ans = -1
for i, (x1, y1) in enumerate(points):
for x2, y2 in points[:i]:
x3, y3 = min(x1, x2), min(y1, y2)
x4, y4 = max(x1, x2), max(y1, y2)
if check(x3, y3, x4, y4):
ans = max(ans, (x4 - x3) * (y4 - y3))
return ansclass Solution {
public int maxRectangleArea(int[][] points) {
int ans = -1;
for (int i = 0; i < points.length; ++i) {
int x1 = points[i][0], y1 = points[i][1];
for (int j = 0; j < i; ++j) {
int x2 = points[j][0], y2 = points[j][1];
int x3 = Math.min(x1, x2), y3 = Math.min(y1, y2);
int x4 = Math.max(x1, x2), y4 = Math.max(y1, y2);
if (check(points, x3, y3, x4, y4)) {
ans = Math.max(ans, (x4 - x3) * (y4 - y3));
}
}
}
return ans;
}
private boolean check(int[][] points, int x1, int y1, int x2, int y2) {
int cnt = 0;
for (var p : points) {
int x = p[0];
int y = p[1];
if (x < x1 || x > x2 || y < y1 || y > y2) {
continue;
}
if ((x == x1 || x == x2) && (y == y1 || y == y2)) {
cnt++;
continue;
}
return false;
}
return cnt == 4;
}
}class Solution {
public:
int maxRectangleArea(vector<vector<int>>& points) {
auto check = [&](int x1, int y1, int x2, int y2) -> bool {
int cnt = 0;
for (const auto& point : points) {
int x = point[0];
int y = point[1];
if (x < x1 || x > x2 || y < y1 || y > y2) {
continue;
}
if ((x == x1 || x == x2) && (y == y1 || y == y2)) {
cnt++;
continue;
}
return false;
}
return cnt == 4;
};
int ans = -1;
for (int i = 0; i < points.size(); i++) {
int x1 = points[i][0], y1 = points[i][1];
for (int j = 0; j < i; j++) {
int x2 = points[j][0], y2 = points[j][1];
int x3 = min(x1, x2), y3 = min(y1, y2);
int x4 = max(x1, x2), y4 = max(y1, y2);
if (check(x3, y3, x4, y4)) {
ans = max(ans, (x4 - x3) * (y4 - y3));
}
}
}
return ans;
}
};func maxRectangleArea(points [][]int) int {
check := func(x1, y1, x2, y2 int) bool {
cnt := 0
for _, point := range points {
x, y := point[0], point[1]
if x < x1 || x > x2 || y < y1 || y > y2 {
continue
}
if (x == x1 || x == x2) && (y == y1 || y == y2) {
cnt++
continue
}
return false
}
return cnt == 4
}
ans := -1
for i := 0; i < len(points); i++ {
x1, y1 := points[i][0], points[i][1]
for j := 0; j < i; j++ {
x2, y2 := points[j][0], points[j][1]
x3, y3 := min(x1, x2), min(y1, y2)
x4, y4 := max(x1, x2), max(y1, y2)
if check(x3, y3, x4, y4) {
ans = max(ans, (x4-x3)*(y4-y3))
}
}
}
return ans
}function maxRectangleArea(points: number[][]): number {
const check = (x1: number, y1: number, x2: number, y2: number): boolean => {
let cnt = 0;
for (const point of points) {
const [x, y] = point;
if (x < x1 || x > x2 || y < y1 || y > y2) {
continue;
}
if ((x === x1 || x === x2) && (y === y1 || y === y2)) {
cnt++;
continue;
}
return false;
}
return cnt === 4;
};
let ans = -1;
for (let i = 0; i < points.length; i++) {
const [x1, y1] = points[i];
for (let j = 0; j < i; j++) {
const [x2, y2] = points[j];
const [x3, y3] = [Math.min(x1, x2), Math.min(y1, y2)];
const [x4, y4] = [Math.max(x1, x2), Math.max(y1, y2)];
if (check(x3, y3, x4, y4)) {
ans = Math.max(ans, (x4 - x3) * (y4 - y3));
}
}
}
return ans;
}