README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/3100-3199/3111.Minimum%20Rectangles%20to%20Cover%20Points/README_EN.md	1401	Biweekly Contest 128 Q2	Greedy Array Sorting

3111. Minimum Rectangles to Cover Points

中文文档

Description

You are given a 2D integer array points, where points[i] = [xi, yi]. You are also given an integer w. Your task is to cover all the given points with rectangles.

Each rectangle has its lower end at some point (x1, 0) and its upper end at some point (x2, y2), where x1 <= x2, y2 >= 0, and the condition x2 - x1 <= w must be satisfied for each rectangle.

A point is considered covered by a rectangle if it lies within or on the boundary of the rectangle.

Return an integer denoting the minimum number of rectangles needed so that each point is covered by at least one rectangle.

Note: A point may be covered by more than one rectangle.

 

Example 1:

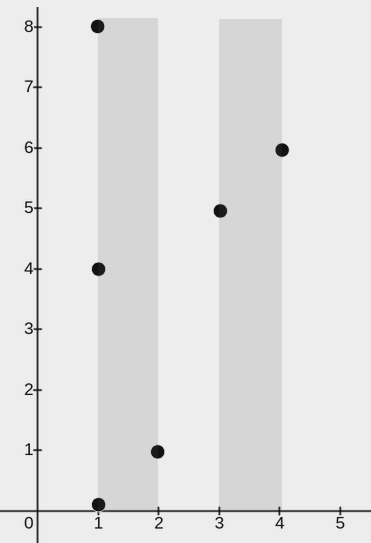
Input: points = [[2,1],[1,0],[1,4],[1,8],[3,5],[4,6]], w = 1

Output: 2

Explanation:

The image above shows one possible placement of rectangles to cover the points:

• A rectangle with a lower end at (1, 0) and its upper end at (2, 8)
• A rectangle with a lower end at (3, 0) and its upper end at (4, 8)

Example 2:

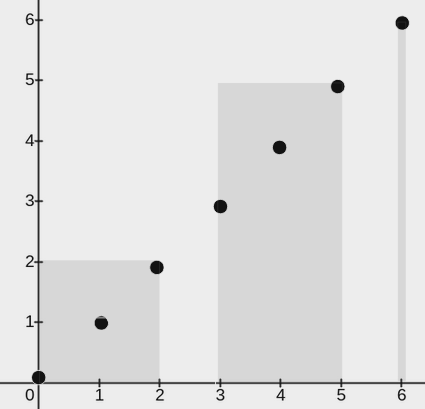
Input: points = [[0,0],[1,1],[2,2],[3,3],[4,4],[5,5],[6,6]], w = 2

Output: 3

Explanation:

The image above shows one possible placement of rectangles to cover the points:

• A rectangle with a lower end at (0, 0) and its upper end at (2, 2)
• A rectangle with a lower end at (3, 0) and its upper end at (5, 5)
• A rectangle with a lower end at (6, 0) and its upper end at (6, 6)

Example 3:

Input: points = [[2,3],[1,2]], w = 0

Output: 2

Explanation:

The image above shows one possible placement of rectangles to cover the points:

• A rectangle with a lower end at (1, 0) and its upper end at (1, 2)
• A rectangle with a lower end at (2, 0) and its upper end at (2, 3)

 

Constraints:

• 1 <= points.length <= 105
• points[i].length == 2
• 0 <= xi == points[i][0] <= 109
• 0 <= yi == points[i][1] <= 109
• 0 <= w <= 109
• All pairs (xi, yi) are distinct.

Solutions

Solution 1: Greedy + Sorting

According to the problem description, we do not need to consider the height of the rectangles, only the width.

We can sort all the points by their x-coordinates and use a variable $x_1$ to record the rightmost x-coordinate that the current rectangle can cover. Initially, $x_1 = -1$.

Next, we iterate through all the points. If the current point's x-coordinate $x$ is greater than $x_1$, it means the existing rectangle cannot cover the current point. We need to add a new rectangle, increment the answer by one, and update $x_1 = x + w$.

After completing the iteration, we obtain the minimum number of rectangles needed.

The time complexity is $O(n \times \log n)$, and the space complexity is $O(\log n)$. Here, $n$ is the number of points.

Python3

class Solution:
    def minRectanglesToCoverPoints(self, points: List[List[int]], w: int) -> int:
        points.sort()
        ans, x1 = 0, -1
        for x, _ in points:
            if x > x1:
                ans += 1
                x1 = x + w
        return ans

Java

class Solution {
    public int minRectanglesToCoverPoints(int[][] points, int w) {
        Arrays.sort(points, (a, b) -> a[0] - b[0]);
        int ans = 0, x1 = -1;
        for (int[] p : points) {
            int x = p[0];
            if (x > x1) {
                ++ans;
                x1 = x + w;
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int minRectanglesToCoverPoints(vector<vector<int>>& points, int w) {
        sort(points.begin(), points.end());
        int ans = 0, x1 = -1;
        for (const auto& p : points) {
            int x = p[0];
            if (x > x1) {
                ++ans;
                x1 = x + w;
            }
        }
        return ans;
    }
};

Go

func minRectanglesToCoverPoints(points [][]int, w int) (ans int) {
	sort.Slice(points, func(i, j int) bool { return points[i][0] < points[j][0] })
	x1 := -1
	for _, p := range points {
		if x := p[0]; x > x1 {
			ans++
			x1 = x + w
		}
	}
	return
}

TypeScript

function minRectanglesToCoverPoints(points: number[][], w: number): number {
    points.sort((a, b) => a[0] - b[0]);
    let [ans, x1] = [0, -1];
    for (const [x, _] of points) {
        if (x > x1) {
            ++ans;
            x1 = x + w;
        }
    }
    return ans;
}

Rust

impl Solution {
    pub fn min_rectangles_to_cover_points(mut points: Vec<Vec<i32>>, w: i32) -> i32 {
        points.sort_by(|a, b| a[0].cmp(&b[0]));
        let mut ans = 0;
        let mut x1 = -1;
        for p in points {
            let x = p[0];
            if x > x1 {
                ans += 1;
                x1 = x + w;
            }
        }
        ans
    }
}

C#

public class Solution {
    public int MinRectanglesToCoverPoints(int[][] points, int w) {
        Array.Sort(points, (a, b) => a[0] - b[0]);
        int ans = 0, x1 = -1;
        foreach (int[] p in points) {
            int x = p[0];
            if (x > x1) {
                ans++;
                x1 = x + w;
            }
        }
        return ans;
    }
}