| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
中等 |
1401 |
第 128 场双周赛 Q2 |
|
给你一个二维整数数组 point ,其中 points[i] = [xi, yi] 表示二维平面内的一个点。同时给你一个整数 w 。你需要用矩形 覆盖所有 点。
每个矩形的左下角在某个点 (x1, 0) 处,且右上角在某个点 (x2, y2) 处,其中 x1 <= x2 且 y2 >= 0 ,同时对于每个矩形都 必须 满足 x2 - x1 <= w 。
如果一个点在矩形内或者在边上,我们说这个点被矩形覆盖了。
请你在确保每个点都 至少 被一个矩形覆盖的前提下,最少 需要多少个矩形。
注意:一个点可以被多个矩形覆盖。
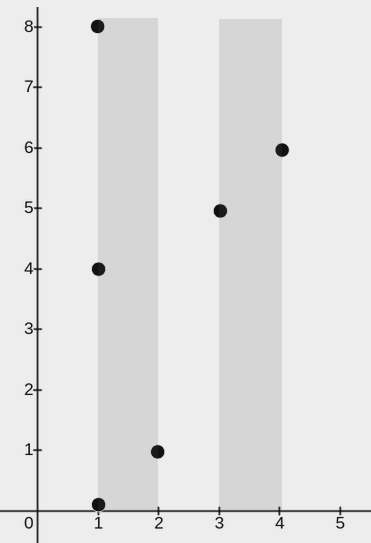
示例 1:
输入:points = [[2,1],[1,0],[1,4],[1,8],[3,5],[4,6]], w = 1
输出:2
解释:
上图展示了一种可行的矩形放置方案:
- 一个矩形的左下角在
(1, 0),右上角在(2, 8)。 - 一个矩形的左下角在
(3, 0),右上角在(4, 8)。
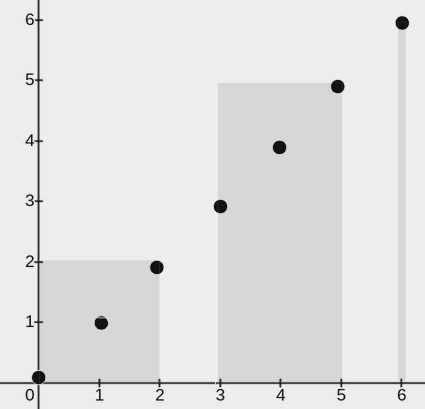
示例 2:
输入:points = [[0,0],[1,1],[2,2],[3,3],[4,4],[5,5],[6,6]], w = 2
输出:3
解释:
上图展示了一种可行的矩形放置方案:
- 一个矩形的左下角在
(0, 0),右上角在(2, 2)。 - 一个矩形的左下角在
(3, 0),右上角在(5, 5)。 - 一个矩形的左下角在
(6, 0),右上角在(6, 6)。
示例 3:
输入:points = [[2,3],[1,2]], w = 0
输出:2
解释:
上图展示了一种可行的矩形放置方案:
- 一个矩形的左下角在
(1, 0),右上角在(1, 2)。 - 一个矩形的左下角在
(2, 0),右上角在(2, 3)。
提示:
1 <= points.length <= 105points[i].length == 20 <= xi == points[i][0] <= 1090 <= yi == points[i][1] <= 1090 <= w <= 109- 所有点坐标
(xi, yi)互不相同。
根据题目描述,我们不需要考虑矩形的高度,只需要考虑矩形的宽度。
我们可以将所有的点按照横坐标进行排序,用一个变量
接下来我们遍历所有的点,如果当前点的横坐标
遍历完成后,我们就得到了最少需要的矩形数目。
时间复杂度
class Solution:
def minRectanglesToCoverPoints(self, points: List[List[int]], w: int) -> int:
points.sort()
ans, x1 = 0, -1
for x, _ in points:
if x > x1:
ans += 1
x1 = x + w
return ansclass Solution {
public int minRectanglesToCoverPoints(int[][] points, int w) {
Arrays.sort(points, (a, b) -> a[0] - b[0]);
int ans = 0, x1 = -1;
for (int[] p : points) {
int x = p[0];
if (x > x1) {
++ans;
x1 = x + w;
}
}
return ans;
}
}class Solution {
public:
int minRectanglesToCoverPoints(vector<vector<int>>& points, int w) {
sort(points.begin(), points.end());
int ans = 0, x1 = -1;
for (const auto& p : points) {
int x = p[0];
if (x > x1) {
++ans;
x1 = x + w;
}
}
return ans;
}
};func minRectanglesToCoverPoints(points [][]int, w int) (ans int) {
sort.Slice(points, func(i, j int) bool { return points[i][0] < points[j][0] })
x1 := -1
for _, p := range points {
if x := p[0]; x > x1 {
ans++
x1 = x + w
}
}
return
}function minRectanglesToCoverPoints(points: number[][], w: number): number {
points.sort((a, b) => a[0] - b[0]);
let [ans, x1] = [0, -1];
for (const [x, _] of points) {
if (x > x1) {
++ans;
x1 = x + w;
}
}
return ans;
}impl Solution {
pub fn min_rectangles_to_cover_points(mut points: Vec<Vec<i32>>, w: i32) -> i32 {
points.sort_by(|a, b| a[0].cmp(&b[0]));
let mut ans = 0;
let mut x1 = -1;
for p in points {
let x = p[0];
if x > x1 {
ans += 1;
x1 = x + w;
}
}
ans
}
}public class Solution {
public int MinRectanglesToCoverPoints(int[][] points, int w) {
Array.Sort(points, (a, b) => a[0] - b[0]);
int ans = 0, x1 = -1;
foreach (int[] p in points) {
int x = p[0];
if (x > x1) {
ans++;
x1 = x + w;
}
}
return ans;
}
}