comments

difficulty

edit_url

545. 二叉树的边界 🔒

English Version

题目描述

二叉树的边界是由 根节点 、左边界 、按从左到右顺序的 叶节点 和 逆序的右边界 ，按顺序依次连接组成。

左边界 是满足下述定义的节点集合：

根节点的左子节点在左边界中。如果根节点不含左子节点，那么左边界就为空。
如果一个节点在左边界中，并且该节点有左子节点，那么它的左子节点也在左边界中。
如果一个节点在左边界中，并且该节点不含左子节点，那么它的右子节点就在左边界中。
最左侧的叶节点不在左边界中。

右边界 定义方式与 左边界 相同，只是将左替换成右。即，右边界是根节点右子树的右侧部分；叶节点不是右边界的组成部分；如果根节点不含右子节点，那么右边界为空。

叶节点 是没有任何子节点的节点。对于此问题，根节点不是叶节点。

给你一棵二叉树的根节点 root ，按顺序返回组成二叉树边界的这些值。

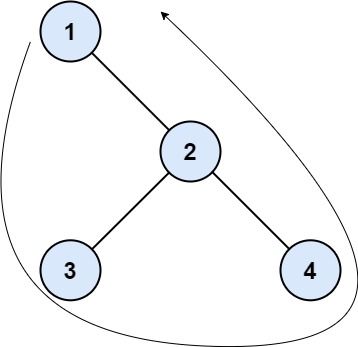
示例 1：

输入：root = [1,null,2,3,4]
输出：[1,3,4,2]
解释：
- 左边界为空，因为二叉树不含左子节点。
- 右边界是 [2] 。从根节点的右子节点开始的路径为 2 -> 4 ，但 4 是叶节点，所以右边界只有 2 。
- 叶节点从左到右是 [3,4] 。
按题目要求依序连接得到结果 [1] + [] + [3,4] + [2] = [1,3,4,2] 。

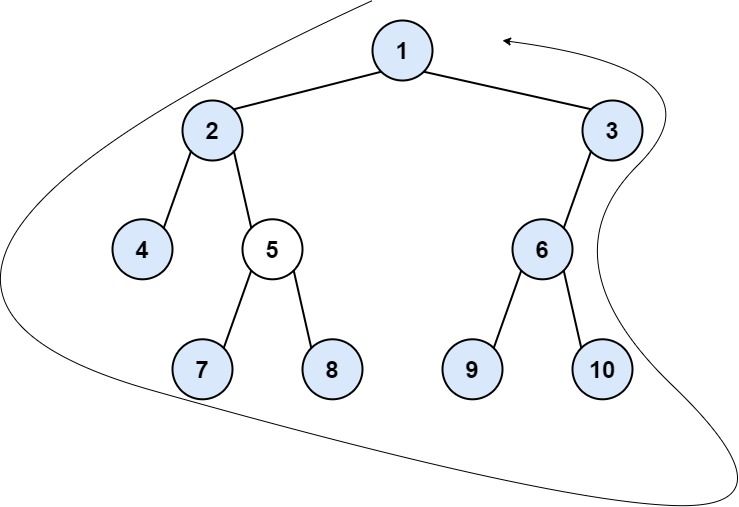
示例 2：

输入：root = [1,2,3,4,5,6,null,null,null,7,8,9,10]
输出：[1,2,4,7,8,9,10,6,3]
解释：
- 左边界为 [2] 。从根节点的左子节点开始的路径为 2 -> 4 ，但 4 是叶节点，所以左边界只有 2 。
- 右边界是 [3,6] ，逆序为 [6,3] 。从根节点的右子节点开始的路径为 3 -> 6 -> 10 ，但 10 是叶节点。
- 叶节点从左到右是 [4,7,8,9,10]
按题目要求依序连接得到结果 [1] + [2] + [4,7,8,9,10] + [6,3] = [1,2,4,7,8,9,10,6,3] 。

提示：

树中节点的数目在范围 [1, 10⁴] 内
-1000 <= Node.val <= 1000

解法

方法一：DFS

首先，如果树只有一个节点，那么直接返回这个节点的值的列表。

否则，我们可以通过深度优先搜索，找到二叉树的左边界、叶节点和右边界。

具体地，我们可以通过一个递归函数 $\textit{dfs}$ 来找到这三个部分。在 $\textit{dfs}$ 函数中，我们需要传入一个列表 $\textit{nums}$，一个节点 $\textit{root}$ 和一个整数 $\textit{i}$，其中 $\textit{nums}$ 用来存储当前部分的节点值，而 $\textit{root}$ 和 $\textit{i}$ 分别表示当前节点和当前部分的类型（左边界, 叶节点或右边界）。

函数的具体实现如下：

如果 $\textit{root}$ 为空，那么直接返回。
如果 $\textit{i} = 0$，那么我们需要找到左边界。如果 $\textit{root}$ 不是叶节点，那么我们将 $\textit{root}$ 的值加入到 $\textit{nums}$ 中。如果 $\textit{root}$ 有左子节点，那么我们递归地调用 $\textit{dfs}$ 函数，传入 $\textit{nums}$, $\textit{root}$ 的左子节点和 $\textit{i}$。否则，我们递归地调用 $\textit{dfs}$ 函数，传入 $\textit{nums}$, $\textit{root}$ 的右子节点和 $\textit{i}$。
如果 $\textit{i} = 1$，那么我们需要找到叶节点。如果 $\textit{root}$ 是叶节点，那么我们将 $\textit{root}$ 的值加入到 $\textit{nums}$ 中。否则，我们递归地调用 $\textit{dfs}$ 函数，传入 $\textit{nums}$, $\textit{root}$ 的左子节点和 $\textit{i}$，以及 $\textit{nums}$, $\textit{root}$ 的右子节点和 $\textit{i}$。
如果 $\textit{i} = 2$，那么我们需要找到右边界。如果 $\textit{root}$ 不是叶节点，那么我们将 $\textit{root}$ 的值加入到 $\textit{nums}$ 中，如果 $\textit{root}$ 有右子节点，那么我们递归地调用 $\textit{dfs}$ 函数，传入 $\textit{nums}$, $\textit{root}$ 的右子节点和 $\textit{i}$。否则，我们递归地调用 $\textit{dfs}$ 函数，传入 $\textit{nums}$, $\textit{root}$ 的左子节点和 $\textit{i}$。

我们分别调用 $\textit{dfs}$ 函数，找到左边界、叶节点和右边界，然后将这三个部分连接起来，即可得到答案。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def boundaryOfBinaryTree(self, root: Optional[TreeNode]) -> List[int]:
        def dfs(nums: List[int], root: Optional[TreeNode], i: int):
            if root is None:
                return
            if i == 0:
                if root.left != root.right:
                    nums.append(root.val)
                    if root.left:
                        dfs(nums, root.left, i)
                    else:
                        dfs(nums, root.right, i)
            elif i == 1:
                if root.left == root.right:
                    nums.append(root.val)
                else:
                    dfs(nums, root.left, i)
                    dfs(nums, root.right, i)
            else:
                if root.left != root.right:
                    nums.append(root.val)
                    if root.right:
                        dfs(nums, root.right, i)
                    else:
                        dfs(nums, root.left, i)

        ans = [root.val]
        if root.left == root.right:
            return ans
        left, leaves, right = [], [], []
        dfs(left, root.left, 0)
        dfs(leaves, root, 1)
        dfs(right, root.right, 2)
        ans += left + leaves + right[::-1]
        return ans

Java

class Solution {
    public List<Integer> boundaryOfBinaryTree(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        ans.add(root.val);
        if (root.left == root.right) {
            return ans;
        }
        List<Integer> left = new ArrayList<>();
        List<Integer> leaves = new ArrayList<>();
        List<Integer> right = new ArrayList<>();
        dfs(left, root.left, 0);
        dfs(leaves, root, 1);
        dfs(right, root.right, 2);

        ans.addAll(left);
        ans.addAll(leaves);
        Collections.reverse(right);
        ans.addAll(right);
        return ans;
    }

    private void dfs(List<Integer> nums, TreeNode root, int i) {
        if (root == null) {
            return;
        }
        if (i == 0) {
            if (root.left != root.right) {
                nums.add(root.val);
                if (root.left != null) {
                    dfs(nums, root.left, i);
                } else {
                    dfs(nums, root.right, i);
                }
            }
        } else if (i == 1) {
            if (root.left == root.right) {
                nums.add(root.val);
            } else {
                dfs(nums, root.left, i);
                dfs(nums, root.right, i);
            }
        } else {
            if (root.left != root.right) {
                nums.add(root.val);
                if (root.right != null) {
                    dfs(nums, root.right, i);
                } else {
                    dfs(nums, root.left, i);
                }
            }
        }
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> boundaryOfBinaryTree(TreeNode* root) {
        auto dfs = [&](this auto&& dfs, vector<int>& nums, TreeNode* root, int i) -> void {
            if (!root) {
                return;
            }
            if (i == 0) {
                if (root->left != root->right) {
                    nums.push_back(root->val);
                    if (root->left) {
                        dfs(nums, root->left, i);
                    } else {
                        dfs(nums, root->right, i);
                    }
                }
            } else if (i == 1) {
                if (root->left == root->right) {
                    nums.push_back(root->val);
                } else {
                    dfs(nums, root->left, i);
                    dfs(nums, root->right, i);
                }
            } else {
                if (root->left != root->right) {
                    nums.push_back(root->val);
                    if (root->right) {
                        dfs(nums, root->right, i);
                    } else {
                        dfs(nums, root->left, i);
                    }
                }
            }
        };
        vector<int> ans = {root->val};
        if (root->left == root->right) {
            return ans;
        }
        vector<int> left, right, leaves;
        dfs(left, root->left, 0);
        dfs(leaves, root, 1);
        dfs(right, root->right, 2);
        ans.insert(ans.end(), left.begin(), left.end());
        ans.insert(ans.end(), leaves.begin(), leaves.end());
        ans.insert(ans.end(), right.rbegin(), right.rend());
        return ans;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func boundaryOfBinaryTree(root *TreeNode) []int {
	ans := []int{root.Val}
	if root.Left == root.Right {
		return ans
	}

	left, leaves, right := []int{}, []int{}, []int{}

	var dfs func(nums *[]int, root *TreeNode, i int)
	dfs = func(nums *[]int, root *TreeNode, i int) {
		if root == nil {
			return
		}
		if i == 0 {
			if root.Left != root.Right {
				*nums = append(*nums, root.Val)
				if root.Left != nil {
					dfs(nums, root.Left, i)
				} else {
					dfs(nums, root.Right, i)
				}
			}
		} else if i == 1 {
			if root.Left == root.Right {
				*nums = append(*nums, root.Val)
			} else {
				dfs(nums, root.Left, i)
				dfs(nums, root.Right, i)
			}
		} else {
			if root.Left != root.Right {
				*nums = append(*nums, root.Val)
				if root.Right != nil {
					dfs(nums, root.Right, i)
				} else {
					dfs(nums, root.Left, i)
				}
			}
		}
	}

	dfs(&left, root.Left, 0)
	dfs(&leaves, root, 1)
	dfs(&right, root.Right, 2)

	ans = append(ans, left...)
	ans = append(ans, leaves...)
	for i := len(right) - 1; i >= 0; i-- {
		ans = append(ans, right[i])
	}

	return ans
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function boundaryOfBinaryTree(root: TreeNode | null): number[] {
    const ans: number[] = [root.val];
    if (root.left === root.right) {
        return ans;
    }

    const left: number[] = [];
    const leaves: number[] = [];
    const right: number[] = [];

    const dfs = function (nums: number[], root: TreeNode | null, i: number) {
        if (!root) {
            return;
        }
        if (i === 0) {
            if (root.left !== root.right) {
                nums.push(root.val);
                if (root.left) {
                    dfs(nums, root.left, i);
                } else {
                    dfs(nums, root.right, i);
                }
            }
        } else if (i === 1) {
            if (root.left === root.right) {
                nums.push(root.val);
            } else {
                dfs(nums, root.left, i);
                dfs(nums, root.right, i);
            }
        } else {
            if (root.left !== root.right) {
                nums.push(root.val);
                if (root.right) {
                    dfs(nums, root.right, i);
                } else {
                    dfs(nums, root.left, i);
                }
            }
        }
    };

    dfs(left, root.left, 0);
    dfs(leaves, root, 1);
    dfs(right, root.right, 2);

    return ans.concat(left).concat(leaves).concat(right.reverse());
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var boundaryOfBinaryTree = function (root) {
    const ans = [root.val];
    if (root.left === root.right) {
        return ans;
    }

    const left = [];
    const leaves = [];
    const right = [];

    const dfs = function (nums, root, i) {
        if (!root) {
            return;
        }
        if (i === 0) {
            if (root.left !== root.right) {
                nums.push(root.val);
                if (root.left) {
                    dfs(nums, root.left, i);
                } else {
                    dfs(nums, root.right, i);
                }
            }
        } else if (i === 1) {
            if (root.left === root.right) {
                nums.push(root.val);
            } else {
                dfs(nums, root.left, i);
                dfs(nums, root.right, i);
            }
        } else {
            if (root.left !== root.right) {
                nums.push(root.val);
                if (root.right) {
                    dfs(nums, root.right, i);
                } else {
                    dfs(nums, root.left, i);
                }
            }
        }
    };

    dfs(left, root.left, 0);
    dfs(leaves, root, 1);
    dfs(right, root.right, 2);
    return ans.concat(left).concat(leaves).concat(right.reverse());
};

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

545. 二叉树的边界 🔒

题目描述

解法

方法一：DFS

Python3

Java

C++

Go

TypeScript

JavaScript

Files

README.md

Latest commit

History

README.md

File metadata and controls

545. 二叉树的边界 🔒

题目描述

解法

方法一：DFS

Python3

Java

C++

Go

TypeScript

JavaScript