README.md

comments	difficulty	edit_url	rating	source	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3208.Alternating%20Groups%20II/README.md	1721	第 134 场双周赛 Q3	数组 滑动窗口

3208. 交替组 II

English Version

题目描述

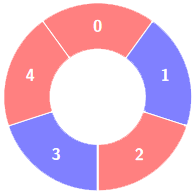
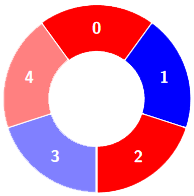
给你一个整数数组 colors 和一个整数 k ，colors表示一个由红色和蓝色瓷砖组成的环，第 i 块瓷砖的颜色为 colors[i] ：

• colors[i] == 0 表示第 i 块瓷砖的颜色是 红色 。
• colors[i] == 1 表示第 i 块瓷砖的颜色是 蓝色 。

环中连续 k 块瓷砖的颜色如果是 交替 颜色（也就是说除了第一块和最后一块瓷砖以外，中间瓷砖的颜色与它 左边 和 右边 的颜色都不同），那么它被称为一个 交替 组。

请你返回 交替 组的数目。

注意 ，由于 colors 表示一个 环 ，第一块 瓷砖和 最后一块 瓷砖是相邻的。

 

示例 1：

输入：colors = [0,1,0,1,0], k = 3

输出：3

解释：

交替组包括：

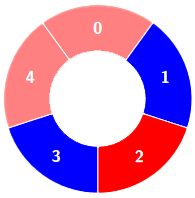
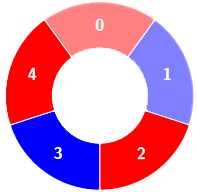
示例 2：

输入：colors = [0,1,0,0,1,0,1], k = 6

输出：2

解释：

交替组包括：

示例 3：

输入：colors = [1,1,0,1], k = 4

输出：0

解释：

 

提示：

• 3 <= colors.length <= 105
• 0 <= colors[i] <= 1
• 3 <= k <= colors.length

解法

方法一：一次遍历

我们可以将环展开成一个长度为 $2n$ 的数组，然后从左到右遍历这个数组，用一个变量 $\textit{cnt}$ 记录当前交替组的长度，如果遇到了相同的颜色，就将 $\textit{cnt}$ 重置为 $1$，否则将 $\textit{cnt}$ 加一。如果 $\textit{cnt} \ge k$，并且当前位置 $i$ 大于等于 $n$，那么就找到了一个交替组，答案加一。

遍历结束后，返回答案即可。

时间复杂度 $O(n)$，其中 $n$ 为数组 $\textit{colors}$ 的长度。空间复杂度 $O(1)$。

Python3

class Solution:
    def numberOfAlternatingGroups(self, colors: List[int], k: int) -> int:
        n = len(colors)
        ans = cnt = 0
        for i in range(n << 1):
            if i and colors[i % n] == colors[(i - 1) % n]:
                cnt = 1
            else:
                cnt += 1
            ans += i >= n and cnt >= k
        return ans

Java

class Solution {
    public int numberOfAlternatingGroups(int[] colors, int k) {
        int n = colors.length;
        int ans = 0, cnt = 0;
        for (int i = 0; i < n << 1; ++i) {
            if (i > 0 && colors[i % n] == colors[(i - 1) % n]) {
                cnt = 1;
            } else {
                ++cnt;
            }
            ans += i >= n && cnt >= k ? 1 : 0;
        }
        return ans;
    }
}

C++

class Solution {
public:
    int numberOfAlternatingGroups(vector<int>& colors, int k) {
        int n = colors.size();
        int ans = 0, cnt = 0;
        for (int i = 0; i < n << 1; ++i) {
            if (i && colors[i % n] == colors[(i - 1) % n]) {
                cnt = 1;
            } else {
                ++cnt;
            }
            ans += i >= n && cnt >= k ? 1 : 0;
        }
        return ans;
    }
};

Go

func numberOfAlternatingGroups(colors []int, k int) (ans int) {
	n := len(colors)
	cnt := 0
	for i := 0; i < n<<1; i++ {
		if i > 0 && colors[i%n] == colors[(i-1)%n] {
			cnt = 1
		} else {
			cnt++
		}
		if i >= n && cnt >= k {
			ans++
		}
	}
	return
}

TypeScript

function numberOfAlternatingGroups(colors: number[], k: number): number {
    const n = colors.length;
    let [ans, cnt] = [0, 0];
    for (let i = 0; i < n << 1; ++i) {
        if (i && colors[i % n] === colors[(i - 1) % n]) {
            cnt = 1;
        } else {
            ++cnt;
        }
        ans += i >= n && cnt >= k ? 1 : 0;
    }
    return ans;
}