Skip to content

Latest commit

 

History

History
242 lines (189 loc) · 7.07 KB

README_EN.md

File metadata and controls

242 lines (189 loc) · 7.07 KB
comments difficulty edit_url rating source tags
true
Medium
1430
Weekly Contest 370 Q2
Graph

2924. Find Champion II

中文文档

Description

There are n teams numbered from 0 to n - 1 in a tournament; each team is also a node in a DAG.

You are given the integer n and a 0-indexed 2D integer array edges of length m representing the DAG, where edges[i] = [ui, vi] indicates that there is a directed edge from team ui to team vi in the graph.

A directed edge from a to b in the graph means that team a is stronger than team b and team b is weaker than team a.

Team a will be the champion of the tournament if there is no team b that is stronger than team a.

Return the team that will be the champion of the tournament if there is a unique champion, otherwise, return -1.

Notes

  • A cycle is a series of nodes a1, a2, ..., an, an+1 such that node a1 is the same node as node an+1, the nodes a1, a2, ..., an are distinct, and there is a directed edge from the node ai to node ai+1 for every i in the range [1, n].
  • A DAG is a directed graph that does not have any cycle.

 

Example 1:

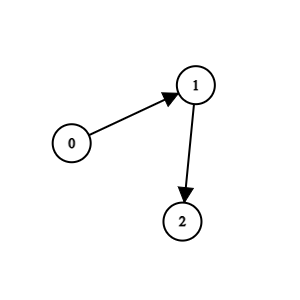
Input: n = 3, edges = [[0,1],[1,2]]
Output: 0
Explanation: Team 1 is weaker than team 0. Team 2 is weaker than team 1. So the champion is team 0.

Example 2:

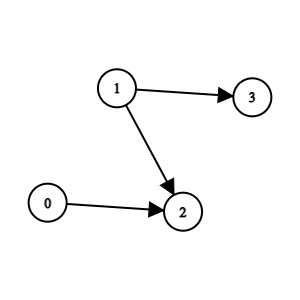
Input: n = 4, edges = [[0,2],[1,3],[1,2]]
Output: -1
Explanation: Team 2 is weaker than team 0 and team 1. Team 3 is weaker than team 1. But team 1 and team 0 are not weaker than any other teams. So the answer is -1.

 

Constraints:

  • 1 <= n <= 100
  • m == edges.length
  • 0 <= m <= n * (n - 1) / 2
  • edges[i].length == 2
  • 0 <= edge[i][j] <= n - 1
  • edges[i][0] != edges[i][1]
  • The input is generated such that if team a is stronger than team b, team b is not stronger than team a.
  • The input is generated such that if team a is stronger than team b and team b is stronger than team c, then team a is stronger than team c.

Solutions

Solution 1: Counting In-degrees

Based on the problem description, we only need to count the in-degrees of each node and record them in an array $indeg$. If only one node has an in-degree of $0$, then this node is the champion; otherwise, there is no unique champion.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.

Python3

class Solution:
    def findChampion(self, n: int, edges: List[List[int]]) -> int:
        indeg = [0] * n
        for _, v in edges:
            indeg[v] += 1
        return -1 if indeg.count(0) != 1 else indeg.index(0)

Java

class Solution {
    public int findChampion(int n, int[][] edges) {
        int[] indeg = new int[n];
        for (var e : edges) {
            ++indeg[e[1]];
        }
        int ans = -1, cnt = 0;
        for (int i = 0; i < n; ++i) {
            if (indeg[i] == 0) {
                ++cnt;
                ans = i;
            }
        }
        return cnt == 1 ? ans : -1;
    }
}

C++

class Solution {
public:
    int findChampion(int n, vector<vector<int>>& edges) {
        int indeg[n];
        memset(indeg, 0, sizeof(indeg));
        for (auto& e : edges) {
            ++indeg[e[1]];
        }
        int ans = -1, cnt = 0;
        for (int i = 0; i < n; ++i) {
            if (indeg[i] == 0) {
                ++cnt;
                ans = i;
            }
        }
        return cnt == 1 ? ans : -1;
    }
};

Go

func findChampion(n int, edges [][]int) int {
	indeg := make([]int, n)
	for _, e := range edges {
		indeg[e[1]]++
	}
	ans, cnt := -1, 0
	for i, x := range indeg {
		if x == 0 {
			cnt++
			ans = i
		}
	}
	if cnt == 1 {
		return ans
	}
	return -1
}

TypeScript

function findChampion(n: number, edges: number[][]): number {
    const indeg: number[] = Array(n).fill(0);
    for (const [_, v] of edges) {
        ++indeg[v];
    }
    let [ans, cnt] = [-1, 0];
    for (let i = 0; i < n; ++i) {
        if (indeg[i] === 0) {
            ++cnt;
            ans = i;
        }
    }
    return cnt === 1 ? ans : -1;
}

JavaScript

function findChampion(n, edges) {
    const indeg = Array(n).fill(0);
    for (const [_, v] of edges) {
        ++indeg[v];
    }
    let [ans, cnt] = [-1, 0];
    for (let i = 0; i < n; ++i) {
        if (indeg[i] === 0) {
            ++cnt;
            ans = i;
        }
    }
    return cnt === 1 ? ans : -1;
}

Solution 2

TypeScript

function findChampion(n: number, edges: number[][]): number {
    const vertexes = new Set<number>(Array.from({ length: n }, (_, i) => i));

    for (const [_, v] of edges) {
        vertexes.delete(v);
    }

    return vertexes.size === 1 ? vertexes[Symbol.iterator]().next().value! : -1;
}

JavaScript

function findChampion(n, edges) {
    const vertexes = new Set(Array.from({ length: n }, (_, i) => i));
    for (const [_, v] of edges) {
        vertexes.delete(v);
    }
    return vertexes.size === 1 ? vertexes[Symbol.iterator]().next().value : -1;
}