| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
中等 |
1496 |
第 79 场双周赛 Q3 |
|
给你一个整数 n ,表示一个国家里的城市数目。城市编号为 0 到 n - 1 。
给你一个二维整数数组 roads ,其中 roads[i] = [ai, bi] 表示城市 ai 和 bi 之间有一条 双向 道路。
你需要给每个城市安排一个从 1 到 n 之间的整数值,且每个值只能被使用 一次 。道路的 重要性 定义为这条道路连接的两座城市数值 之和 。
请你返回在最优安排下,所有道路重要性 之和 最大 为多少。
示例 1:
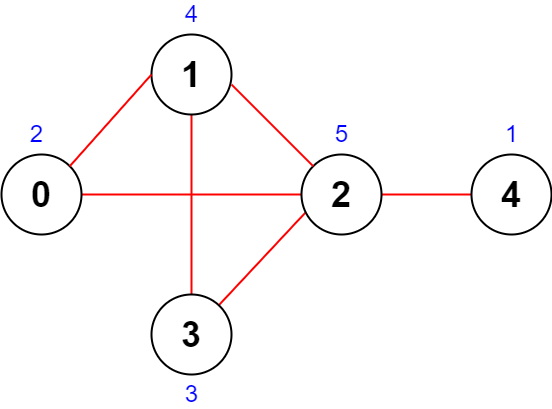
输入:n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]] 输出:43 解释:上图展示了国家图和每个城市被安排的值 [2,4,5,3,1] 。 - 道路 (0,1) 重要性为 2 + 4 = 6 。 - 道路 (1,2) 重要性为 4 + 5 = 9 。 - 道路 (2,3) 重要性为 5 + 3 = 8 。 - 道路 (0,2) 重要性为 2 + 5 = 7 。 - 道路 (1,3) 重要性为 4 + 3 = 7 。 - 道路 (2,4) 重要性为 5 + 1 = 6 。 所有道路重要性之和为 6 + 9 + 8 + 7 + 7 + 6 = 43 。 可以证明,重要性之和不可能超过 43 。
示例 2:
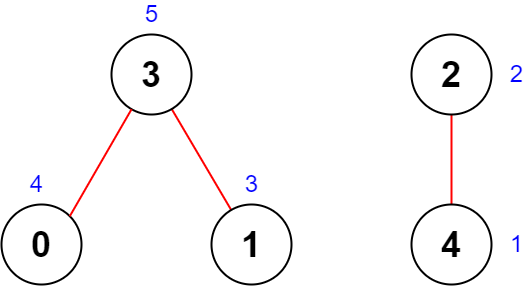
输入:n = 5, roads = [[0,3],[2,4],[1,3]] 输出:20 解释:上图展示了国家图和每个城市被安排的值 [4,3,2,5,1] 。 - 道路 (0,3) 重要性为 4 + 5 = 9 。 - 道路 (2,4) 重要性为 2 + 1 = 3 。 - 道路 (1,3) 重要性为 3 + 5 = 8 。 所有道路重要性之和为 9 + 3 + 8 = 20 。 可以证明,重要性之和不可能超过 20 。
提示:
2 <= n <= 5 * 1041 <= roads.length <= 5 * 104roads[i].length == 20 <= ai, bi <= n - 1ai != bi- 没有重复道路。
我们考虑每个城市对所有道路的总重要性的贡献度,记录在数组
时间复杂度
class Solution:
def maximumImportance(self, n: int, roads: List[List[int]]) -> int:
deg = [0] * n
for a, b in roads:
deg[a] += 1
deg[b] += 1
deg.sort()
return sum(i * v for i, v in enumerate(deg, 1))class Solution {
public long maximumImportance(int n, int[][] roads) {
int[] deg = new int[n];
for (int[] r : roads) {
++deg[r[0]];
++deg[r[1]];
}
Arrays.sort(deg);
long ans = 0;
for (int i = 0; i < n; ++i) {
ans += (long) (i + 1) * deg[i];
}
return ans;
}
}class Solution {
public:
long long maximumImportance(int n, vector<vector<int>>& roads) {
vector<int> deg(n);
for (auto& r : roads) {
++deg[r[0]];
++deg[r[1]];
}
sort(deg.begin(), deg.end());
long long ans = 0;
for (int i = 0; i < n; ++i) {
ans += (i + 1LL) * deg[i];
}
return ans;
}
};func maximumImportance(n int, roads [][]int) (ans int64) {
deg := make([]int, n)
for _, r := range roads {
deg[r[0]]++
deg[r[1]]++
}
sort.Ints(deg)
for i, x := range deg {
ans += int64(x) * int64(i+1)
}
return
}function maximumImportance(n: number, roads: number[][]): number {
const deg: number[] = Array(n).fill(0);
for (const [a, b] of roads) {
++deg[a];
++deg[b];
}
deg.sort((a, b) => a - b);
return deg.reduce((acc, cur, idx) => acc + (idx + 1) * cur, 0);
}