Skip to content

Latest commit

 

History

History
390 lines (343 loc) · 11.8 KB

README_EN.md

File metadata and controls

390 lines (343 loc) · 11.8 KB
comments difficulty edit_url rating source tags
true
Medium
1643
Weekly Contest 283 Q3
Tree
Array
Hash Table
Binary Tree

2196. Create Binary Tree From Descriptions

中文文档

Description

You are given a 2D integer array descriptions where descriptions[i] = [parenti, childi, isLefti] indicates that parenti is the parent of childi in a binary tree of unique values. Furthermore,

  • If isLefti == 1, then childi is the left child of parenti.
  • If isLefti == 0, then childi is the right child of parenti.

Construct the binary tree described by descriptions and return its root.

The test cases will be generated such that the binary tree is valid.

 

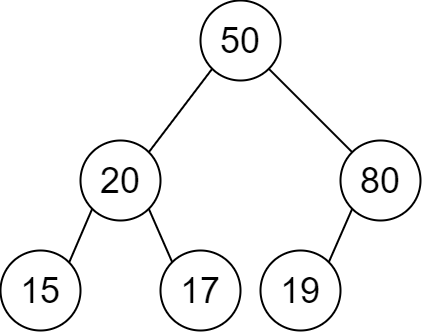
Example 1:

Input: descriptions = [[20,15,1],[20,17,0],[50,20,1],[50,80,0],[80,19,1]]
Output: [50,20,80,15,17,19]
Explanation: The root node is the node with value 50 since it has no parent.
The resulting binary tree is shown in the diagram.

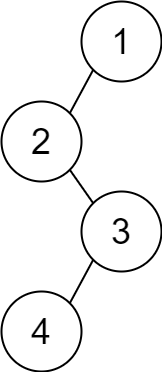
Example 2:

Input: descriptions = [[1,2,1],[2,3,0],[3,4,1]]
Output: [1,2,null,null,3,4]
Explanation: The root node is the node with value 1 since it has no parent.
The resulting binary tree is shown in the diagram.

 

Constraints:

  • 1 <= descriptions.length <= 104
  • descriptions[i].length == 3
  • 1 <= parenti, childi <= 105
  • 0 <= isLefti <= 1
  • The binary tree described by descriptions is valid.

Solutions

Solution 1: Hash Table

We can use a hash table $\textit{nodes}$ to store all nodes, where the keys are the values of the nodes, and the values are the nodes themselves. Additionally, we use a set $\textit{children}$ to store all child nodes.

We iterate through the $\textit{descriptions}$, and for each description $[\textit{parent}, \textit{child}, \textit{isLeft}]$, if $\textit{parent}$ is not in $\textit{nodes}$, we add $\textit{parent}$ to $\textit{nodes}$ and initialize a node with the value $\textit{parent}$. If $\textit{child}$ is not in $\textit{nodes}$, we add $\textit{child}$ to $\textit{nodes}$ and initialize a node with the value $\textit{child}$. Then, we add $\textit{child}$ to $\textit{children}$.

If $\textit{isLeft}$ is true, we set $\textit{child}$ as the left child of $\textit{parent}$; otherwise, we set $\textit{child}$ as the right child of $\textit{parent}$.

Finally, we iterate through $\textit{nodes}$, and if a node's value is not in $\textit{children}$, then this node is the root node, and we return this node.

The time complexity is $O(n)$, and the space complexity is $O(n)$, where $n$ is the length of $\textit{descriptions}$.

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def createBinaryTree(self, descriptions: List[List[int]]) -> Optional[TreeNode]:
        nodes = defaultdict(TreeNode)
        children = set()
        for parent, child, isLeft in descriptions:
            if parent not in nodes:
                nodes[parent] = TreeNode(parent)
            if child not in nodes:
                nodes[child] = TreeNode(child)
            children.add(child)
            if isLeft:
                nodes[parent].left = nodes[child]
            else:
                nodes[parent].right = nodes[child]
        root = (set(nodes.keys()) - children).pop()
        return nodes[root]

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode createBinaryTree(int[][] descriptions) {
        Map<Integer, TreeNode> nodes = new HashMap<>();
        Set<Integer> children = new HashSet<>();
        for (var d : descriptions) {
            int parent = d[0], child = d[1], isLeft = d[2];
            if (!nodes.containsKey(parent)) {
                nodes.put(parent, new TreeNode(parent));
            }
            if (!nodes.containsKey(child)) {
                nodes.put(child, new TreeNode(child));
            }
            if (isLeft == 1) {
                nodes.get(parent).left = nodes.get(child);
            } else {
                nodes.get(parent).right = nodes.get(child);
            }
            children.add(child);
        }
        for (var e : nodes.entrySet()) {
            if (!children.contains(e.getKey())) {
                return e.getValue();
            }
        }
        return null;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* createBinaryTree(vector<vector<int>>& descriptions) {
        unordered_map<int, TreeNode*> nodes;
        unordered_set<int> children;
        for (const auto& d : descriptions) {
            int parent = d[0], child = d[1], isLeft = d[2];
            if (!nodes.contains(parent)) {
                nodes[parent] = new TreeNode(parent);
            }
            if (!nodes.contains(child)) {
                nodes[child] = new TreeNode(child);
            }
            if (isLeft) {
                nodes[parent]->left = nodes[child];
            } else {
                nodes[parent]->right = nodes[child];
            }
            children.insert(child);
        }
        for (const auto& [k, v] : nodes) {
            if (!children.contains(k)) {
                return v;
            }
        }
        return nullptr;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func createBinaryTree(descriptions [][]int) *TreeNode {
	nodes := map[int]*TreeNode{}
	children := map[int]bool{}
	for _, d := range descriptions {
		parent, child, isLeft := d[0], d[1], d[2]
		if _, ok := nodes[parent]; !ok {
			nodes[parent] = &TreeNode{Val: parent}
		}
		if _, ok := nodes[child]; !ok {
			nodes[child] = &TreeNode{Val: child}
		}
		if isLeft == 1 {
			nodes[parent].Left = nodes[child]
		} else {
			nodes[parent].Right = nodes[child]
		}
		children[child] = true
	}
	for k, v := range nodes {
		if _, ok := children[k]; !ok {
			return v
		}
	}
	return nil
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function createBinaryTree(descriptions: number[][]): TreeNode | null {
    const nodes: Record<number, TreeNode> = {};
    const children = new Set<number>();
    for (const [parent, child, isLeft] of descriptions) {
        if (!nodes[parent]) {
            nodes[parent] = new TreeNode(parent);
        }
        if (!nodes[child]) {
            nodes[child] = new TreeNode(child);
        }
        if (isLeft) {
            nodes[parent].left = nodes[child];
        } else {
            nodes[parent].right = nodes[child];
        }
        children.add(child);
    }
    for (const [k, v] of Object.entries(nodes)) {
        if (!children.has(+k)) {
            return v;
        }
    }
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::collections::{HashMap, HashSet};
use std::rc::Rc;
impl Solution {
    pub fn create_binary_tree(descriptions: Vec<Vec<i32>>) -> Option<Rc<RefCell<TreeNode>>> {
        let mut nodes = HashMap::new();
        let mut children = HashSet::new();

        for d in descriptions {
            let parent = d[0];
            let child = d[1];
            let is_left = d[2];

            nodes
                .entry(parent)
                .or_insert_with(|| Rc::new(RefCell::new(TreeNode::new(parent))));
            nodes
                .entry(child)
                .or_insert_with(|| Rc::new(RefCell::new(TreeNode::new(child))));

            if is_left == 1 {
                nodes.get(&parent).unwrap().borrow_mut().left =
                    Some(Rc::clone(nodes.get(&child).unwrap()));
            } else {
                nodes.get(&parent).unwrap().borrow_mut().right =
                    Some(Rc::clone(nodes.get(&child).unwrap()));
            }

            children.insert(child);
        }

        for (key, node) in &nodes {
            if !children.contains(key) {
                return Some(Rc::clone(node));
            }
        }

        None
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[][]} descriptions
 * @return {TreeNode}
 */
var createBinaryTree = function (descriptions) {
    const nodes = {};
    const children = new Set();
    for (const [parent, child, isLeft] of descriptions) {
        if (!nodes[parent]) {
            nodes[parent] = new TreeNode(parent);
        }
        if (!nodes[child]) {
            nodes[child] = new TreeNode(child);
        }
        if (isLeft) {
            nodes[parent].left = nodes[child];
        } else {
            nodes[parent].right = nodes[child];
        }
        children.add(child);
    }
    for (const [k, v] of Object.entries(nodes)) {
        if (!children.has(+k)) {
            return v;
        }
    }
};