Skip to content

Latest commit

 

History

History
185 lines (143 loc) · 5.84 KB

README.md

File metadata and controls

185 lines (143 loc) · 5.84 KB
comments difficulty edit_url tags
true
中等
位运算
数组
数学
矩阵

2128. 通过翻转行或列来去除所有的 1 🔒

English Version

题目描述

给你一个大小为 m x n 的二进制矩阵 grid。

每次操作，你可以选择 任意 一行 或者 一列，然后将其中的所有值翻转（0 变成 1， 1变成 0）。

如果经过 任意次 操作，你能将矩阵中所有的 1 去除，那么返回 true；否则返回 false。

 

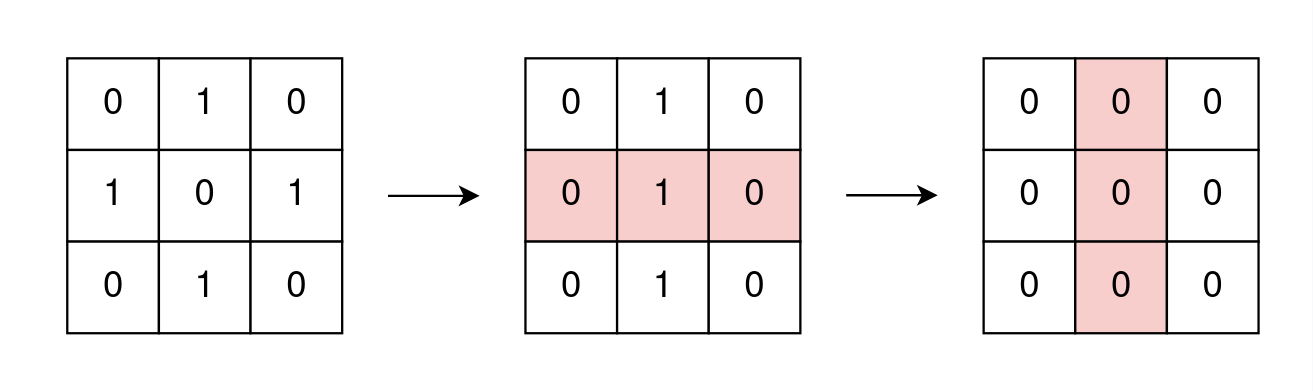
示例 1:

输入: grid = [[0,1,0],[1,0,1],[0,1,0]]
输出: true
解释: 一种去除所有 1 的可行方法是:
- 翻转矩阵的中间的行
- 翻转矩阵的中间的列

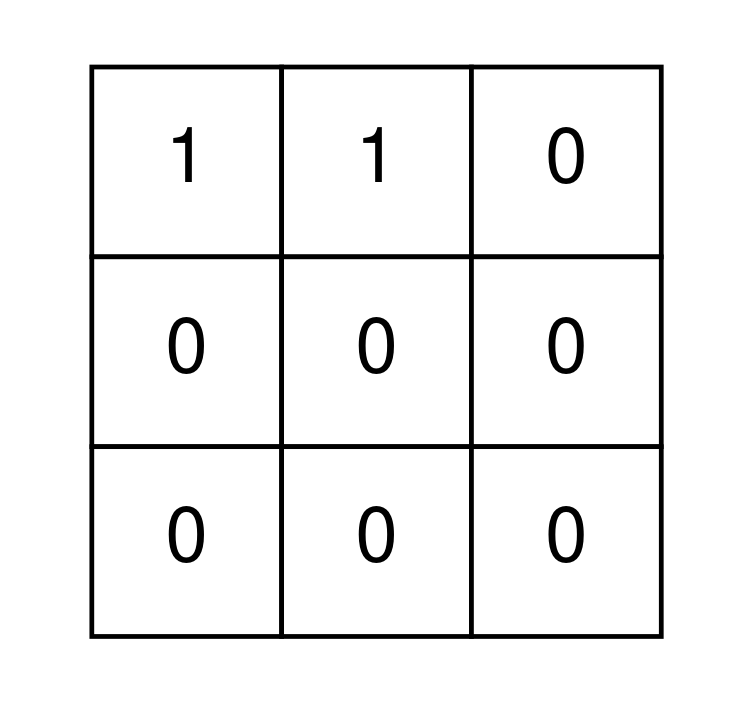
示例 2:

输入: grid = [[1,1,0],[0,0,0],[0,0,0]]
输出: false
解释: 不可能去除矩阵中所有的 1。

示例 3:

输入: grid = [[0]]
输出: true
解释: 矩阵中不存在 1，已经符合要求。

 

提示:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 300
  • grid[i][j] 是 0 或者 1.

解法

方法一：哈希表

我们观察发现，如果矩阵中的两行满足以下条件之一，则它们可以通过翻转某些列的方式得到相等的行：

  1. 两行的对应位置元素相等，即如果其中一行元素为 $1,0,0,1$，则另一行元素也为 $1,0,0,1$；
  2. 两行的对应位置元素相反，即如果其中一行元素为 $1,0,0,1$，则另一行元素为 $0,1,1,0$。

我们称满足以上条件之一的两行元素为“等价行”，那么题目所求的答案即为矩阵中最多包含等价行的行数。

因此，我们可以遍历矩阵的每一行，将每一行转换成第一个元素为 $0$ 的“等价行”。具体做法如下：

  • 如果当前行的第一个元素为 $0$，那么当前行的元素保持不变；
  • 如果当前行的第一个元素为 $1$，那么我们将当前行的每个元素进行翻转，即 $0$ 变成 $1$, $1$ 变成 $0$。也就是说，我们将以 $1$ 开头的行翻转成以 $0$ 开头的“等价行”。

这样一来，我们只需要用一个哈希表来统计转换后的每一行，如果最后哈希表只有一个元素，那么说明我们可以通过翻转行或列，将矩阵中所有的 $1$ 去除。

时间复杂度 $O(m \times n)$，空间复杂度 $O(m)$。其中 $m$ 和 $n$ 分别是矩阵的行数和列数。

相似题目：

Python3

class Solution:
    def removeOnes(self, grid: List[List[int]]) -> bool:
        s = set()
        for row in grid:
            t = tuple(row) if row[0] == grid[0][0] else tuple(x ^ 1 for x in row)
            s.add(t)
        return len(s) == 1

Java

class Solution {
    public boolean removeOnes(int[][] grid) {
        Set<String> s = new HashSet<>();
        int n = grid[0].length;
        for (var row : grid) {
            var cs = new char[n];
            for (int i = 0; i < n; ++i) {
                cs[i] = (char) (row[0] ^ row[i]);
            }
            s.add(String.valueOf(cs));
        }
        return s.size() == 1;
    }
}

C++

class Solution {
public:
    bool removeOnes(vector<vector<int>>& grid) {
        unordered_set<string> s;
        for (auto& row : grid) {
            string t;
            for (int x : row) {
                t.push_back('0' + (row[0] == 0 ? x : x ^ 1));
            }
            s.insert(t);
        }
        return s.size() == 1;
    }
};

Go

func removeOnes(grid [][]int) bool {
	s := map[string]bool{}
	for _, row := range grid {
		t := []byte{}
		for _, x := range row {
			if row[0] == 1 {
				x ^= 1
			}
			t = append(t, byte(x)+'0')
		}
		s[string(t)] = true
	}
	return len(s) == 1
}

TypeScript

function removeOnes(grid: number[][]): boolean {
    const s = new Set<string>();
    for (const row of grid) {
        if (row[0] === 1) {
            for (let i = 0; i < row.length; i++) {
                row[i] ^= 1;
            }
        }
        const t = row.join('');
        s.add(t);
    }
    return s.size === 1;
}