| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
困难 |
2104 |
第 66 场双周赛 Q4 |
|
有一个 矩形网格 状的农场,划分为 m 行 n 列的单元格。每个格子要么是 肥沃的 (用 1 表示),要么是 贫瘠 的(用 0 表示)。网格图以外的所有与格子都视为贫瘠的。
农场中的 金字塔 区域定义如下:
- 区域内格子数目 大于
1且所有格子都是 肥沃的 。 - 金字塔 顶端 是这个金字塔 最上方 的格子。金字塔的高度是它所覆盖的行数。令
(r, c)为金字塔的顶端且高度为h,那么金字塔区域内包含的任一格子(i, j)需满足r <= i <= r + h - 1且c - (i - r) <= j <= c + (i - r)。
一个 倒金字塔 类似定义如下:
- 区域内格子数目 大于
1且所有格子都是 肥沃的 。 - 倒金字塔的 顶端 是这个倒金字塔 最下方 的格子。倒金字塔的高度是它所覆盖的行数。令
(r, c)为金字塔的顶端且高度为h,那么金字塔区域内包含的任一格子(i, j)需满足r - h + 1 <= i <= r且c - (r - i) <= j <= c + (r - i)。
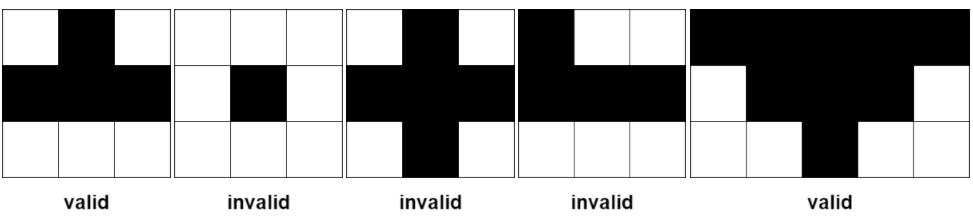
下图展示了部分符合定义和不符合定义的金字塔区域。黑色区域表示肥沃的格子。
给你一个下标从 0 开始且大小为 m x n 的二进制矩阵 grid ,它表示农场,请你返回 grid 中金字塔和倒金字塔的 总数目 。
示例 1:
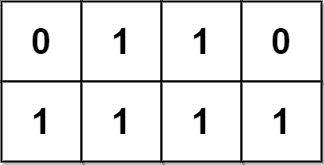
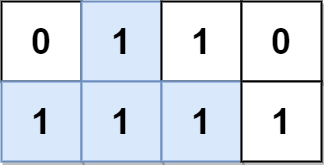
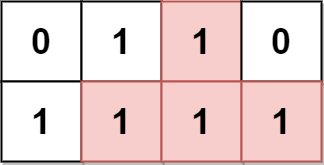
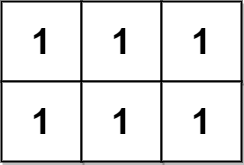
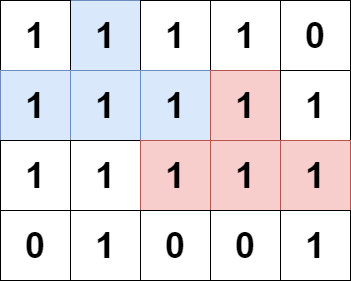
输入:grid = [[0,1,1,0],[1,1,1,1]] 输出:2 解释: 2 个可能的金字塔区域分别如上图蓝色和红色区域所示。 这个网格图中没有倒金字塔区域。 所以金字塔区域总数为 2 + 0 = 2 。
示例 2:
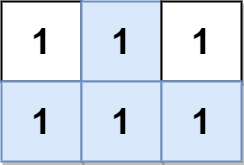
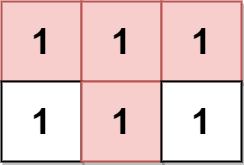
输入:grid = [[1,1,1],[1,1,1]] 输出:2 解释: 金字塔区域如上图蓝色区域所示,倒金字塔如上图红色区域所示。 所以金字塔区域总数目为 1 + 1 = 2 。
示例 3:
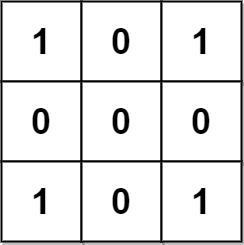
输入:grid = [[1,0,1],[0,0,0],[1,0,1]] 输出:0 解释: 网格图中没有任何金字塔或倒金字塔区域。
示例 4:
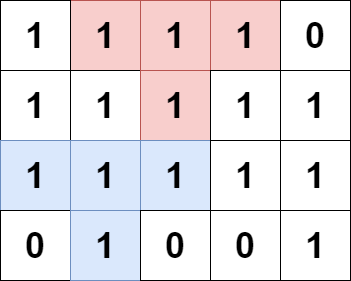
输入:grid = [[1,1,1,1,0],[1,1,1,1,1],[1,1,1,1,1],[0,1,0,0,1]] 输出:13 解释: 有 7 个金字塔区域。上图第二和第三张图中展示了它们中的 3 个。 有 6 个倒金字塔区域。上图中最后一张图展示了它们中的 2 个。 所以金字塔区域总数目为 7 + 6 = 13.
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 105grid[i][j]要么是0,要么是1。
我们定义
因此,我们可以从下往上、从左往右遍历网格,计算出所有的
接下来,我们考虑倒金字塔的个数。与金字塔类似,我们定义
因此,我们可以从上往下、从左往右遍历网格,计算出所有的
最后,正金字塔的个数加上倒金字塔的个数即为答案。实际代码中,我们可以只用一个二维数组
时间复杂度
class Solution:
def countPyramids(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
f = [[0] * n for _ in range(m)]
ans = 0
for i in range(m - 1, -1, -1):
for j in range(n):
if grid[i][j] == 0:
f[i][j] = -1
elif not (i == m - 1 or j == 0 or j == n - 1):
f[i][j] = min(f[i + 1][j - 1], f[i + 1][j], f[i + 1][j + 1]) + 1
ans += f[i][j]
for i in range(m):
for j in range(n):
if grid[i][j] == 0:
f[i][j] = -1
elif i == 0 or j == 0 or j == n - 1:
f[i][j] = 0
else:
f[i][j] = min(f[i - 1][j - 1], f[i - 1][j], f[i - 1][j + 1]) + 1
ans += f[i][j]
return ansclass Solution {
public int countPyramids(int[][] grid) {
int m = grid.length, n = grid[0].length;
int[][] f = new int[m][n];
int ans = 0;
for (int i = m - 1; i >= 0; --i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) {
f[i][j] = -1;
} else if (i == m - 1 || j == 0 || j == n - 1) {
f[i][j] = 0;
} else {
f[i][j] = Math.min(f[i + 1][j - 1], Math.min(f[i + 1][j], f[i + 1][j + 1])) + 1;
ans += f[i][j];
}
}
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) {
f[i][j] = -1;
} else if (i == 0 || j == 0 || j == n - 1) {
f[i][j] = 0;
} else {
f[i][j] = Math.min(f[i - 1][j - 1], Math.min(f[i - 1][j], f[i - 1][j + 1])) + 1;
ans += f[i][j];
}
}
}
return ans;
}
}class Solution {
public:
int countPyramids(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int f[m][n];
int ans = 0;
for (int i = m - 1; ~i; --i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) {
f[i][j] = -1;
} else if (i == m - 1 || j == 0 || j == n - 1) {
f[i][j] = 0;
} else {
f[i][j] = min({f[i + 1][j - 1], f[i + 1][j], f[i + 1][j + 1]}) + 1;
ans += f[i][j];
}
}
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) {
f[i][j] = -1;
} else if (i == 0 || j == 0 || j == n - 1) {
f[i][j] = 0;
} else {
f[i][j] = min({f[i - 1][j - 1], f[i - 1][j], f[i - 1][j + 1]}) + 1;
ans += f[i][j];
}
}
}
return ans;
}
};func countPyramids(grid [][]int) (ans int) {
m, n := len(grid), len(grid[0])
f := make([][]int, m)
for i := range f {
f[i] = make([]int, n)
}
for i := m - 1; i >= 0; i-- {
for j := 0; j < n; j++ {
if grid[i][j] == 0 {
f[i][j] = -1
} else if i == m-1 || j == 0 || j == n-1 {
f[i][j] = 0
} else {
f[i][j] = min(f[i+1][j-1], min(f[i+1][j], f[i+1][j+1])) + 1
ans += f[i][j]
}
}
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if grid[i][j] == 0 {
f[i][j] = -1
} else if i == 0 || j == 0 || j == n-1 {
f[i][j] = 0
} else {
f[i][j] = min(f[i-1][j-1], min(f[i-1][j], f[i-1][j+1])) + 1
ans += f[i][j]
}
}
}
return
}