Skip to content

Latest commit

 

History

History
383 lines (319 loc) · 8.94 KB

README_EN.md

File metadata and controls

383 lines (319 loc) · 8.94 KB
comments difficulty edit_url tags
true
Medium
Tree
Hash Table
Two Pointers
Binary Tree

1650. Lowest Common Ancestor of a Binary Tree III 🔒

中文文档

Description

Given two nodes of a binary tree p and q, return their lowest common ancestor (LCA).

Each node will have a reference to its parent node. The definition for Node is below:

class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

According to the definition of LCA on Wikipedia: "The lowest common ancestor of two nodes p and q in a tree T is the lowest node that has both p and q as descendants (where we allow a node to be a descendant of itself)."

 

Example 1:

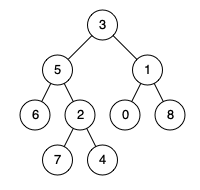
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5 since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [1,2], p = 1, q = 2
Output: 1

 

Constraints:

  • The number of nodes in the tree is in the range [2, 105].
  • -109 <= Node.val <= 109
  • All Node.val are unique.
  • p != q
  • p and q exist in the tree.

Solutions

Solution 1: Hash Table

We use a hash table $vis$ to record all nodes on the path from node $p$ to the root node. Then we start from node $q$ and traverse towards the root node. If we encounter a node that exists in the hash table $vis$, then this node is the nearest common ancestor of $p$ and $q$, and we can return it directly.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.

Python3

"""
# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None
"""


class Solution:
    def lowestCommonAncestor(self, p: "Node", q: "Node") -> "Node":
        vis = set()
        node = p
        while node:
            vis.add(node)
            node = node.parent
        node = q
        while node not in vis:
            node = node.parent
        return node

Java

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
};
*/

class Solution {
    public Node lowestCommonAncestor(Node p, Node q) {
        Set<Node> vis = new HashSet<>();
        for (Node node = p; node != null; node = node.parent) {
            vis.add(node);
        }
        for (Node node = q;; node = node.parent) {
            if (!vis.add(node)) {
                return node;
            }
        }
    }
}

C++

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* parent;
};
*/

class Solution {
public:
    Node* lowestCommonAncestor(Node* p, Node* q) {
        unordered_set<Node*> vis;
        for (Node* node = p; node; node = node->parent) {
            vis.insert(node);
        }
        for (Node* node = q;; node = node->parent) {
            if (vis.count(node)) {
                return node;
            }
        }
    }
};

Go

/**
 * Definition for Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Parent *Node
 * }
 */

func lowestCommonAncestor(p *Node, q *Node) *Node {
	vis := map[*Node]bool{}
	for node := p; node != nil; node = node.Parent {
		vis[node] = true
	}
	for node := q; ; node = node.Parent {
		if vis[node] {
			return node
		}
	}
}

TypeScript

/**
 * Definition for a binary tree node.
 * class Node {
 *     val: number
 *     left: Node | null
 *     right: Node | null
 *     parent: Node | null
 *     constructor(val?: number, left?: Node | null, right?: Node | null, parent?: Node | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *         this.parent = (parent===undefined ? null : parent)
 *     }
 * }
 */

function lowestCommonAncestor(p: Node | null, q: Node | null): Node | null {
    const vis: Set<Node> = new Set();
    for (let node = p; node; node = node.parent) {
        vis.add(node);
    }
    for (let node = q; ; node = node.parent) {
        if (vis.has(node)) {
            return node;
        }
    }
}

Solution 2: Two Pointers

We can use two pointers $a$ and $b$ to point to nodes $p$ and $q$ respectively, and then traverse towards the root node. When $a$ and $b$ meet, it is the nearest common ancestor of $p$ and $q$. Otherwise, if pointer $a$ traverses to the root node, then we let it point to node $q$, and do the same for pointer $b$. In this way, when the two pointers meet, it is the nearest common ancestor of $p$ and $q$.

The time complexity is $O(n)$, where $n$ is the number of nodes in the binary tree. The space complexity is $O(1)$.

Python3

"""
# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None
"""


class Solution:
    def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
        a, b = p, q
        while a != b:
            a = a.parent if a.parent else q
            b = b.parent if b.parent else p
        return a

Java

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
};
*/

class Solution {
    public Node lowestCommonAncestor(Node p, Node q) {
        Node a = p, b = q;
        while (a != b) {
            a = a.parent == null ? q : a.parent;
            b = b.parent == null ? p : b.parent;
        }
        return a;
    }
}

C++

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* parent;
};
*/

class Solution {
public:
    Node* lowestCommonAncestor(Node* p, Node* q) {
        Node* a = p;
        Node* b = q;
        while (a != b) {
            a = a->parent ? a->parent : q;
            b = b->parent ? b->parent : p;
        }
        return a;
    }
};

Go

/**
 * Definition for Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Parent *Node
 * }
 */

func lowestCommonAncestor(p *Node, q *Node) *Node {
	a, b := p, q
	for a != b {
		if a.Parent != nil {
			a = a.Parent
		} else {
			a = q
		}
		if b.Parent != nil {
			b = b.Parent
		} else {
			b = p
		}
	}
	return a
}

TypeScript

/**
 * Definition for a binary tree node.
 * class Node {
 *     val: number
 *     left: Node | null
 *     right: Node | null
 *     parent: Node | null
 *     constructor(val?: number, left?: Node | null, right?: Node | null, parent?: Node | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *         this.parent = (parent===undefined ? null : parent)
 *     }
 * }
 */

function lowestCommonAncestor(p: Node | null, q: Node | null): Node | null {
    let [a, b] = [p, q];
    while (a != b) {
        a = a.parent ?? q;
        b = b.parent ?? p;
    }
    return a;
}