| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
Medium |
1438 |
Weekly Contest 209 Q2 |
|
A binary tree is named Even-Odd if it meets the following conditions:
- The root of the binary tree is at level index
0, its children are at level index1, their children are at level index2, etc. - For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
- For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).
Given the root of a binary tree, return true if the binary tree is Even-Odd, otherwise return false.
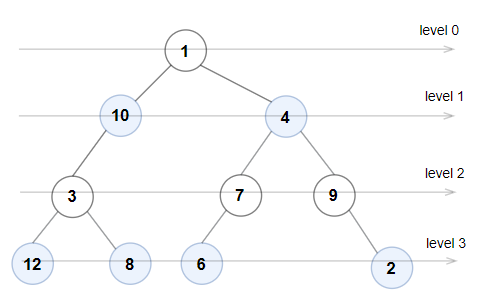
Example 1:
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2] Output: true Explanation: The node values on each level are: Level 0: [1] Level 1: [10,4] Level 2: [3,7,9] Level 3: [12,8,6,2] Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.
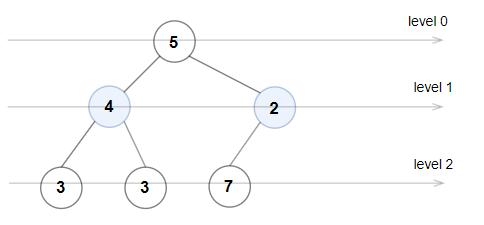
Example 2:
Input: root = [5,4,2,3,3,7] Output: false Explanation: The node values on each level are: Level 0: [5] Level 1: [4,2] Level 2: [3,3,7] Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.
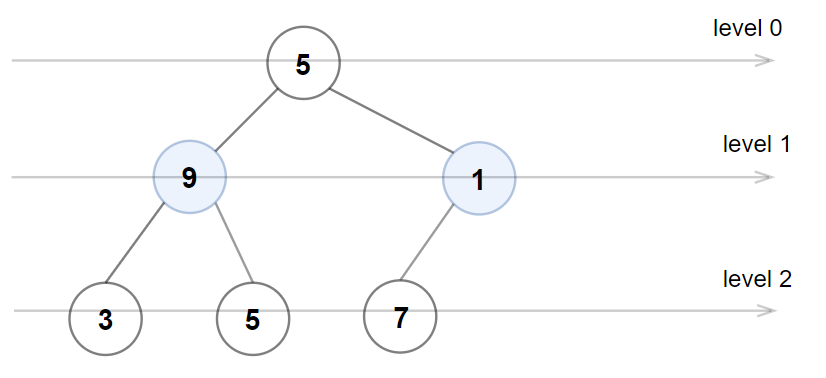
Example 3:
Input: root = [5,9,1,3,5,7] Output: false Explanation: Node values in the level 1 should be even integers.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 106
BFS traverses level by level. Each level is judged by its parity. The node values at each level are either all even or all odd, and they are strictly increasing or decreasing.
The time complexity is
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:
even = 1
q = deque([root])
while q:
prev = 0 if even else inf
for _ in range(len(q)):
root = q.popleft()
if even and (root.val % 2 == 0 or prev >= root.val):
return False
if not even and (root.val % 2 == 1 or prev <= root.val):
return False
prev = root.val
if root.left:
q.append(root.left)
if root.right:
q.append(root.right)
even ^= 1
return True/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isEvenOddTree(TreeNode root) {
boolean even = true;
Deque<TreeNode> q = new ArrayDeque<>();
q.offer(root);
while (!q.isEmpty()) {
int prev = even ? 0 : 1000001;
for (int n = q.size(); n > 0; --n) {
root = q.pollFirst();
if (even && (root.val % 2 == 0 || prev >= root.val)) {
return false;
}
if (!even && (root.val % 2 == 1 || prev <= root.val)) {
return false;
}
prev = root.val;
if (root.left != null) {
q.offer(root.left);
}
if (root.right != null) {
q.offer(root.right);
}
}
even = !even;
}
return true;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isEvenOddTree(TreeNode* root) {
int even = 1;
queue<TreeNode*> q{{root}};
while (!q.empty()) {
int prev = even ? 0 : 1e7;
for (int n = q.size(); n; --n) {
root = q.front();
q.pop();
if (even && (root->val % 2 == 0 || prev >= root->val)) {
return false;
}
if (!even && (root->val % 2 == 1 || prev <= root->val)) {
return false;
}
prev = root->val;
if (root->left) {
q.push(root->left);
}
if (root->right) {
q.push(root->right);
}
}
even ^= 1;
}
return true;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func isEvenOddTree(root *TreeNode) bool {
even := true
q := []*TreeNode{root}
for len(q) > 0 {
var prev int = 1e7
if even {
prev = 0
}
for n := len(q); n > 0; n-- {
root = q[0]
q = q[1:]
if even && (root.Val%2 == 0 || prev >= root.Val) {
return false
}
if !even && (root.Val%2 == 1 || prev <= root.Val) {
return false
}
prev = root.Val
if root.Left != nil {
q = append(q, root.Left)
}
if root.Right != nil {
q = append(q, root.Right)
}
}
even = !even
}
return true
}DFS performs a pre-order traversal of the binary tree, and similarly judges whether it meets the conditions based on the parity of the layer where the node is located. During the traversal, a hash table is used to record the node value that was most recently visited at each layer.
The time complexity is
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:
def dfs(root, i):
if root is None:
return True
even = i % 2 == 0
prev = d.get(i, 0 if even else inf)
if even and (root.val % 2 == 0 or prev >= root.val):
return False
if not even and (root.val % 2 == 1 or prev <= root.val):
return False
d[i] = root.val
return dfs(root.left, i + 1) and dfs(root.right, i + 1)
d = {}
return dfs(root, 0)/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private Map<Integer, Integer> d = new HashMap<>();
public boolean isEvenOddTree(TreeNode root) {
return dfs(root, 0);
}
private boolean dfs(TreeNode root, int i) {
if (root == null) {
return true;
}
boolean even = i % 2 == 0;
int prev = d.getOrDefault(i, even ? 0 : 1000001);
if (even && (root.val % 2 == 0 || prev >= root.val)) {
return false;
}
if (!even && (root.val % 2 == 1 || prev <= root.val)) {
return false;
}
d.put(i, root.val);
return dfs(root.left, i + 1) && dfs(root.right, i + 1);
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<int, int> d;
bool isEvenOddTree(TreeNode* root) {
return dfs(root, 0);
}
bool dfs(TreeNode* root, int i) {
if (!root) {
return true;
}
int even = i % 2 == 0;
int prev = d.count(i) ? d[i] : (even ? 0 : 1e7);
if (even && (root->val % 2 == 0 || prev >= root->val)) {
return false;
}
if (!even && (root->val % 2 == 1 || prev <= root->val)) {
return false;
}
d[i] = root->val;
return dfs(root->left, i + 1) && dfs(root->right, i + 1);
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func isEvenOddTree(root *TreeNode) bool {
d := map[int]int{}
var dfs func(*TreeNode, int) bool
dfs = func(root *TreeNode, i int) bool {
if root == nil {
return true
}
even := i%2 == 0
prev, ok := d[i]
if !ok {
if even {
prev = 0
} else {
prev = 10000000
}
}
if even && (root.Val%2 == 0 || prev >= root.Val) {
return false
}
if !even && (root.Val%2 == 1 || prev <= root.Val) {
return false
}
d[i] = root.Val
return dfs(root.Left, i+1) && dfs(root.Right, i+1)
}
return dfs(root, 0)
}