Skip to content

Latest commit

 

History

History
267 lines (222 loc) · 7.44 KB

README.md

File metadata and controls

267 lines (222 loc) · 7.44 KB
comments difficulty edit_url tags
true
简单
树
深度优先搜索
广度优先搜索
二叉树

1469. 寻找所有的独生节点 🔒

English Version

题目描述

二叉树中，如果一个节点是其父节点的唯一子节点，则称这样的节点为 “独生节点” 。二叉树的根节点不会是独生节点，因为它没有父节点。

给定一棵二叉树的根节点 root ，返回树中 所有的独生节点的值所构成的数组 。数组的顺序 不限 。

 

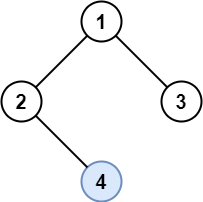
示例 1：

输入：root = [1,2,3,null,4]
输出：[4]
解释：浅蓝色的节点是唯一的独生节点。
节点 1 是根节点，不是独生的。
节点 2 和 3 有共同的父节点，所以它们都不是独生的。

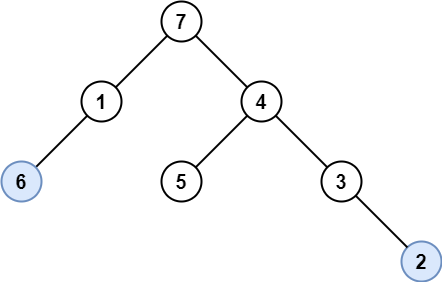
示例 2：

输入：root = [7,1,4,6,null,5,3,null,null,null,null,null,2]
输出：[6,2]
输出：浅蓝色的节点是独生节点。
请谨记，顺序是不限的。 [2,6] 也是一种可接受的答案。

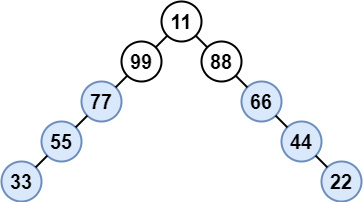
示例 3：

输入：root = [11,99,88,77,null,null,66,55,null,null,44,33,null,null,22]
输出：[77,55,33,66,44,22]
解释：节点 99 和 88 有共同的父节点，节点 11 是根节点。
其他所有节点都是独生节点。

 

提示：

  • tree 中节点个数的取值范围是 [1, 1000]。
  • 1 <= Node.val <= 106

解法

方法一：DFS

我们可以使用深度优先搜索遍历整棵树，设计一个函数 $\textit{dfs}$，它的作用是遍历树中的每个节点，如果当前节点是独生节点，那么将其值加入答案数组中。函数 $\textit{dfs}$ 的执行过程如下：

  1. 如果当前节点为空，或者当前节点是叶子节点，即当前节点的左右子节点都为空，那么直接返回。
  2. 如果当前节点的左子节点为空，那么将当前节点的右子节点是独生节点，将其值加入答案数组中。
  3. 如果当前节点的右子节点为空，那么将当前节点的左子节点是独生节点，将其值加入答案数组中。
  4. 递归遍历当前节点的左子节点和右子节点。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树中节点的个数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def getLonelyNodes(self, root: Optional[TreeNode]) -> List[int]:
        def dfs(root: Optional[TreeNode]):
            if root is None or root.left == root.right:
                return
            if root.left is None:
                ans.append(root.right.val)
            if root.right is None:
                ans.append(root.left.val)
            dfs(root.left)
            dfs(root.right)

        ans = []
        dfs(root)
        return ans

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private List<Integer> ans = new ArrayList<>();

    public List<Integer> getLonelyNodes(TreeNode root) {
        dfs(root);
        return ans;
    }

    private void dfs(TreeNode root) {
        if (root == null || (root.left == root.right)) {
            return;
        }
        if (root.left == null) {
            ans.add(root.right.val);
        }
        if (root.right == null) {
            ans.add(root.left.val);
        }
        dfs(root.left);
        dfs(root.right);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> getLonelyNodes(TreeNode* root) {
        vector<int> ans;
        auto dfs = [&](this auto&& dfs, TreeNode* root) {
            if (!root || (root->left == root->right)) {
                return;
            }
            if (!root->left) {
                ans.push_back(root->right->val);
            }
            if (!root->right) {
                ans.push_back(root->left->val);
            }
            dfs(root->left);
            dfs(root->right);
        };
        dfs(root);
        return ans;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
 func getLonelyNodes(root *TreeNode) (ans []int) {
	var dfs func(*TreeNode)
	dfs = func(root *TreeNode) {
		if root == nil || (root.Left == root.Right) {
			return
		}
		if root.Left == nil {
			ans = append(ans, root.Right.Val)
		}
		if root.Right == nil {
			ans = append(ans, root.Left.Val)
		}
		dfs(root.Left)
		dfs(root.Right)
	}
	dfs(root)
	return
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function getLonelyNodes(root: TreeNode | null): number[] {
    const ans: number[] = [];
    const dfs = (root: TreeNode | null) => {
        if (!root || root.left === root.right) {
            return;
        }
        if (!root.left) {
            ans.push(root.right.val);
        }
        if (!root.right) {
            ans.push(root.left.val);
        }
        dfs(root.left);
        dfs(root.right);
    };
    dfs(root);
    return ans;
}