README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/1300-1399/1329.Sort%20the%20Matrix%20Diagonally/README_EN.md	1548	Biweekly Contest 18 Q3	Array Matrix Sorting

1329. Sort the Matrix Diagonally

中文文档

Description

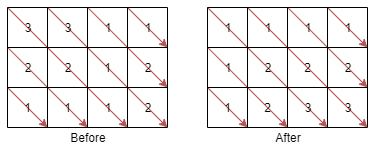
A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].

Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.

 

Example 1:

Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]

Example 2:

Input: mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
Output: [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• 1 <= mat[i][j] <= 100

Solutions

Solution 1: Sorting

We can treat each diagonal of the matrix as an array, sort these arrays, and then fill the sorted elements back into the original matrix.

Specifically, we denote the number of rows in the matrix as $m$ and the number of columns as $n$. Since any two elements $(i_1, j_1)$ and $(i_2, j_2)$ on the same diagonal satisfy $j_1 - i_1 = j_2 - i_2$, we can determine each diagonal based on the value of $j - i$. To ensure the value is positive, we add an offset $m$, that is, $m - i + j$.

Finally, we fill the sorted elements of each diagonal back into the original matrix.

The time complexity is $O(m \times n \times \log \min(m, n))$, and the space complexity is $O(m \times n)$. Where $m$ and $n$ are the number of rows and columns in the matrix, respectively.

Python3

class Solution:
    def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:
        m, n = len(mat), len(mat[0])
        g = [[] for _ in range(m + n)]
        for i, row in enumerate(mat):
            for j, x in enumerate(row):
                g[m - i + j].append(x)
        for e in g:
            e.sort(reverse=True)
        for i in range(m):
            for j in range(n):
                mat[i][j] = g[m - i + j].pop()
        return mat

Java

class Solution {
    public int[][] diagonalSort(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        List<Integer>[] g = new List[m + n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                g[m - i + j].add(mat[i][j]);
            }
        }
        for (var e : g) {
            Collections.sort(e, (a, b) -> b - a);
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                mat[i][j] = g[m - i + j].removeLast();
            }
        }
        return mat;
    }
}

C++

class Solution {
public:
    vector<vector<int>> diagonalSort(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<int> g[m + n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                g[m - i + j].push_back(mat[i][j]);
            }
        }
        for (auto& e : g) {
            sort(e.rbegin(), e.rend());
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                mat[i][j] = g[m - i + j].back();
                g[m - i + j].pop_back();
            }
        }
        return mat;
    }
};

Go

func diagonalSort(mat [][]int) [][]int {
	m, n := len(mat), len(mat[0])
	g := make([][]int, m+n)
	for i, row := range mat {
		for j, x := range row {
			g[m-i+j] = append(g[m-i+j], x)
		}
	}
	for _, e := range g {
		sort.Sort(sort.Reverse(sort.IntSlice(e)))
	}
	for i, row := range mat {
		for j := range row {
			k := len(g[m-i+j])
			mat[i][j] = g[m-i+j][k-1]
			g[m-i+j] = g[m-i+j][:k-1]
		}
	}
	return mat
}

TypeScript

function diagonalSort(mat: number[][]): number[][] {
    const [m, n] = [mat.length, mat[0].length];
    const g: number[][] = Array.from({ length: m + n }, () => []);
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            g[m - i + j].push(mat[i][j]);
        }
    }
    for (const e of g) {
        e.sort((a, b) => b - a);
    }
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            mat[i][j] = g[m - i + j].pop()!;
        }
    }
    return mat;
}

Rust

impl Solution {
    pub fn diagonal_sort(mut mat: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let m = mat.len();
        let n = mat[0].len();
        let mut g: Vec<Vec<i32>> = vec![vec![]; m + n];
        for i in 0..m {
            for j in 0..n {
                g[m - i + j].push(mat[i][j]);
            }
        }
        for e in &mut g {
            e.sort_by(|a, b| b.cmp(a));
        }
        for i in 0..m {
            for j in 0..n {
                mat[i][j] = g[m - i + j].pop().unwrap();
            }
        }
        mat
    }
}

C#

public class Solution {
    public int[][] DiagonalSort(int[][] mat) {
        int m = mat.Length;
        int n = mat[0].Length;
        List<List<int>> g = new List<List<int>>();
        for (int i = 0; i < m + n; i++) {
            g.Add(new List<int>());
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                g[m - i + j].Add(mat[i][j]);
            }
        }
        foreach (var e in g) {
            e.Sort((a, b) => b.CompareTo(a));
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int val = g[m - i + j][g[m - i + j].Count - 1];
                g[m - i + j].RemoveAt(g[m - i + j].Count - 1);
                mat[i][j] = val;
            }
        }
        return mat;
    }
}