Skip to content

Latest commit

 

History

History
201 lines (158 loc) · 5.47 KB

README_EN.md

File metadata and controls

201 lines (158 loc) · 5.47 KB
comments difficulty edit_url rating source tags
true
Easy
1302
Weekly Contest 164 Q1
Geometry
Array
Math

1266. Minimum Time Visiting All Points

中文文档

Description

On a 2D plane, there are n points with integer coordinates points[i] = [xi, yi]. Return the minimum time in seconds to visit all the points in the order given by points.

You can move according to these rules:

  • In 1 second, you can either: 
    <ul>
	<li>move vertically by one&nbsp;unit,</li>
	<li>move horizontally by one unit, or</li>
	<li>move diagonally <code>sqrt(2)</code> units (in other words, move one unit vertically then one unit horizontally in <code>1</code> second).</li>
</ul>
</li>
<li>You have to visit the points in the same order as they appear in the array.</li>
<li>You are allowed to pass through points that appear later in the order, but these do not count as visits.</li>

 

Example 1:

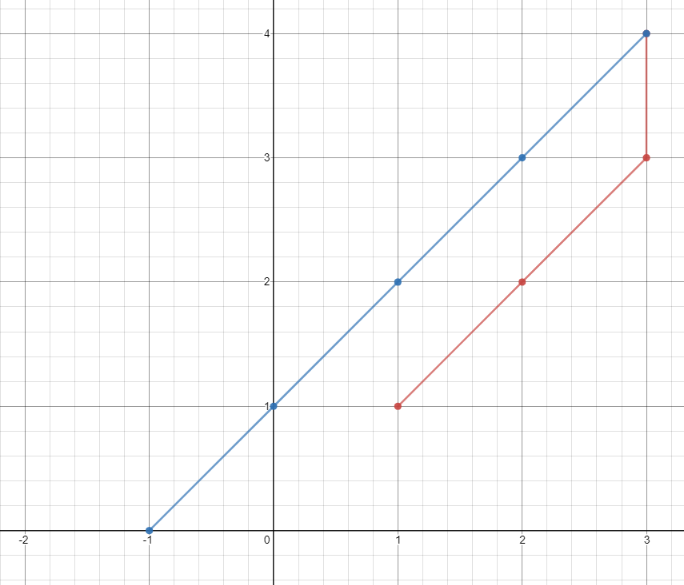
Input: points = [[1,1],[3,4],[-1,0]]
Output: 7
Explanation: One optimal path is [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]   
Time from [1,1] to [3,4] = 3 seconds 
Time from [3,4] to [-1,0] = 4 seconds
Total time = 7 seconds

Example 2:

Input: points = [[3,2],[-2,2]]
Output: 5

 

Constraints:

  • points.length == n
  • 1 <= n <= 100
  • points[i].length == 2
  • -1000 <= points[i][0], points[i][1] <= 1000

Solutions

Solution 1: Simulation

For two points $p1=(x_1, y_1)$ and $p2=(x_2, y_2)$, the distances moved in the x-axis and y-axis are $dx = |x_1 - x_2|$ and $dy = |y_1 - y_2|$ respectively.

If $dx \ge dy$, move along the diagonal for $dy$ steps, then move horizontally for $dx - dy$ steps. If $dx &lt; dy$, move along the diagonal for $dx$ steps, then move vertically for $dy - dx$ steps. Therefore, the minimum distance between the two points is $max(dx, dy)$.

We can iterate through all pairs of points, calculate the minimum distance between each pair of points, and then sum them up.

The time complexity is $O(n)$, where $n$ is the number of points. The space complexity is $O(1)$.

Python3

class Solution:
    def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:
        return sum(
            max(abs(p1[0] - p2[0]), abs(p1[1] - p2[1])) for p1, p2 in pairwise(points)
        )

Java

class Solution {
    public int minTimeToVisitAllPoints(int[][] points) {
        int ans = 0;
        for (int i = 1; i < points.length; ++i) {
            int dx = Math.abs(points[i][0] - points[i - 1][0]);
            int dy = Math.abs(points[i][1] - points[i - 1][1]);
            ans += Math.max(dx, dy);
        }
        return ans;
    }
}

C++

class Solution {
public:
    int minTimeToVisitAllPoints(vector<vector<int>>& points) {
        int ans = 0;
        for (int i = 1; i < points.size(); ++i) {
            int dx = abs(points[i][0] - points[i - 1][0]);
            int dy = abs(points[i][1] - points[i - 1][1]);
            ans += max(dx, dy);
        }
        return ans;
    }
};

Go

func minTimeToVisitAllPoints(points [][]int) (ans int) {
	for i, p := range points[1:] {
		dx := abs(p[0] - points[i][0])
		dy := abs(p[1] - points[i][1])
		ans += max(dx, dy)
	}
	return
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

TypeScript

function minTimeToVisitAllPoints(points: number[][]): number {
    let ans = 0;
    for (let i = 1; i < points.length; i++) {
        let dx = Math.abs(points[i][0] - points[i - 1][0]),
            dy = Math.abs(points[i][1] - points[i - 1][1]);
        ans += Math.max(dx, dy);
    }
    return ans;
}

Rust

impl Solution {
    pub fn min_time_to_visit_all_points(points: Vec<Vec<i32>>) -> i32 {
        let n = points.len();
        let mut ans = 0;
        for i in 1..n {
            let x = (points[i - 1][0] - points[i][0]).abs();
            let y = (points[i - 1][1] - points[i][1]).abs();
            ans += x.max(y);
        }
        ans
    }
}

C

#define max(a, b) (((a) > (b)) ? (a) : (b))

int minTimeToVisitAllPoints(int** points, int pointsSize, int* pointsColSize) {
    int ans = 0;
    for (int i = 1; i < pointsSize; i++) {
        int x = abs(points[i - 1][0] - points[i][0]);
        int y = abs(points[i - 1][1] - points[i][1]);
        ans += max(x, y);
    }
    return ans;
}