| comments | difficulty | edit_url | rating | source | tags | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
true |
Medium |
1439 |
Weekly Contest 163 Q2 |
|
Given a binary tree with the following rules:
root.val == 0- If
treeNode.val == xandtreeNode.left != null, thentreeNode.left.val == 2 * x + 1 - If
treeNode.val == xandtreeNode.right != null, thentreeNode.right.val == 2 * x + 2
Now the binary tree is contaminated, which means all treeNode.val have been changed to -1.
Implement the FindElements class:
FindElements(TreeNode* root)Initializes the object with a contaminated binary tree and recovers it.bool find(int target)Returnstrueif thetargetvalue exists in the recovered binary tree.
Example 1:
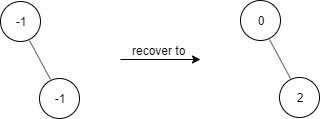
Input ["FindElements","find","find"] [[[-1,null,-1]],[1],[2]] Output [null,false,true] Explanation FindElements findElements = new FindElements([-1,null,-1]); findElements.find(1); // return False findElements.find(2); // return True
Example 2:
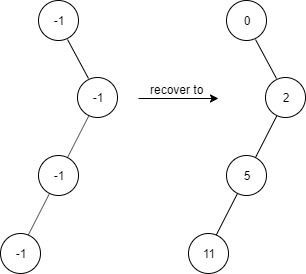
Input ["FindElements","find","find","find"] [[[-1,-1,-1,-1,-1]],[1],[3],[5]] Output [null,true,true,false] Explanation FindElements findElements = new FindElements([-1,-1,-1,-1,-1]); findElements.find(1); // return True findElements.find(3); // return True findElements.find(5); // return False
Example 3:
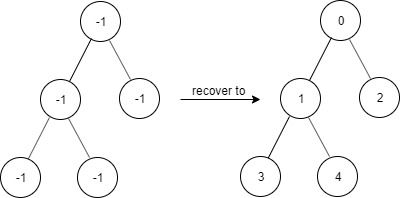
Input ["FindElements","find","find","find","find"] [[[-1,null,-1,-1,null,-1]],[2],[3],[4],[5]] Output [null,true,false,false,true] Explanation FindElements findElements = new FindElements([-1,null,-1,-1,null,-1]); findElements.find(2); // return True findElements.find(3); // return False findElements.find(4); // return False findElements.find(5); // return True
Constraints:
TreeNode.val == -1- The height of the binary tree is less than or equal to
20 - The total number of nodes is between
[1, 104] - Total calls of
find()is between[1, 104] 0 <= target <= 106
First, we traverse the binary tree using DFS, restore the node values to their original values, and store all node values in a hash table. Then, when searching, we only need to check if the target value exists in the hash table.
In terms of time complexity, it takes
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class FindElements:
def __init__(self, root: Optional[TreeNode]):
def dfs(root: Optional[TreeNode]):
self.s.add(root.val)
if root.left:
root.left.val = root.val * 2 + 1
dfs(root.left)
if root.right:
root.right.val = root.val * 2 + 2
dfs(root.right)
root.val = 0
self.s = set()
dfs(root)
def find(self, target: int) -> bool:
return target in self.s
# Your FindElements object will be instantiated and called as such:
# obj = FindElements(root)
# param_1 = obj.find(target)/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements {
private Set<Integer> s = new HashSet<>();
public FindElements(TreeNode root) {
root.val = 0;
dfs(root);
}
public boolean find(int target) {
return s.contains(target);
}
private void dfs(TreeNode root) {
s.add(root.val);
if (root.left != null) {
root.left.val = root.val * 2 + 1;
dfs(root.left);
}
if (root.right != null) {
root.right.val = root.val * 2 + 2;
dfs(root.right);
}
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*//**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements {
public:
FindElements(TreeNode* root) {
root->val = 0;
dfs(root);
}
bool find(int target) {
return s.contains(target);
}
private:
unordered_set<int> s;
void dfs(TreeNode* root) {
s.insert(root->val);
if (root->left) {
root->left->val = root->val * 2 + 1;
dfs(root->left);
}
if (root->right) {
root->right->val = root->val * 2 + 2;
dfs(root->right);
}
};
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*//**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
type FindElements struct {
s map[int]bool
}
func Constructor(root *TreeNode) FindElements {
root.Val = 0
s := map[int]bool{}
var dfs func(*TreeNode)
dfs = func(root *TreeNode) {
s[root.Val] = true
if root.Left != nil {
root.Left.Val = root.Val*2 + 1
dfs(root.Left)
}
if root.Right != nil {
root.Right.Val = root.Val*2 + 2
dfs(root.Right)
}
}
dfs(root)
return FindElements{s}
}
func (this *FindElements) Find(target int) bool {
return this.s[target]
}
/**
* Your FindElements object will be instantiated and called as such:
* obj := Constructor(root);
* param_1 := obj.Find(target);
*//**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
class FindElements {
private s: Set<number> = new Set<number>();
constructor(root: TreeNode | null) {
root.val = 0;
const dfs = (root: TreeNode) => {
this.s.add(root.val);
if (root.left) {
root.left.val = root.val * 2 + 1;
dfs(root.left);
}
if (root.right) {
root.right.val = root.val * 2 + 2;
dfs(root.right);
}
};
dfs(root);
}
find(target: number): boolean {
return this.s.has(target);
}
}
/**
* Your FindElements object will be instantiated and called as such:
* var obj = new FindElements(root)
* var param_1 = obj.find(target)
*/