| comments | difficulty | edit_url | rating | source | tags | ||
|---|---|---|---|---|---|---|---|
true |
Medium |
1710 |
Biweekly Contest 5 Q4 |
|
You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei.
In one semester, you can take any number of courses as long as you have taken all the prerequisites in the previous semester for the courses you are taking.
Return the minimum number of semesters needed to take all courses. If there is no way to take all the courses, return -1.
Example 1:
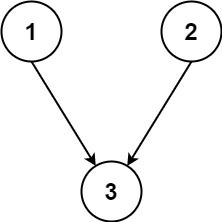
Input: n = 3, relations = [[1,3],[2,3]] Output: 2 Explanation: The figure above represents the given graph. In the first semester, you can take courses 1 and 2. In the second semester, you can take course 3.
Example 2:
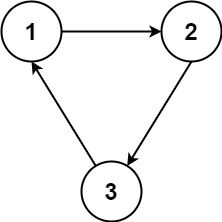
Input: n = 3, relations = [[1,2],[2,3],[3,1]] Output: -1 Explanation: No course can be studied because they are prerequisites of each other.
Constraints:
1 <= n <= 50001 <= relations.length <= 5000relations[i].length == 21 <= prevCoursei, nextCoursei <= nprevCoursei != nextCoursei- All the pairs
[prevCoursei, nextCoursei]are unique.
We can first build a graph
Then we enqueue the courses with an in-degree of
The time complexity is
class Solution:
def minimumSemesters(self, n: int, relations: List[List[int]]) -> int:
g = defaultdict(list)
indeg = [0] * n
for prev, nxt in relations:
prev, nxt = prev - 1, nxt - 1
g[prev].append(nxt)
indeg[nxt] += 1
q = deque(i for i, v in enumerate(indeg) if v == 0)
ans = 0
while q:
ans += 1
for _ in range(len(q)):
i = q.popleft()
n -= 1
for j in g[i]:
indeg[j] -= 1
if indeg[j] == 0:
q.append(j)
return -1 if n else ansclass Solution {
public int minimumSemesters(int n, int[][] relations) {
List<Integer>[] g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
int[] indeg = new int[n];
for (var r : relations) {
int prev = r[0] - 1, nxt = r[1] - 1;
g[prev].add(nxt);
++indeg[nxt];
}
Deque<Integer> q = new ArrayDeque<>();
for (int i = 0; i < n; ++i) {
if (indeg[i] == 0) {
q.offer(i);
}
}
int ans = 0;
while (!q.isEmpty()) {
++ans;
for (int k = q.size(); k > 0; --k) {
int i = q.poll();
--n;
for (int j : g[i]) {
if (--indeg[j] == 0) {
q.offer(j);
}
}
}
}
return n == 0 ? ans : -1;
}
}class Solution {
public:
int minimumSemesters(int n, vector<vector<int>>& relations) {
vector<vector<int>> g(n);
vector<int> indeg(n);
for (auto& r : relations) {
int prev = r[0] - 1, nxt = r[1] - 1;
g[prev].push_back(nxt);
++indeg[nxt];
}
queue<int> q;
for (int i = 0; i < n; ++i) {
if (indeg[i] == 0) {
q.push(i);
}
}
int ans = 0;
while (!q.empty()) {
++ans;
for (int k = q.size(); k; --k) {
int i = q.front();
q.pop();
--n;
for (int& j : g[i]) {
if (--indeg[j] == 0) {
q.push(j);
}
}
}
}
return n == 0 ? ans : -1;
}
};func minimumSemesters(n int, relations [][]int) (ans int) {
g := make([][]int, n)
indeg := make([]int, n)
for _, r := range relations {
prev, nxt := r[0]-1, r[1]-1
g[prev] = append(g[prev], nxt)
indeg[nxt]++
}
q := []int{}
for i, v := range indeg {
if v == 0 {
q = append(q, i)
}
}
for len(q) > 0 {
ans++
for k := len(q); k > 0; k-- {
i := q[0]
q = q[1:]
n--
for _, j := range g[i] {
indeg[j]--
if indeg[j] == 0 {
q = append(q, j)
}
}
}
}
if n == 0 {
return
}
return -1
}function minimumSemesters(n: number, relations: number[][]): number {
const g: number[][] = Array.from({ length: n }, () => []);
const indeg = new Array(n).fill(0);
for (const [prev, nxt] of relations) {
g[prev - 1].push(nxt - 1);
indeg[nxt - 1]++;
}
const q: number[] = [];
for (let i = 0; i < n; ++i) {
if (indeg[i] === 0) {
q.push(i);
}
}
let ans = 0;
while (q.length) {
++ans;
for (let k = q.length; k; --k) {
const i = q.shift()!;
--n;
for (const j of g[i]) {
if (--indeg[j] === 0) {
q.push(j);
}
}
}
}
return n === 0 ? ans : -1;
}