| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
Hard |
|
You are given the root of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor its parent, itself, and its immediate children.
Return the minimum number of cameras needed to monitor all nodes of the tree.
Example 1:
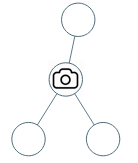
Input: root = [0,0,null,0,0] Output: 1 Explanation: One camera is enough to monitor all nodes if placed as shown.
Example 2:
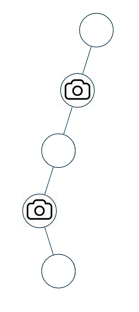
Input: root = [0,0,null,0,null,0,null,null,0] Output: 2 Explanation: At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. Node.val == 0
For each node, we define three states:
a: The current node has a camerab: The current node does not have a camera, but is monitored by its childrenc: The current node does not have a camera and is not monitored by its children
Next, we design a function root for the three states. The answer is
The calculation process of the function
If root is null, return inf represents a very large number, used to indicate an impossible situation.
Otherwise, we recursively calculate the left and right subtrees of root, obtaining
- If the current node has a camera, then its left and right children must be in a monitored state, i.e.,
$a = \min(la, lb, lc) + \min(ra, rb, rc) + 1$ . - If the current node does not have a camera but is monitored by its children, then one or both of the children must have a camera, i.e.,
$b = \min(la + rb, lb + ra, la + ra)$ . - If the current node does not have a camera and is not monitored by its children, then the children must be monitored by their children, i.e.,
$c = lb + rb$ .
Finally, we return
The time complexity is
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minCameraCover(self, root: Optional[TreeNode]) -> int:
def dfs(root):
if root is None:
return inf, 0, 0
la, lb, lc = dfs(root.left)
ra, rb, rc = dfs(root.right)
a = min(la, lb, lc) + min(ra, rb, rc) + 1
b = min(la + rb, lb + ra, la + ra)
c = lb + rb
return a, b, c
a, b, _ = dfs(root)
return min(a, b)/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int minCameraCover(TreeNode root) {
int[] ans = dfs(root);
return Math.min(ans[0], ans[1]);
}
private int[] dfs(TreeNode root) {
if (root == null) {
return new int[] {1 << 29, 0, 0};
}
var l = dfs(root.left);
var r = dfs(root.right);
int a = 1 + Math.min(Math.min(l[0], l[1]), l[2]) + Math.min(Math.min(r[0], r[1]), r[2]);
int b = Math.min(Math.min(l[0] + r[1], l[1] + r[0]), l[0] + r[0]);
int c = l[1] + r[1];
return new int[] {a, b, c};
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
struct Status {
int a, b, c;
};
class Solution {
public:
int minCameraCover(TreeNode* root) {
auto [a, b, _] = dfs(root);
return min(a, b);
}
Status dfs(TreeNode* root) {
if (!root) {
return {1 << 29, 0, 0};
}
auto [la, lb, lc] = dfs(root->left);
auto [ra, rb, rc] = dfs(root->right);
int a = 1 + min({la, lb, lc}) + min({ra, rb, rc});
int b = min({la + ra, la + rb, lb + ra});
int c = lb + rb;
return {a, b, c};
};
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func minCameraCover(root *TreeNode) int {
var dfs func(*TreeNode) (int, int, int)
dfs = func(root *TreeNode) (int, int, int) {
if root == nil {
return 1 << 29, 0, 0
}
la, lb, lc := dfs(root.Left)
ra, rb, rc := dfs(root.Right)
a := 1 + min(la, min(lb, lc)) + min(ra, min(rb, rc))
b := min(la+ra, min(la+rb, lb+ra))
c := lb + rb
return a, b, c
}
a, b, _ := dfs(root)
return min(a, b)
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function minCameraCover(root: TreeNode | null): number {
const dfs = (root: TreeNode | null): number[] => {
if (!root) {
return [1 << 29, 0, 0];
}
const [la, lb, lc] = dfs(root.left);
const [ra, rb, rc] = dfs(root.right);
const a = 1 + Math.min(la, lb, lc) + Math.min(ra, rb, rc);
const b = Math.min(la + ra, la + rb, lb + ra);
const c = lb + rb;
return [a, b, c];
};
const [a, b, _] = dfs(root);
return Math.min(a, b);
}