| comments | difficulty | edit_url | tags | |||||
|---|---|---|---|---|---|---|---|---|
true |
Medium |
|
You need to construct a binary tree from a string consisting of parenthesis and integers.
The whole input represents a binary tree. It contains an integer followed by zero, one or two pairs of parenthesis. The integer represents the root's value and a pair of parenthesis contains a child binary tree with the same structure.
You always start to construct the left child node of the parent first if it exists.
Example 1:
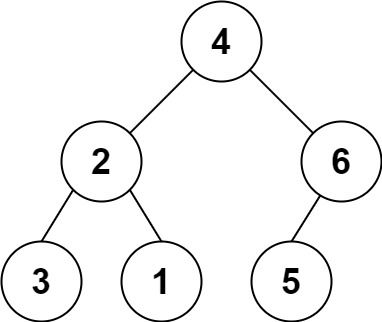
Input: s = "4(2(3)(1))(6(5))" Output: [4,2,6,3,1,5]
Example 2:
Input: s = "4(2(3)(1))(6(5)(7))" Output: [4,2,6,3,1,5,7]
Example 3:
Input: s = "-4(2(3)(1))(6(5)(7))" Output: [-4,2,6,3,1,5,7]
Constraints:
0 <= s.length <= 3 * 104sconsists of digits,'(',')', and'-'only.- All numbers in the tree have value at most than
230.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def str2tree(self, s: str) -> TreeNode:
def dfs(s):
if not s:
return None
p = s.find('(')
if p == -1:
return TreeNode(int(s))
root = TreeNode(int(s[:p]))
start = p
cnt = 0
for i in range(p, len(s)):
if s[i] == '(':
cnt += 1
elif s[i] == ')':
cnt -= 1
if cnt == 0:
if start == p:
root.left = dfs(s[start + 1 : i])
start = i + 1
else:
root.right = dfs(s[start + 1 : i])
return root
return dfs(s)/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode str2tree(String s) {
return dfs(s);
}
private TreeNode dfs(String s) {
if ("".equals(s)) {
return null;
}
int p = s.indexOf("(");
if (p == -1) {
return new TreeNode(Integer.parseInt(s));
}
TreeNode root = new TreeNode(Integer.parseInt(s.substring(0, p)));
int start = p;
int cnt = 0;
for (int i = p; i < s.length(); ++i) {
if (s.charAt(i) == '(') {
++cnt;
} else if (s.charAt(i) == ')') {
--cnt;
}
if (cnt == 0) {
if (start == p) {
root.left = dfs(s.substring(start + 1, i));
start = i + 1;
} else {
root.right = dfs(s.substring(start + 1, i));
}
}
}
return root;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* str2tree(string s) {
return dfs(s);
}
TreeNode* dfs(string s) {
if (s == "") return nullptr;
int p = s.find("(");
if (p == s.npos) return new TreeNode(stoi(s));
TreeNode* root = new TreeNode(stoi(s.substr(0, p)));
int start = p;
int cnt = 0;
for (int i = p; i < s.size(); ++i) {
if (s[i] == '(')
++cnt;
else if (s[i] == ')')
--cnt;
if (cnt == 0) {
if (start == p) {
root->left = dfs(s.substr(start + 1, i - start - 1));
start = i + 1;
} else
root->right = dfs(s.substr(start + 1, i - start - 1));
}
}
return root;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func str2tree(s string) *TreeNode {
var dfs func(s string) *TreeNode
dfs = func(s string) *TreeNode {
if s == "" {
return nil
}
p := strings.IndexAny(s, "(")
if p == -1 {
v, _ := strconv.Atoi(s)
return &TreeNode{Val: v}
}
v, _ := strconv.Atoi(s[:p])
root := &TreeNode{Val: v}
start := p
cnt := 0
for i := p; i < len(s); i++ {
if s[i] == '(' {
cnt++
} else if s[i] == ')' {
cnt--
}
if cnt == 0 {
if p == start {
root.Left = dfs(s[start+1 : i])
start = i + 1
} else {
root.Right = dfs(s[start+1 : i])
}
}
}
return root
}
return dfs(s)
}