Skip to content

Latest commit

 

History

History
304 lines (263 loc) · 8.66 KB

README.md

File metadata and controls

304 lines (263 loc) · 8.66 KB
comments difficulty edit_url tags
true
中等
树
数组
哈希表
分治
二叉树

106. 从中序与后序遍历序列构造二叉树

English Version

题目描述

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

 

示例 1:

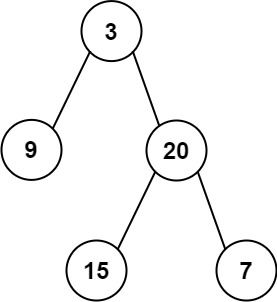
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

 

提示:

  • 1 <= inorder.length <= 3000
  • postorder.length == inorder.length
  • -3000 <= inorder[i], postorder[i] <= 3000
  • inorder 和 postorder 都由 不同 的值组成
  • postorder 中每一个值都在 inorder 中
  • inorder 保证是树的中序遍历
  • postorder 保证是树的后序遍历

解法

方法一：哈希表 + 递归

后序遍历的最后一个节点是根节点，我们可以根据这个特点找到根节点在中序遍历中的位置，然后递归地构造左右子树。

具体地，我们先用一个哈希表 $d$ 存储中序遍历中每个节点的位置。然后我们设计一个递归函数 $dfs(i, j, n)$，其中 $i$ 和 $j$ 分别表示中序遍历和后序遍历的起点，而 $n$ 表示子树包含的节点数。函数的逻辑如下：

  • 如果 $n \leq 0$，说明子树为空，返回空节点。
  • 否则，取出后序遍历的最后一个节点 $v$，然后我们在哈希表 $d$ 中找到 $v$ 在中序遍历中的位置，设为 $k$。那么左子树包含的节点数为 $k - i$，右子树包含的节点数为 $n - k + i - 1$。
  • 递归构造左子树 $dfs(i, j, k - i)$ 和右子树 $dfs(k + 1, j + k - i, n - k + i - 1)$，并连接到根节点上，最后返回根节点。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点个数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        def dfs(i: int, j: int, n: int) -> Optional[TreeNode]:
            if n <= 0:
                return None
            v = postorder[j + n - 1]
            k = d[v]
            l = dfs(i, j, k - i)
            r = dfs(k + 1, j + k - i, n - k + i - 1)
            return TreeNode(v, l, r)

        d = {v: i for i, v in enumerate(inorder)}
        return dfs(0, 0, len(inorder))

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private Map<Integer, Integer> d = new HashMap<>();
    private int[] postorder;

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        this.postorder = postorder;
        int n = inorder.length;
        for (int i = 0; i < n; ++i) {
            d.put(inorder[i], i);
        }
        return dfs(0, 0, n);
    }

    private TreeNode dfs(int i, int j, int n) {
        if (n <= 0) {
            return null;
        }
        int v = postorder[j + n - 1];
        int k = d.get(v);
        TreeNode l = dfs(i, j, k - i);
        TreeNode r = dfs(k + 1, j + k - i, n - k + i - 1);
        return new TreeNode(v, l, r);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        unordered_map<int, int> d;
        int n = inorder.size();
        for (int i = 0; i < n; ++i) {
            d[inorder[i]] = i;
        }
        function<TreeNode*(int, int, int)> dfs = [&](int i, int j, int n) -> TreeNode* {
            if (n <= 0) {
                return nullptr;
            }
            int v = postorder[j + n - 1];
            int k = d[v];
            auto l = dfs(i, j, k - i);
            auto r = dfs(k + 1, j + k - i, n - k + i - 1);
            return new TreeNode(v, l, r);
        };
        return dfs(0, 0, n);
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(inorder []int, postorder []int) *TreeNode {
	d := map[int]int{}
	for i, v := range inorder {
		d[v] = i
	}
	var dfs func(i, j, n int) *TreeNode
	dfs = func(i, j, n int) *TreeNode {
		if n <= 0 {
			return nil
		}
		v := postorder[j+n-1]
		k := d[v]
		l := dfs(i, j, k-i)
		r := dfs(k+1, j+k-i, n-k+i-1)
		return &TreeNode{v, l, r}
	}
	return dfs(0, 0, len(inorder))
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function buildTree(inorder: number[], postorder: number[]): TreeNode | null {
    const n = inorder.length;
    const d: Record<number, number> = {};
    for (let i = 0; i < n; i++) {
        d[inorder[i]] = i;
    }
    const dfs = (i: number, j: number, n: number): TreeNode | null => {
        if (n <= 0) {
            return null;
        }
        const v = postorder[j + n - 1];
        const k = d[v];
        const l = dfs(i, j, k - i);
        const r = dfs(k + 1, j + k - i, n - 1 - (k - i));
        return new TreeNode(v, l, r);
    };
    return dfs(0, 0, n);
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::collections::HashMap;
use std::rc::Rc;
impl Solution {
    pub fn build_tree(inorder: Vec<i32>, postorder: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
        let n = inorder.len();
        let mut d: HashMap<i32, usize> = HashMap::new();
        for i in 0..n {
            d.insert(inorder[i], i);
        }
        fn dfs(
            postorder: &[i32],
            d: &HashMap<i32, usize>,
            i: usize,
            j: usize,
            n: usize,
        ) -> Option<Rc<RefCell<TreeNode>>> {
            if n <= 0 {
                return None;
            }
            let val = postorder[j + n - 1];
            let k = *d.get(&val).unwrap();
            let left = dfs(postorder, d, i, j, k - i);
            let right = dfs(postorder, d, k + 1, j + k - i, n - 1 - (k - i));
            Some(Rc::new(RefCell::new(TreeNode { val, left, right })))
        }
        dfs(&postorder, &d, 0, 0, n)
    }
}