diff --git a/Courses/Differentiable Programming/010 Introduction.jl b/Courses/Differentiable Programming/010 Introduction.jl
new file mode 100644
index 0000000..3e6f848
--- /dev/null
+++ b/Courses/Differentiable Programming/010 Introduction.jl
@@ -0,0 +1,43 @@
+# # Course on Automatic Differentiation in Juia
+
+# ## Why derivatives ?
+
+# Derivatives are very useful in scietific computing.
+# A common use case is in iterative routines which
+# include finding roots and extreme points to nonlinear equations.
+# Ther are ways to do nonlinear optimization and nonlinear equation solving
+# without using derivatives but they are typically slow and non robust.
+# By including "higher order information" or the derivative, the iterative routine
+# gets more information and this opens up a whole new class of algorithms
+# that can be orders of magnitude faster than the ones that do not use the derivative.
+#
+# Manually deriving the derivative of a function (or algorithm) can be
+# tedious and error prone. A small error in the implementation of the derivative
+# can lead to that the optimal order of convergence in an iterative method is lost.
+# Indeed, the author of thise couse has lost many days from trying to locate that
+# last bug in a derivative implementation.
+#
+# Thinking about the rules for derivatives, they are quite simpl (here using an apostrophe
+# to denote the derivative):
+#
+# * Addition rule: $(f(x) + g(x))' = f'(x) + g'(x)$
+# * Product rule: $(f(x)g(x))' = f(x)g'(x) + f'(x)g(x)$
+# * Chain rule: $(f(g(x)))' = f'(g(x))g'(x)$
+#
+# It is natural to ask the question, should it not be possible to
+# automate the computation of these derivatives
+# and just have our program give back the derivative for us automatically.
+# In most cases, the answer to this is yes, it is possible to get the exact derivative
+# without having to implement any derivatives.
+# This is known as Automatic Differentiation typically shortened as AD.
+#
+#
+# ## Course goals
+#
+# In this course we will use the programming language Julia to look at AD.
+# The course goals is that after successfully finishing the course, you
+# should be able to:
+# * Use some of the popular AD tools in Julia, both for forward mode and reverse mode AD.
+# * Call optimization routines using derivatives computed with AD.
+# * Understand the theoretical background behind dual numbers and how they can be used for forward mode AD.
+# * Implement you own toy-version of forward mode AD.
diff --git a/Courses/Differentiable Programming/020 Descent.jl b/Courses/Differentiable Programming/020 Descent.jl
new file mode 100644
index 0000000..be40411
--- /dev/null
+++ b/Courses/Differentiable Programming/020 Descent.jl
@@ -0,0 +1,315 @@
+#nb import Pkg; Pkg.add(Pkg.PackageSpec(url="https://github.com/JuliaComputing/JuliaAcademyData.jl"))
+#nb using JuliaAcademyData; activate("Differentiable Programming")
+datapath(p) = joinpath("../../../JuliaAcademyData.jl/courses/Differentiable Programming", p) #src
+
+# # Descending to the top
+#
+# One killer app for derivatives is gradient descent. This is the process of
+# incrementally improving some algorithm by adjusting its "knobs" (the tuneable
+# parameters) based on its performance for some existing data.
+#
+# Each step incrementally improves on the previous set of parameters by
+# determining which way to "nudge" each parameter in order to improve on its output.
+# The trick is finding this direction efficiently.
+#
+# We could of course try changing each parameter individually and see which direction to move, but that's pretty tedious,
+# numerically fraught, and expensive. If, however, we knew the _partial derivatives_ with
+# respect to each parameter then we could simply "descend" down the slope of our error
+# function until we reach the bottom — that is, the minimum error!
+#
+# We all know how to draw a line on a graph — it just requires knowing the slope
+# and intercept of the equation
+#
+# $$
+# y = m x + b
+# $$
+#
+# What we want to do, though, is the inverse problem. We have a dataset and we
+# want to find a line that best fits it. We can use gradient descent to do this:
+#
+#  +#
+# This is trivial — and there are better ways to do this in the first place —
+# but the beauty of gradient descent is that it extends to much more complicated
+# examples. For example, we can even fit a differential equation with this method:
+#
+#
+#
+# This is trivial — and there are better ways to do this in the first place —
+# but the beauty of gradient descent is that it extends to much more complicated
+# examples. For example, we can even fit a differential equation with this method:
+#
+#  +#
+# But let's examine that line-fitting first as its simplicity makes a number of
+# points clear. To begin, let's load some data.
+
+using DifferentialEquations, CSV #src
+import Random #src
+Random.seed!(20) #src
+generate_data(ts) = solve(ODEProblem([1.0,1.0],(0.0,10.0),[1.5,1.0,3.0,1.0]) do du,u,p,t; du[1] = p[1]*u[1] - p[2]*prod(u); du[2] = -p[3]*u[2] + p[4]*prod(u); end, saveat=ts)[1,:].*(1.0.+0.02.*randn.()).+0.05.*randn.() #src
+ts = 0:.005:1 #src
+ys = generate_data(ts) #src
+CSV.write(datapath("data/020-descent-data.csv"), (t=ts, y=ys)) #src
+
+using CSV
+df = CSV.read(datapath("data/020-descent-data.csv"))
+#-
+using Plots
+scatter(df.t, df.y, xlabel="time", label="data")
+
+# Now we want to fit some model to this data — for a linear model we just need
+# two parameters:
+#
+# $$
+# y = m x + b
+# $$
+#
+# Lets create a structure that represents this:
+
+mutable struct LinearModel
+ m::Float64
+ b::Float64
+end
+(model::LinearModel)(x) = model.m*x + model.b
+
+# And create a randomly picked model to see how we do:
+linear = LinearModel(randn(), randn())
+plot!(df.t, linear.(df.t), label="model")
+
+# Of course, we just chose our `m` and `b` at random here, of course it's not
+# going to fit our data well! Let's quantify how far we are from an ideal line
+# with a _loss_ function:
+
+loss(f, xs, ys) = sum((f.(xs) .- ys).^2)
+loss(linear, df.t, df.y)
+
+# That's a pretty big number — and we want to decrease it. Let's update our plot
+# to include this loss value in the legend so we can keep track:
+
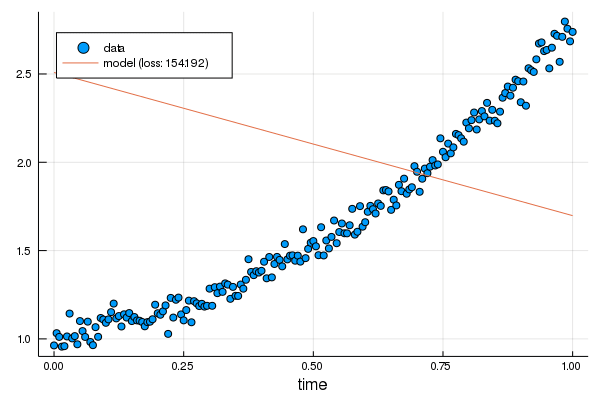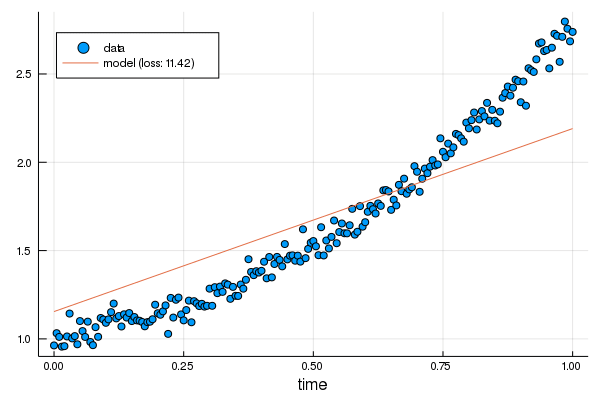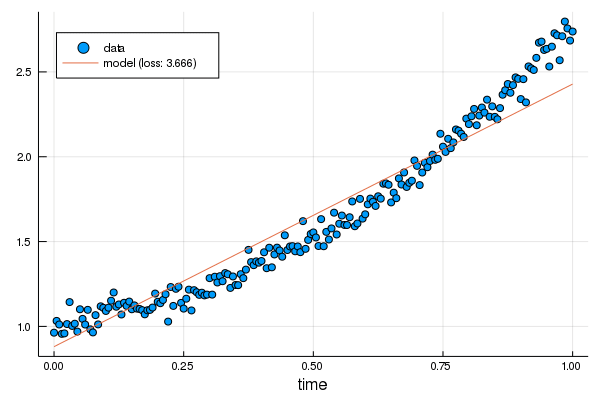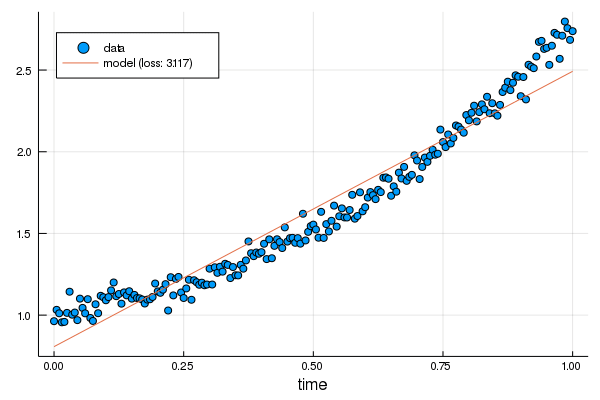
+p = scatter(df.t, df.y, xlabel="time", label="data")
+plot!(p, df.t, linear.(df.t), label="model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# And now we want to try to improve the fit. To do so, we just need to make
+# the loss function as small as possible. We can of course simply try a bunch
+# of values and brute-force a "good" solution. Plotting this as a three-dimensional
+# surface gives us the imagery of a hill, and our goal is to find our way to the bottom:
+
+ms, bs = (-1:.01:6, -2:.05:2.5)
+surface(ms, bs, [loss(LinearModel(m, b), df.t, df.y) for b in bs for m in ms], xlabel="m values", ylabel="b values", title="loss value")
+
+# A countour plot makes it a bit more obvious where the minimum is:
+
+contour(ms, bs, [loss(LinearModel(m, b), df.t, df.y) for b in bs for m in ms], levels=150, xlabel="m values", ylabel="b values")
+
+# But building those graphs are expensive! And it becomes completely intractible as soon as we
+# have more than a few parameters to fit. We can instead just try nudging the
+# current model's values to simply figure out which direction is "downhill":
+
+linear.m += 0.1
+plot!(p, df.t, linear.(df.t), label="new model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# We'll either have made things better or worse — but either way it's easy to
+# see which way to change `m` in order to improve our model.
+#
+# Essentially, what we're doing here is we're finding the derivative of our
+# loss function with respect to `m`, but again, there's a bit to be desired
+# here. Instead of evaluating the loss function twice and observing the difference,
+# we can just ask Julia for the derivative! This is the heart of differentiable
+# programming — the ability to ask a _complete program_ for its derivative.
+#
+# There are several techniques that you can use to compute the derivative. We'll
+# use the [Zygote package](https://fluxml.ai/Zygote.jl/latest/) first. It will
+# take a second as it compiles the "adjoint" code to compute the derivatives.
+# Since we're doing this in multiple dimensions, the two derivatives together
+# are called the gradient:
+
+using Zygote
+grads = Zygote.gradient(linear) do m
+ return loss(m, df.t, df.y)
+end
+grads
+
+# So there we go! Zygote saw that the model was gave it — `linear` — had two fields and thus
+# it computed the derivative of the loss function with respect to those two
+# parameters.
+#
+# Now we know the slope of our loss function — and thus
+# we know which way to move each parameter to improve it! We just need to iteratively walk
+# downhill! We don't want to take too large a step, so we'll multiply each
+# derivative by a "learning rate," typically called `η`.
+η = 0.001
+linear.m -= η*grads[1][].m
+linear.b -= η*grads[1][].b
+
+plot!(p, df.t, linear.(df.t), label="updated model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# Now we just need to do this a bunch of times!
+
+for i in 1:200
+ grads = Zygote.gradient(linear) do m
+ return loss(m, df.t, df.y)
+ end
+ linear.m -= η*grads[1][].m
+ linear.b -= η*grads[1][].b
+ i > 40 && i % 10 != 1 && continue
+#nb IJulia.clear_output(true)
+ scatter(df.t, df.y, label="data", xlabel="time", legend=:topleft)
+ display(plot!(df.t, linear.(df.t), label="model (loss: $(round(loss(linear, df.t, df.y), digits=3)))"))
+end
+
+#src === CREATING GIF ===
+f = let #src
+ linear = LinearModel(randn(), randn()) #src
+ f = @gif for i in 1:150 #src
+ grads = Zygote.gradient(linear) do m #src
+ return loss(m, df.t, df.y) #src
+ end #src
+ linear.m -= η*grads[1][].m #src
+ linear.b -= η*grads[1][].b #src
+ scatter(df.t, df.y, label="data", xlabel="time", legend=:topleft) #src
+ plot!(df.t, linear.(df.t), label="model (loss: $(round(loss(linear, df.t, df.y), digits=3)))") #src
+ end #src
+ mv(f.filename, datapath("images/020-linear.gif")) #src
+end #src
+
+
+
+# That's looking pretty good now! You might be saying this is crazy — I know
+# how to do a least squares fit! And you'd be right — in this case you can
+# easily do this with a linear solve of the system of equations:
+m, b = [df.t ones(size(df.t))] \ df.y
+
+@show (m, b)
+@show (linear.m, linear.b);
+
+# ## Exercise: Use gradient descent to fit a quadratic model to the data
+#
+# Obviously a linear fit leaves a bit to be desired here. Try to use the same
+# framework to fit a quadratic model. Check your answer against the algebraic
+# solution with the `\` operator.
+
+struct PolyModel
+ p::Vector{Float64}
+end
+function (m::PolyModel)(x)
+ r = m.p[1]*x^0
+ for i in 2:length(m.p)
+ r += m.p[i]*x^(i-1)
+ end
+ return r
+end
+poly = PolyModel(rand(3))
+loss(poly, df.t, df.y)
+η = 0.001
+for i in 1:1000
+ grads = Zygote.gradient(poly) do m
+ return loss(m, df.t, df.y)
+ end
+ poly.p .-= η.*grads[1].p
+end
+scatter(df.t, df.y, label="data", legend=:topleft)
+plot!(df.t, poly.(df.t), label="model by descent")
+plot!(df.t, PolyModel([df.t.^0 df.t df.t.^2] \ df.y).(df.t), label="model by linear solve")
+
+# ## Nonlinearities
+#
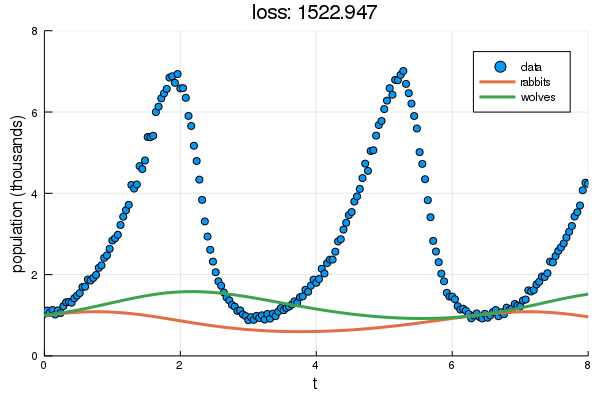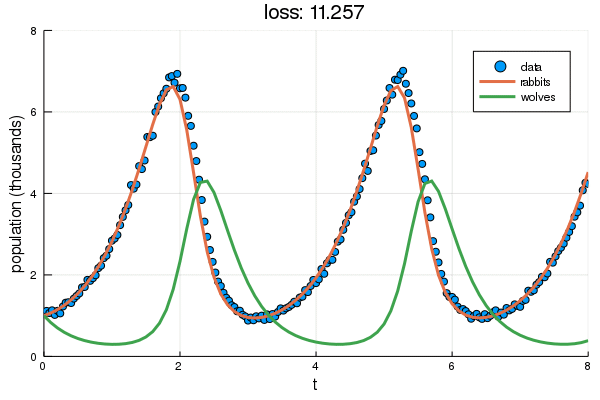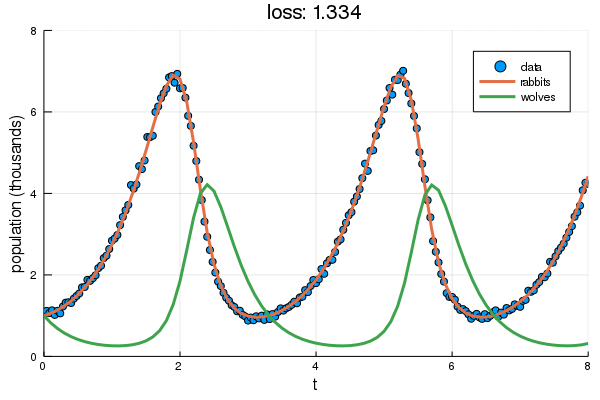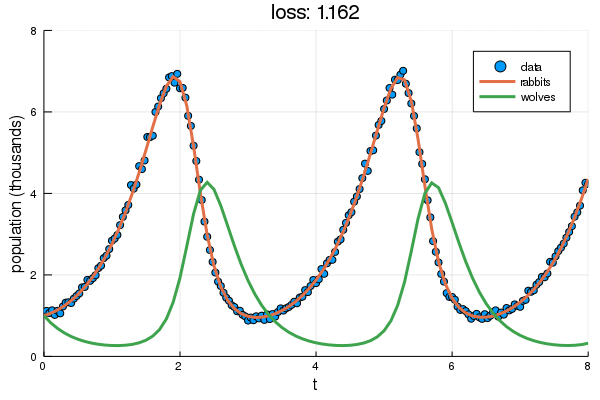
+# Let's see what happens when load a bit more data:
+
+let #src
+ ts = 0:.04:8 #src
+ ys = generate_data(ts) #src
+ CSV.write(datapath("data/020-descent-data-2.csv"), (t=ts, y=ys)) #src
+end #src
+df2 = CSV.read(datapath("data/020-descent-data-2.csv"))
+scatter(df2.t, df2.y, xlabel="t", label="more data")
+
+# Now what? This clearly won't be fit well with a low-order polynomial, and
+# even a high-order polynomial will get things wrong once we try to see what
+# will happen in the "future"!
+#
+# Let's use a bit of knowledge about where this data comes from: these happen
+# to be the number of rabbits in a predator-prey system! We can express the
+# general behavior with a pair of differential equations:
+#
+# $$
+# x' = \alpha x - \beta x y \\
+# y' = -\delta y + \gamma x y
+# $$
+#
+# * $x$ is the number of rabbits (🐰)
+# * $y$ is the number of wolves (🐺)
+# * $\alpha$ and $\beta$ describe the growth and death rates for the rabbits
+# * $\gamma$ and $\delta$ describe the growth and death rates for the wolves
+#
+# But we don't know what those rate constants are — all we have is the population
+# of rabbits over time.
+#
+# These are the classic Lotka-Volterra equations, and can be expressed in Julia
+# using the [DifferentialEquations](https://github.com/JuliaDiffEq/DifferentialEquations.jl) package:
+using DifferentialEquations
+function rabbit_wolf(du,u,p,t)
+ 🐰, 🐺 = u
+ α, β, δ, γ = p
+ du[1] = α*🐰 - β*🐰*🐺
+ du[2] = -δ*🐺 + γ*🐰*🐺
+end
+u0 = [1.0,1.0]
+tspan = extrema(df2.t)
+p = rand(4).+1 # We don't know what this is!
+## But lets see what the model looks like right now:
+prob = ODEProblem(rabbit_wolf,u0,tspan,p)
+sol = solve(prob, Tsit5(), saveat=df2.t)
+
+scatter(df2.t, df2.y, xlabel="t", label="more data")
+plot!(sol, label=["rabbits","wolves"])
+
+# So we're going to have to improve this — unlike the previous examples, we don't
+# have an easy algebraic solution here! But let's try using gradient descent.
+# The easiest way to get gradients out of a differential equation solver right
+# now is through the [DiffEqFlux package](https://github.com/JuliaDiffEq/DiffEqFlux.jl), and instead of manually converging,
+# we can use the Flux package to automatically (and more smartly) handle the gradient descent. Just
+# like before, though, we compute the loss of the model evaluation — and in this
+# case the model is _solving a differential equation!_
+using Flux, DiffEqFlux
+p = Flux.param(ones(4))
+diffeq_loss(p, xs, ys) = sum(abs2, diffeq_rd(p,prob,Tsit5(),saveat=df2.t)[1,:] .- df2.y)
+
+# This works slightly differently — we now track the gradients directly in the
+# p vector:
+p.grad
+#-
+l = diffeq_loss(p, df2.t, df2.y)
+#-
+DiffEqFlux.Tracker.back!(l) # we need to back-propagate our tracking of the gradients
+p.grad # but now we can see the gradients involved in that computation!
+
+# So now we can do exactly the same thing as before: iteratively update the parameters
+# to descend to a (hopefully) well-fit model:
+#
+# ```julia
+# p.data .-= η*p.grad
+# ```
+#
+# But we can be a bit smarter about this just by asking Flux to handle everything
+# with its train! function and associated functionality:
+
+data = Iterators.repeated((df2.t, df2.y), 150)
+opt = ADAM(0.1)
+history = Any[] #src
+cb = function () #callback function to observe training
+#nb IJulia.clear_output(true)
+ plt = scatter(df2.t, df2.y, label="data", ylabel="population (thousands)", xlabel="t")
+ display(plot!(plt, solve(remake(prob,p=Flux.data(p)),Tsit5(),saveat=0.1),
+ ylim=(0,8), label=["rabbits","wolves"], title="loss: $(round(Flux.data(diffeq_loss(p, df2.t, df2.y)), digits=3))"))
+ push!(history, plt) #src
+end
+Flux.train!((xs, ys)->diffeq_loss(p, xs, ys), [p], data, opt, cb = cb)
+
+f = @gif for i in 1:length(history) #src
+ plot(history[i]) #src
+end #src
+mv(f.filename, datapath("images/020-diffeq.gif")) #src
+
+# # Summary
+#
+# You can now see the power of differentiating whole programs — we can easily
+# and efficiently tune parameters without brute forcing solutions. Gradient
+# descent easily extends to machine learning and artificial intelligence
+# applications — and there are a number of tricks that can increase its efficiency
+# and help avoid local minima. There are a variety of other places where knowing the gradient can
+# be powerful and helpful.
diff --git a/Courses/Differentiable Programming/030 Neural Differential Equations.jl b/Courses/Differentiable Programming/030 Neural Differential Equations.jl
new file mode 100644
index 0000000..0b0f013
--- /dev/null
+++ b/Courses/Differentiable Programming/030 Neural Differential Equations.jl
@@ -0,0 +1,86 @@
+using Flux, DiffEqFlux, StochasticDiffEq, Plots, DiffEqMonteCarlo
+
+u0 = Float32[2.; 0.]
+datasize = 30
+tspan = (0.0f0,1.0f0)
+
+function trueODEfunc(du,u,p,t)
+ true_A = [-0.1 2.0; -2.0 -0.1]
+ du .= ((u.^3)'true_A)'
+end
+t = range(tspan[1],tspan[2],length=datasize)
+mp = Float32[0.2,0.2]
+function true_noise_func(du,u,p,t)
+ du .= mp.*u
+end
+prob = SDEProblem(trueODEfunc,true_noise_func,u0,tspan)
+
+# Take a typical sample from the mean
+monte_prob = MonteCarloProblem(prob)
+monte_sol = solve(monte_prob,SOSRI(),num_monte = 100)
+monte_sum = MonteCarloSummary(monte_sol)
+sde_data = Array(timeseries_point_mean(monte_sol,t))
+
+dudt = Chain(x -> x.^3,
+ Dense(2,50,tanh),
+ Dense(50,2))
+ps = Flux.params(dudt)
+n_sde = x->neural_dmsde(dudt,x,mp,tspan,SOSRI(),saveat=t,reltol=1e-1,abstol=1e-1)
+
+pred = n_sde(u0) # Get the prediction using the correct initial condition
+
+dudt_(u,p,t) = Flux.data(dudt(u))
+g(u,p,t) = mp.*u
+nprob = SDEProblem(dudt_,g,u0,(0.0f0,1.2f0),nothing)
+
+monte_nprob = MonteCarloProblem(nprob)
+monte_nsol = solve(monte_nprob,SOSRI(),num_monte = 100)
+monte_nsum = MonteCarloSummary(monte_nsol)
+#plot(monte_nsol,color=1,alpha=0.3)
+p1 = plot(monte_nsum, title = "Neural SDE: Before Training")
+scatter!(p1,t,sde_data',lw=3)
+
+scatter(t,sde_data[1,:],label="data")
+scatter!(t,Flux.data(pred[1,:]),label="prediction")
+
+function predict_n_sde()
+ n_sde(u0)
+end
+loss_n_sde1() = sum(abs2,sde_data .- predict_n_sde())
+loss_n_sde10() = sum([sum(abs2,sde_data .- predict_n_sde()) for i in 1:10])
+Flux.back!(loss_n_sde1())
+
+data = Iterators.repeated((), 10)
+opt = ADAM(0.025)
+cb = function () #callback function to observe training
+ sample = predict_n_sde()
+ # loss against current data
+ display(sum(abs2,sde_data .- sample))
+ # plot current prediction against data
+ cur_pred = Flux.data(sample)
+ pl = scatter(t,sde_data[1,:],label="data")
+ scatter!(pl,t,cur_pred[1,:],label="prediction")
+ display(plot(pl))
+end
+
+# Display the SDE with the initial parameter values.
+cb()
+
+Flux.train!(loss_n_sde1 , ps, Iterators.repeated((), 100), opt, cb = cb)
+Flux.train!(loss_n_sde10, ps, Iterators.repeated((), 20), opt, cb = cb)
+
+dudt_(u,p,t) = Flux.data(dudt(u))
+g(u,p,t) = mp.*u
+nprob = SDEProblem(dudt_,g,u0,(0.0f0,1.2f0),nothing)
+
+monte_nprob = MonteCarloProblem(nprob)
+monte_nsol = solve(monte_nprob,SOSRI(),num_monte = 100)
+monte_nsum = MonteCarloSummary(monte_nsol)
+#plot(monte_nsol,color=1,alpha=0.3)
+p2 = plot(monte_nsum, title = "Neural SDE: After Training", xlabel="Time")
+scatter!(p2,t,sde_data',lw=3,label=["x" "y" "z" "y"])
+
+plot(p1,p2,layout=(2,1))
+
+savefig("neural_sde.pdf")
+savefig("neural_sde.png")
diff --git a/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl b/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl
new file mode 100644
index 0000000..6cc7a7f
--- /dev/null
+++ b/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl
@@ -0,0 +1,260 @@
+# # How To Aim Your Flagon
+
+#-
+
+# ## Loading your Trebuchet
+
+#-
+
+# Today we practice the ancient medieval art of throwing stuff. First up, we load our trebuchet simulator, Trebuchet.jl.
+
+using Trebuchet
+
+# We can see what the trebuchet looks like, by explicitly creating a trebuchet state, running a simulation, and visualising the trajectory.
+
+t = TrebuchetState()
+simulate(t)
+visualise(t)
+
+# For training and optimisation, we don't need the whole visualisation, just a simple function that accepts and produces numbers. The `shoot` function just takes a wind speed, angle of release and counterweight mass, and tells us how far the projectile got.
+
+function shoot((wind, angle, weight))
+ Trebuchet.shoot((wind, Trebuchet.deg2rad(angle), weight))[2]
+end
+
+#-
+
+shoot([0, 45, 400])
+
+# It's worth playing with these parameters to see the impact they have. How far can you throw the projectile, tweaking only the angle of release?
+
+shoot([0, 40, 400])
+
+#-
+
+# There's actually a much better way of aiming the trebuchet. Let's load up a machine learning library, Flux, and see what we can do.
+
+using Flux, Trebuchet
+using Flux.Tracker: gradient, forwarddiff
+
+# Firstly, we're going to wrap `shoot` to take a _parameter vector_ (just a list of the three numbers we're interested in). There's also a call to `forwarddiff` here, which tells Flux to differentiate the trebuchet itself using forward mode. The number of parameters is small, so forward mode will be the most efficient way to do it. Otherwise Flux defaults to reverse mode.
+
+shoot(ps) = forwarddiff(p->shoot(p...), ps)
+
+# We can get a distance as usual.
+
+shoot([0, 45, 200])
+
+# But we can also get something much more interesting: *gradients* for each of those parameters with respect to distance.
+
+gradient(x->forwarddiff(shoot, x), [0.0, 45, 200])
+
+# What does these numbers mean? The gradient tells us, very roughly, that if we increase a parameter – let's say we make wind speed 1 m/s stronger – distance will also increase by about 4 metres. Let's try that.
+Zygote.gradient(x->forwarddiff(shoot, x), [0.0, 45, 200])
+
+shoot([1, 45, 200])
+
+# Lo and behold, this is indeed about four metres further!
+
+shoot([1, 45, 200]) - shoot([0, 45, 200])
+
+# So this seems like very useful information if we're trying to aim, or maximise distance. Notice that our gradient for the release angle is negative – increasing angle will decrease distance, so in other words we should probably *decrease* angle if we want more distance. Let's try that.
+
+shoot([0, 10, 200])
+
+# Oh no, this is actually *less* far than before!
+
+#-
+
+# So if the angle is too shallow, the projectile doesn't spend enough time in the air to gain any distance before hitting the ground. But if it's too high, the projectile doesn't have enough horizontal speed even with lots of time in the air. So we'll have to find a middle ground.
+#
+# More generally, the lesson here is that the gradient only gives you limited information; it helps us take a small step towards a better aim, and we can keep iterating to get to the best possible aim. For example, we choose a starting angle:
+
+angle = 45
+shoot([0, angle, 200])
+
+# Get a gradient for `angle` alone:
+
+dangle = gradient(angle -> shoot(Tracker.collect([0, angle, 200])), angle)[1] |> Flux.data
+
+# Update the angle, using the learning rate η:
+
+η = 10
+angle += η*dangle
+
+#-
+
+shoot([0, angle, 200])
+
+# Now we just lather, rinse and repeat! Ok, maybe we should write a loop to automate this a bit.
+
+for i = 1:10
+ dangle = gradient(angle -> shoot(Tracker.collect([0, angle, 200])), angle)[1] |> Flux.data
+ angle += η*dangle
+ @show angle
+end
+shoot([0, angle, 200])
+
+# Notice how the change in the angle slows down as things converge. Turns out the best angle is about 30 degrees, and we can hit about 90 metres.
+#
+# We can make this nicely repeatable and get the best angle for any given wind speed.
+
+function best_angle(wind)
+ angle = 45
+ objective(angle) = shoot(Tracker.collect([wind, angle, 200]))
+ for i = 1:10
+ dangle = gradient(objective, angle)[1] |> Flux.data
+ angle += η*dangle
+ end
+ return angle
+end
+
+#-
+
+best_angle(0)
+
+#-
+
+best_angle(10)
+
+#-
+
+best_angle(-10)
+
+# It turns out that if the wind is on our side, we should just throw the projectile upwards and let it get blown along. If the wind is strong against us, just chuck that stone right into it.
+
+t = TrebuchetState(release_angle = deg2rad(19), wind_speed = -10)
+simulate(t)
+visualise(t)
+
+# ## Accuracy Matters
+
+#-
+
+# In optimisation terms, we just created an objective (distance) and tried to maximise that objective. Flinging boulders as far as possible has its moments, but lacks a certain subtlety. What if we instead want to hit a precise target?
+
+t = TrebuchetState()
+simulate(t)
+visualise(t, 50)
+
+# The way to do this is to state the problem in terms of maximising, or minisming, some number – the objective. In this case, an easy way to come up with an objective is to take the difference from our target (gets closer to 0 as aim gets better) and square it (so it's always positive: 0 is the lowest *and* best possible score).
+
+#-
+
+# Here's a modified `best_angle` function that takes a target and tells us the distance it acheived.
+
+η = 0.1
+function best_angle(wind, target)
+ angle = 45
+ objective(angle) = (shoot(Tracker.collect([wind, angle, 200])) - target)^2
+ for i = 1:30
+ dangle = gradient(objective, angle)[1] |> Flux.data
+ angle -= η*dangle
+ end
+ return angle, shoot([wind, angle, 200])
+end
+
+# It's pretty accurate!
+
+best_angle(0, 50)
+
+# Even when we try to push it, by making wind really strong.
+
+best_angle(-20, 35)
+
+#-
+
+t = TrebuchetState(release_angle = deg2rad(21.8), weight = 200, wind_speed = -20)
+simulate(t)
+visualise(t, 35)
+
+# ## Siege Weapon Autopilot
+
+#-
+
+# Finally, we go one level more meta by training a neural network to aim the trebuchet for us. Rather than solving a whole optimisation problem every time we want to aim, we can just ask the network for good parameters and get them in constant time.
+#
+# Here's a simple multi layer perceptron. Its input is two parameters (wind speed and target) and its output is two more (release angle and counterweight mass).
+
+model = Chain(Dense(2, 16, σ),
+ Dense(16, 64, σ),
+ Dense(64, 16, σ),
+ Dense(16, 2)) |> f64
+
+θ = params(model)
+
+function aim(wind, target)
+ angle, weight = model([wind, target])
+ angle = σ(angle)*90
+ weight = weight + 200
+ angle, weight
+end
+
+distance(wind, target) = shoot(Tracker.collect([wind, aim(wind, target)...]))
+
+# The model's initial guesses will be fairly random, and miss the mark.
+
+aim(0, 70)
+
+#-
+
+distance(0, 70)
+
+# However, just as before, we can define an objective – or loss – and get gradients.
+
+function loss(wind, target)
+ try
+ (distance(wind, target) - target)^2
+ catch e
+ # Roots.jl sometimes give convergence errors, ignore them
+ param(0)
+ end
+end
+
+loss(0, 70)
+
+# This time, though, we'll get gradients for the *model parameters*, and updating these will improve the network's accuracy. This works because we're able to differentiate the *whole program*; the backwards pass propagates errors through the trebuchet simulator and then through the ML model.
+
+dθ = gradient(θ) do
+ loss(0, 70)
+end
+dθ[model[1].W]
+
+#-
+
+DIST = (20, 100) # Maximum target distance
+SPEED = 5 # Maximum wind speed
+
+lerp(x, lo, hi) = x*(hi-lo)+lo
+
+randtarget() = (randn() * SPEED, lerp(rand(), DIST...))
+
+#-
+
+using Statistics
+
+meanloss() = mean(sqrt(loss(randtarget()...)) for i = 1:100)
+
+opt = ADAM()
+
+dataset = (randtarget() for i = 1:10_000)
+
+Flux.train!(loss, θ, dataset, opt, cb = Flux.throttle(() -> @show(meanloss()), 10))
+
+# After only a few minutes of training, we're getting solid accuracy, even on hard wind speeds and targets. You can run the training loop again to improve the accuracy even further.
+
+wind, target = -10, 50
+angle, mass = Flux.data.(aim(wind, target))
+t = TrebuchetState(release_angle = deg2rad(angle), weight = mass, wind_speed = wind)
+simulate(t)
+visualise(t, target)
+
+# Notice that aiming with a neural net in one shot is significantly faster than solving the optimisation problem; and we only have a small loss in accuracy.
+
+@time aim(wind, target)
+
+#-
+
+@time best_angle(wind, target)
+
+#-
diff --git a/Courses/Differentiable Programming/050 Forward Differentiation.jl b/Courses/Differentiable Programming/050 Forward Differentiation.jl
new file mode 100644
index 0000000..fdc0453
--- /dev/null
+++ b/Courses/Differentiable Programming/050 Forward Differentiation.jl
@@ -0,0 +1,325 @@
+module ADPackages #src
+# Some settings for running this interactively #src
+interactive_use = false #src
+plotting_off = false #src
+using BenchmarkTools #src
+if interactive_use #src
+BenchmarkTools.DEFAULT_PARAMETERS.seconds = 0.1 #src
+end #src
+
+# # Using AD packages
+#
+# While a theoretical understanding behind how automatic differentiation work
+# is interesting, in practice, being able to use existing AD packages might
+# be good enough so this is where we will start.
+# Julia has many excellent packages for AD. The purpose of this lecture
+# for you to try a few of them out and apply them to real problems like solving
+# optimization problems using AD.
+
+# ## ForwardDiff
+#
+# The most popular package for AD in Julia is [`ForwardDiff`](https://github.com/JuliaDiff/ForwardDiff.jl).
+# It uses something called *forward mode automatic differentiation* using "Dual numbers"
+# and operator overloading. Forward mode AD is efficient if the function
+# being differentiated is $\mathbb{R}^N -> \mathbb{R}^M$ with $N <= M$. In other words,
+# the dimension of the input argument should be equal or greater than the number of
+# output arguments.
+# Foroward mode AD is however not so efficient for example when `M = 1` and `N` is big, which is common in
+# e.g. machine learning. In these cases *reverse mode automatic differentiation* is
+# more efficient, and we will look at that later.
+
+# ### Derivative of scalar functions
+#
+# To have a function to start experimenting with, we define the (scalar to
+# scalar) function `f(x)` and its analytical derivative
+# `fp(x)`
+
+f(x) = exp(x) / (sin(x)^3 + cos(x)^3);
+fp(x) = exp(x) * (3sin(x) + sin(3x) + 2cos(3x)) / 2(sin(x)^3 + cos(x)^3)^2;
+
+# We can visualize the function and the derivative (here using the Plots.jl package)
+if !plotting_off #src
+using Plots
+end #src
+xs = 0.0:0.01:1.4
+if !plotting_off #src
+plot(xs, [f.(xs), fp.(xs)]; labels = ["f" "fp"])
+end #src
+
+# The only thing to do to differentiate this function using AD is to import `ForwardDiff`
+# and call the `ForwardDiff.derivative` function with the function we want to differentiate and
+# at what point we want the derivative. The function should take a scalar as an argument
+# and return a scalar and that is what our function `f` above does.
+
+import ForwardDiff
+ad_derivative = ForwardDiff.derivative(f, pi/4)
+analytical_derivative = fp(pi/4)
+@assert ad_derivative ≈ analytical_derivative #src
+@show ad_derivative - analytical_derivative;
+
+# We can see that the AD derivative is "exact" (at least exact in the sense of floating
+# point precision) to the analytical ones.
+
+# #### Performance
+#
+# It can be interesting to see what the performance of using AD vs the the performance of the
+# analytical derivative. We can use the benchmark framework [`BenchmarkTools.jl`](https://github.com/JuliaCI/BenchmarkTools.jl)
+# to help us make accurate benchmarks even for functions that execute very quickly.
+
+using BenchmarkTools
+
+@assert VERSION < v"1.1" "revise benchmarking for 1.1" #src
+
+############################################################ #src
+# TODO: THIS IS ONLY TRUE ON MASTER, THE OPTIMIZATION DOES NOT HAPPEN ON JULIA 1.0.1 #src
+# If we do some napkin math, we can see that the reported time here is completely bogus! #src
+# Making the not too terrible assumption that a CPU can do one operation per clockcycle and that #src
+# the CPU you are using has approximately 3 GHz then one instruction should take ~0.3 ns which is #src
+# much longer than the reported time here. And computing this derivative need to compute `sin`, `cos` #src
+# etc which take many CPU instructions. #src
+# We have now encounted one of hard problems when benchmarking, to make sure that the computer is actually #src
+# computing the things you want it to. What happens here is that the Julia compiler is able #src
+# to figure out that the input we gave the function (`pi/4`) is a constant and the optimizer #src
+# then figures out the result during compile time. We can see this as follows: #src
+# #src
+#g() = ForwardDiff.derivative(f, pi/4) #src
+# #src
+## Looking at the generated code for #src
+# #src
+#@code_llvm g() #src
+# #src
+# We can see that the function has been optimized to just return a single value. #src
+# The exact value looks a bit odd because it is written #src
+# but reinterpreting it as a Float64 value we can see that it is just the same #src
+# derivative as was returned from ForwardDiff: #src
+# #src
+#@show reinterpret(Float64, 0x4008D06AE62ADC94) #src
+# #src
+#@show ForwardDiff.derivative(f, pi/4) #src
+# #src
+# One way we can trick the optimizer (at least with the current version of it) to not optimized #src
+# away the computation #src
+# is to encapsulate our value in a container like a [`Ref`](https://docs.julialang.org/en/v1/base/c/#Core.Ref) #src
+# #src
+##################################################################################### #src
+
+# A function can be benchmarked by prepending the call with `@btime`.
+# This will run the function multiple time and collect statistics on the
+# time it took to execute the function:
+
+println("Original function")
+@btime f(pi/4);
+println("AD derivative")
+@btime ForwardDiff.derivative(f, pi/4);
+println("Analytical derivative")
+@btime fp(pi/4);
+
+# We can here see that for the way we implemented the analytical derivative there is virtually no
+# performance difference between the AD version and the analyitical version.
+# However, it should be noted that the current version of the analytical function is not the
+# one with the best performance. Feel free to try to improve it.
+
+# A nice thing about AD is that you don't have to spend time making sure that
+# not only is the derivative correct, but that it is also efficiently computed.
+# By using AD, you get "free" performance for the derivative by optimizing the function itself.
+
+# #### Second derivatives
+#
+# For scalar functions `ForwardDiff` does not come with built in functionality for computing
+# the second derivative. It is, fortunately, very easy to create such a function ourselves.
+# The second derivative is just the derivative of the derivative which we can implement as:
+
+derivative2(f, x) = ForwardDiff.derivative(z -> ForwardDiff.derivative(f, z), x)
+
+@assert derivative2(f, pi/4) ≈ -6.203532787672101 #src
+@show derivative2(f, pi/4);
+
+# Here, we created an anonymous function that computes derivatives of `f`,
+# `z -> ForwardDiff.derivative(f, z)`, and then we used that as the input
+# derivative for another `ForwardDiff.derivative` call. The derivative
+# of the derivative gives the second derivative. Simple!
+# Feel free to compute the second derivative by hand and verify that the result
+# is correct (and appreciate that AD savees you from doing it in the first place).
+# The correct analytical result is `-2sqrt(2) * exp(pi/4)`.
+
+# #### Differentiating functions with parameters
+#
+# It is common to have a function that depends on some parameters that are considered
+# fixed in the context of differentiation.
+# An example of this might be the function `g` (and its derivative `gp) below:
+
+g(x, a) = (x - a)^3
+gp(x, a) = 3*(x - a)^2
+
+# Here, `g` has the parameter `a` and we want to take the derivative with respect to `x`.
+# Recall that `ForwardDiff.derivative` needs a function that takes only one
+# argument, but `g` above takes two arguments, so it clearly cannot be used directly.
+# The solution is to create what is typically called a "closure", which is a new function
+# that "closes" over some parameter space.
+# For example, consider:
+
+const a = 3
+g2(x) = g(x, a)
+
+@show (2 - a)^3
+@show g2(2);
+
+# We now have a new function `g2` which takes only one argument (`x`) and "closes" over the
+# variable `a`. We can now differentiate `g2`.
+
+@show ForwardDiff.derivative(g2, 2.0)
+@show gp(2.0, 3);
+
+# It is possible to write this a bit more succintly using an anonymous function
+
+ForwardDiff.derivative(x -> g(x, a), 2.0)
+
+# ## Gradients
+#
+# If our function takes a vector as input and returns a scalar, the derivative
+# is a vector (called a gradient) which gives the sensitivity of the output with respect to
+# all inputs. A quite common function to use in examples involving optimization
+# is the [Rosenbrock function](https://en.wikipedia.org/wiki/Rosenbrock_function), defined as:
+
+function rosenbrock(x)
+ a = one(eltype(x))
+ b = 100 * a
+ result = zero(eltype(x))
+ for i in 1:length(x)-1
+ result += (a - x[i])^2 + b*(x[i+1] - x[i]^2)^2
+ end
+ return result
+end
+
+# Evaluating `rosenbrock` with a vector input indeed gives a scalar back.
+
+rosenbrock([1.0, 0.5, 2.0])
+@assert rosenbrock([1.0, 0.5, 2.0]) == 331.5 #src
+
+# We can see how this function looks by plotting it
+
+xs = -3:0.1:3
+ys = -3:0.1:3
+zs = [rosenbrock([x, y]) for x in xs, y in ys]
+if !plotting_off #src
+contour(xs, ys, zs; levels=40)
+end #src
+
+# Evaluating the `gradient` is almost as simple as the `derivative`:
+
+x_vec = [1.0, 2.0]
+ForwardDiff.gradient(rosenbrock, x_vec)
+
+# ### Performance
+#
+# When evaluating the gradient we are dealing with `Vector`s which require allocation
+# so there are a few extra performance considerations for `gradient` compared to `derivative`
+
+# #### Preallocating output
+#
+# `ForwardDiff.gradient` returns a `Vector` which needs to be allocated. We can preallocate
+# this so `ForwardDiff` doesn't need to to it by itself.
+
+z_vec = similar(x_vec)
+ForwardDiff.gradient!(z_vec, rosenbrock, x_vec)
+@show z_vec;
+
+# The result was now stored in the, by us, allocated `z_vec`. We can check the performance difference
+
+println("No preallocation")
+@btime ForwardDiff.gradient(rosenbrock, $x_vec)
+println("No preallocation")
+@btime ForwardDiff.gradient!($z_vec,rosenbrock, $x_vec)
+
+# We can see that we do one allocation less and that performance is significantly
+# improved.
+
+# #### Preallocating internal datastructures
+#
+# Even though we preallocated the output vector there are some
+# internal data structures used by ForwardDiff that we in addition can preallocate
+# This is done by creating a `GradientConfig`:
+
+gradient_cache = ForwardDiff.GradientConfig(rosenbrock, x_vec)
+@btime ForwardDiff.gradient!($z_vec, rosenbrock, $x_vec, $gradient_cache);
+
+# Which as we can see further increase performance.
+# All of this is documented in the ForwardDiff manual so the takehome message is
+# to read the manual of the package one uses. There are often valuable information
+# there that could (like in this case) significantly improve performance.
+
+# ### Solving optimization using ForwardDiff
+#
+# [`Optim`](https://github.com/JuliaNLSolvers/Optim.jl) is a package that has many useful optimization routines.
+# If you can provide the gradient (and even sec) you get access to optimization routines that can
+# have significantly better performance. Lets use first try to just optimize the function without
+# using any gradient information. This will default to using the
+# [Nelder-Mead method](https://en.wikipedia.org/wiki/Nelder%E2%80%93Mead_method).
+# We also stick a `@btime` in there to see how long time the optimization routine take.
+using Random; Random.seed!(1234) #src
+using Optim
+x0 = zeros(10)
+@btime optimize(rosenbrock, x0)
+
+# We can see that we require approximately 620 evaluations of `rosenbrock` before
+# a minimum was found. Let's try giving `Optim` the gradient as well:
+#
+using Random; Random.seed!(1234) #src
+const gradient_cache_optim = ForwardDiff.GradientConfig(rosenbrock, x0)
+const rosenbrock_gradient! = (z, x) -> ForwardDiff.gradient!(z,rosenbrock, x, gradient_cache_optim)
+
+@btime optimize(rosenbrock, rosenbrock_gradient!, x0)
+
+# Now we only called the function 92 times (and in addition the gradient 153 times)
+# Looking at the time taken this was almost a 3x speedup. The minimum we found had a
+# was also significantly smaller than when we used Nelder-Mead
+
+# ## Hessians
+# It is also possible to compute Hessians (second derivative) in a very similar way to `gradient`
+
+ForwardDiff.hessian(rosenbrock, [1.0, 2.0])
+
+# We leave out the details for `ForwardDiff.hessian` here and instead refer to the [`ForwardDiff.hessian`](http://www.juliadiff.org/ForwardDiff.jl/stable/user/api.html#Hessians-of-f(x::AbstractArray)::Real-1)
+# documentation.
+
+# ## Jacobians
+#
+# If our function takes a vector as argument and returns a vector, the derivative is a `Matrix` which
+# is known as the Jacobian. This derivative is useful when we want to solve a nonlinear system of
+# equations.
+# Let's consider the following function that slightly resembles the `rosenbrock` function:
+
+function rosenbrock_vector(x)
+ return [
+ 1 - x[1],
+ 10(x[2]-x[1]^2)
+ ]
+end
+
+# Indeed calling this function with a vector argument returns a vector:
+
+rosenbrock_vector([1.0, 0.5])
+
+# By now, we should be quite familiar with the ForwarDiff interface and you might
+# even guess how we should compute the Jacobian:
+
+ForwardDiff.jacobian(rosenbrock_vector, [1.0, 0.5])
+
+# The Jacobian functionality could be used for example in [`NLsolve.jl`](https://github.com/JuliaNLSolvers/NLsolve.jl),
+# which is a nonlinear equation solver.
+
+# ### Summary `ForwardDiff`
+# This should get you started with using `ForwardDiff`. If your functions do not have too big vectors as
+# input arguments, the performance should be good. It will likely not beat a carefully tuned
+# analytical implementaion of the derivative but it is oftan that from a productivity point of view
+# it is worth using AD.
+
+# ## Revisediff
+#
+# ForwardDiff is using what is known as forward mode differentiation.
+# If the number of input parameters is large and the output is just a scalar
+# then reverse mode differentation is likely more effective.
+#
+# TODO..
+
+end #src
diff --git a/Courses/Differentiable Programming/060 Reverse Differentiation.jl b/Courses/Differentiable Programming/060 Reverse Differentiation.jl
new file mode 100644
index 0000000..e69de29
diff --git a/Courses/Differentiable Programming/Manifest.toml b/Courses/Differentiable Programming/Manifest.toml
new file mode 100644
index 0000000..9b3c023
--- /dev/null
+++ b/Courses/Differentiable Programming/Manifest.toml
@@ -0,0 +1,872 @@
+# This file is machine-generated - editing it directly is not advised
+
+[[AbstractTrees]]
+deps = ["Markdown", "Test"]
+git-tree-sha1 = "6621d9645702c1c4e6970cc6a3eae440c768000b"
+uuid = "1520ce14-60c1-5f80-bbc7-55ef81b5835c"
+version = "0.2.1"
+
+[[Adapt]]
+deps = ["LinearAlgebra", "Test"]
+git-tree-sha1 = "53d8fec4f662088c1202530e338a11a919407f3b"
+uuid = "79e6a3ab-5dfb-504d-930d-738a2a938a0e"
+version = "0.4.2"
+
+[[Arpack]]
+deps = ["BinaryProvider", "Libdl", "LinearAlgebra"]
+git-tree-sha1 = "07a2c077bdd4b6d23a40342a8a108e2ee5e58ab6"
+uuid = "7d9fca2a-8960-54d3-9f78-7d1dccf2cb97"
+version = "0.3.1"
+
+[[ArrayInterface]]
+deps = ["Requires", "Test"]
+git-tree-sha1 = "6a1a371393e56f5e8d5657fe4da4b11aea0bfbae"
+uuid = "4fba245c-0d91-5ea0-9b3e-6abc04ee57a9"
+version = "0.1.1"
+
+[[AssetRegistry]]
+deps = ["Distributed", "JSON", "Pidfile", "SHA", "Test"]
+git-tree-sha1 = "b25e88db7944f98789130d7b503276bc34bc098e"
+uuid = "bf4720bc-e11a-5d0c-854e-bdca1663c893"
+version = "0.1.0"
+
+[[BandedMatrices]]
+deps = ["FillArrays", "LazyArrays", "LinearAlgebra", "MatrixFactorizations", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "dd74592d0952af59b97e12d6f69bfc9cc3a79614"
+uuid = "aae01518-5342-5314-be14-df237901396f"
+version = "0.9.2"
+
+[[Base64]]
+uuid = "2a0f44e3-6c83-55bd-87e4-b1978d98bd5f"
+
+[[BenchmarkTools]]
+deps = ["JSON", "Printf", "Statistics", "Test"]
+git-tree-sha1 = "5d1dd8577643ba9014574cd40d9c028cd5e4b85a"
+uuid = "6e4b80f9-dd63-53aa-95a3-0cdb28fa8baf"
+version = "0.4.2"
+
+[[BinDeps]]
+deps = ["Compat", "Libdl", "SHA", "URIParser"]
+git-tree-sha1 = "12093ca6cdd0ee547c39b1870e0c9c3f154d9ca9"
+uuid = "9e28174c-4ba2-5203-b857-d8d62c4213ee"
+version = "0.8.10"
+
+[[BinaryProvider]]
+deps = ["Libdl", "Logging", "SHA"]
+git-tree-sha1 = "8153fd64131cd00a79544bb23788877741f627bb"
+uuid = "b99e7846-7c00-51b0-8f62-c81ae34c0232"
+version = "0.5.5"
+
+[[BoundaryValueDiffEq]]
+deps = ["BandedMatrices", "DiffEqBase", "DiffEqDiffTools", "ForwardDiff", "LinearAlgebra", "NLsolve", "Reexport", "SparseArrays", "Test"]
+git-tree-sha1 = "0f4a4f86ae63671efd9b41de9dea8ad993f2daad"
+uuid = "764a87c0-6b3e-53db-9096-fe964310641d"
+version = "2.2.3"
+
+[[CSTParser]]
+deps = ["Tokenize"]
+git-tree-sha1 = "376a39f1862000442011390f1edf5e7f4dcc7142"
+uuid = "00ebfdb7-1f24-5e51-bd34-a7502290713f"
+version = "0.6.0"
+
+[[CSV]]
+deps = ["CategoricalArrays", "DataFrames", "Dates", "Mmap", "Parsers", "PooledArrays", "Profile", "Tables", "Unicode", "WeakRefStrings"]
+git-tree-sha1 = "078801ccf5a644df31cef99c9add46107b94aba5"
+uuid = "336ed68f-0bac-5ca0-87d4-7b16caf5d00b"
+version = "0.5.6"
+
+[[Calculus]]
+deps = ["Compat"]
+git-tree-sha1 = "f60954495a7afcee4136f78d1d60350abd37a409"
+uuid = "49dc2e85-a5d0-5ad3-a950-438e2897f1b9"
+version = "0.4.1"
+
+[[CategoricalArrays]]
+deps = ["Compat", "Future", "JSON", "Missings", "Printf", "Reexport"]
+git-tree-sha1 = "26601961df6afacdd16d67c1eec6cfe75e5ae9ab"
+uuid = "324d7699-5711-5eae-9e2f-1d82baa6b597"
+version = "0.5.4"
+
+[[CodecZlib]]
+deps = ["BinaryProvider", "Libdl", "Test", "TranscodingStreams"]
+git-tree-sha1 = "36bbf5374c661054d41410dc53ff752972583b9b"
+uuid = "944b1d66-785c-5afd-91f1-9de20f533193"
+version = "0.5.2"
+
+[[ColorTypes]]
+deps = ["FixedPointNumbers", "Random"]
+git-tree-sha1 = "10050a24b09e8e41b951e9976b109871ce98d965"
+uuid = "3da002f7-5984-5a60-b8a6-cbb66c0b333f"
+version = "0.8.0"
+
+[[Colors]]
+deps = ["ColorTypes", "FixedPointNumbers", "InteractiveUtils", "Printf", "Reexport", "Test"]
+git-tree-sha1 = "9f0a0210450acb91c730b730a994f8eef1d3d543"
+uuid = "5ae59095-9a9b-59fe-a467-6f913c188581"
+version = "0.9.5"
+
+[[CommonSubexpressions]]
+deps = ["Test"]
+git-tree-sha1 = "efdaf19ab11c7889334ca247ff4c9f7c322817b0"
+uuid = "bbf7d656-a473-5ed7-a52c-81e309532950"
+version = "0.2.0"
+
+[[Compat]]
+deps = ["Base64", "Dates", "DelimitedFiles", "Distributed", "InteractiveUtils", "LibGit2", "Libdl", "LinearAlgebra", "Markdown", "Mmap", "Pkg", "Printf", "REPL", "Random", "Serialization", "SharedArrays", "Sockets", "SparseArrays", "Statistics", "Test", "UUIDs", "Unicode"]
+git-tree-sha1 = "84aa74986c5b9b898b0d1acaf3258741ee64754f"
+uuid = "34da2185-b29b-5c13-b0c7-acf172513d20"
+version = "2.1.0"
+
+[[Contour]]
+deps = ["LinearAlgebra", "StaticArrays", "Test"]
+git-tree-sha1 = "b974e164358fea753ef853ce7bad97afec15bb80"
+uuid = "d38c429a-6771-53c6-b99e-75d170b6e991"
+version = "0.5.1"
+
+[[Crayons]]
+deps = ["Test"]
+git-tree-sha1 = "f621b8ef51fd2004c7cf157ea47f027fdeac5523"
+uuid = "a8cc5b0e-0ffa-5ad4-8c14-923d3ee1735f"
+version = "4.0.0"
+
+[[DataFrames]]
+deps = ["CategoricalArrays", "Compat", "IteratorInterfaceExtensions", "Missings", "PooledArrays", "Printf", "REPL", "Reexport", "SortingAlgorithms", "Statistics", "StatsBase", "TableTraits", "Tables", "Unicode"]
+git-tree-sha1 = "7c0f86a01be0f77cc7f3f9096ed875f1217487e1"
+uuid = "a93c6f00-e57d-5684-b7b6-d8193f3e46c0"
+version = "0.18.4"
+
+[[DataStructures]]
+deps = ["InteractiveUtils", "OrderedCollections", "Random", "Serialization", "Test"]
+git-tree-sha1 = "ca971f03e146cf144a9e2f2ce59674f5bf0e8038"
+uuid = "864edb3b-99cc-5e75-8d2d-829cb0a9cfe8"
+version = "0.15.0"
+
+[[DataValueInterfaces]]
+git-tree-sha1 = "bfc1187b79289637fa0ef6d4436ebdfe6905cbd6"
+uuid = "e2d170a0-9d28-54be-80f0-106bbe20a464"
+version = "1.0.0"
+
+[[Dates]]
+deps = ["Printf"]
+uuid = "ade2ca70-3891-5945-98fb-dc099432e06a"
+
+[[DelayDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "ForwardDiff", "MuladdMacro", "NLSolversBase", "OrdinaryDiffEq", "RecursiveArrayTools", "Reexport", "Roots"]
+git-tree-sha1 = "d933682653f8c3c922592d75e50b5a30689ede6d"
+uuid = "bcd4f6db-9728-5f36-b5f7-82caef46ccdb"
+version = "5.4.1"
+
+[[DelimitedFiles]]
+deps = ["Mmap"]
+uuid = "8bb1440f-4735-579b-a4ab-409b98df4dab"
+
+[[DiffEqBase]]
+deps = ["Compat", "Distributed", "DocStringExtensions", "FunctionWrappers", "IterativeSolvers", "IteratorInterfaceExtensions", "LinearAlgebra", "MuladdMacro", "Parameters", "RecipesBase", "RecursiveArrayTools", "RecursiveFactorization", "Requires", "Roots", "SparseArrays", "StaticArrays", "Statistics", "SuiteSparse", "TableTraits", "TreeViews"]
+git-tree-sha1 = "3c08441014d2e1bad515df5443dd2d0ba379888c"
+uuid = "2b5f629d-d688-5b77-993f-72d75c75574e"
+version = "5.12.0"
+
+[[DiffEqCallbacks]]
+deps = ["DataStructures", "DiffEqBase", "LinearAlgebra", "OrdinaryDiffEq", "RecipesBase", "RecursiveArrayTools", "StaticArrays", "Test"]
+git-tree-sha1 = "027a13f010f2a93b2df725b7f6202590ce6f559d"
+uuid = "459566f4-90b8-5000-8ac3-15dfb0a30def"
+version = "2.5.2"
+
+[[DiffEqDiffTools]]
+deps = ["LinearAlgebra", "SparseArrays", "StaticArrays"]
+git-tree-sha1 = "2d4f49c1839c1f30e4820400d8c109c6b16e869a"
+uuid = "01453d9d-ee7c-5054-8395-0335cb756afa"
+version = "0.13.0"
+
+[[DiffEqFinancial]]
+deps = ["DiffEqBase", "DiffEqNoiseProcess", "LinearAlgebra", "Markdown", "RandomNumbers", "Test"]
+git-tree-sha1 = "f250512b982b771f6bdb3df05b89df314f2c2580"
+uuid = "5a0ffddc-d203-54b0-88ba-2c03c0fc2e67"
+version = "2.1.0"
+
+[[DiffEqFlux]]
+deps = ["Adapt", "DiffEqBase", "DiffEqSensitivity", "DiffResults", "Flux", "ForwardDiff", "RecursiveArrayTools", "Requires"]
+git-tree-sha1 = "1c311e6a4f14c70c7ea33482db9856392c4b6b80"
+uuid = "aae7a2af-3d4f-5e19-a356-7da93b79d9d0"
+version = "0.5.0"
+
+[[DiffEqJump]]
+deps = ["Compat", "DataStructures", "DiffEqBase", "FunctionWrappers", "LinearAlgebra", "Parameters", "PoissonRandom", "Random", "RandomNumbers", "RecursiveArrayTools", "Statistics", "Test", "TreeViews"]
+git-tree-sha1 = "784b979eeca8e9586aea9e63edbdcf5573bf9449"
+uuid = "c894b116-72e5-5b58-be3c-e6d8d4ac2b12"
+version = "6.1.1"
+
+[[DiffEqMonteCarlo]]
+deps = ["DiffEqBase", "Distributed", "RecursiveArrayTools", "StaticArrays", "Statistics"]
+git-tree-sha1 = "edffd3e114b5c2cad15e7790db6d82f69e3f42ae"
+uuid = "78ddff82-25fc-5f2b-89aa-309469cbf16f"
+version = "0.15.1"
+
+[[DiffEqNoiseProcess]]
+deps = ["DataStructures", "DiffEqBase", "LinearAlgebra", "Random", "RandomNumbers", "RecipesBase", "RecursiveArrayTools", "Requires", "ResettableStacks", "StaticArrays", "Statistics"]
+git-tree-sha1 = "f5333c0aa6208680e48cd24ae6f759c262a1cf85"
+uuid = "77a26b50-5914-5dd7-bc55-306e6241c503"
+version = "3.3.1"
+
+[[DiffEqOperators]]
+deps = ["DiffEqBase", "ForwardDiff", "LinearAlgebra", "SparseArrays", "StaticArrays", "SuiteSparse"]
+git-tree-sha1 = "2884a79a72aac38347b247615ac42eda41aa36e0"
+uuid = "9fdde737-9c7f-55bf-ade8-46b3f136cc48"
+version = "3.5.0"
+
+[[DiffEqPhysics]]
+deps = ["Dates", "DiffEqBase", "DiffEqCallbacks", "ForwardDiff", "LinearAlgebra", "Printf", "Random", "RecipesBase", "RecursiveArrayTools", "Reexport", "StaticArrays", "Test"]
+git-tree-sha1 = "d3dbc53318a6477f496ae2347db98c3ded36c486"
+uuid = "055956cb-9e8b-5191-98cc-73ae4a59e68a"
+version = "3.1.0"
+
+[[DiffEqSensitivity]]
+deps = ["DataFrames", "DiffEqBase", "DiffEqCallbacks", "DiffEqDiffTools", "Flux", "ForwardDiff", "GLM", "LinearAlgebra", "QuadGK", "RecursiveArrayTools", "Statistics"]
+git-tree-sha1 = "09c964dc242f295180dd99d89fb2f259927029ef"
+uuid = "41bf760c-e81c-5289-8e54-58b1f1f8abe2"
+version = "3.2.4"
+
+[[DiffResults]]
+deps = ["Compat", "StaticArrays"]
+git-tree-sha1 = "34a4a1e8be7bc99bc9c611b895b5baf37a80584c"
+uuid = "163ba53b-c6d8-5494-b064-1a9d43ac40c5"
+version = "0.0.4"
+
+[[DiffRules]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "dc0869fb2f5b23466b32ea799bd82c76480167f7"
+uuid = "b552c78f-8df3-52c6-915a-8e097449b14b"
+version = "0.0.10"
+
+[[DifferentialEquations]]
+deps = ["BoundaryValueDiffEq", "DelayDiffEq", "DiffEqBase", "DiffEqCallbacks", "DiffEqFinancial", "DiffEqJump", "DiffEqMonteCarlo", "DiffEqNoiseProcess", "DiffEqPhysics", "DimensionalPlotRecipes", "LinearAlgebra", "MultiScaleArrays", "OrdinaryDiffEq", "Random", "RecursiveArrayTools", "Reexport", "SteadyStateDiffEq", "StochasticDiffEq", "Sundials"]
+git-tree-sha1 = "e5b3ca6afe2a064bdfecba483999ee75d81750c6"
+uuid = "0c46a032-eb83-5123-abaf-570d42b7fbaa"
+version = "6.4.0"
+
+[[DimensionalPlotRecipes]]
+deps = ["LinearAlgebra", "RecipesBase", "Test"]
+git-tree-sha1 = "d348688f9a3d02c24455327231c450c272b7401c"
+uuid = "c619ae07-58cd-5f6d-b883-8f17bd6a98f9"
+version = "0.2.0"
+
+[[Distances]]
+deps = ["LinearAlgebra", "Printf", "Random", "Statistics", "Test"]
+git-tree-sha1 = "a135c7c062023051953141da8437ed74f89d767a"
+uuid = "b4f34e82-e78d-54a5-968a-f98e89d6e8f7"
+version = "0.8.0"
+
+[[Distributed]]
+deps = ["Random", "Serialization", "Sockets"]
+uuid = "8ba89e20-285c-5b6f-9357-94700520ee1b"
+
+[[Distributions]]
+deps = ["LinearAlgebra", "PDMats", "Printf", "QuadGK", "Random", "SpecialFunctions", "Statistics", "StatsBase", "StatsFuns"]
+git-tree-sha1 = "56a158bc0abe4af5d4027af2275fde484261ca6d"
+uuid = "31c24e10-a181-5473-b8eb-7969acd0382f"
+version = "0.19.2"
+
+[[DocStringExtensions]]
+deps = ["LibGit2", "Markdown", "Pkg", "Test"]
+git-tree-sha1 = "0513f1a8991e9d83255e0140aace0d0fc4486600"
+uuid = "ffbed154-4ef7-542d-bbb7-c09d3a79fcae"
+version = "0.8.0"
+
+[[ExponentialUtilities]]
+deps = ["LinearAlgebra", "Printf", "SparseArrays"]
+git-tree-sha1 = "85e1ce16aa9b98793df704e17e7a0ceadefe404f"
+uuid = "d4d017d3-3776-5f7e-afef-a10c40355c18"
+version = "1.5.1"
+
+[[FileWatching]]
+uuid = "7b1f6079-737a-58dc-b8bc-7a2ca5c1b5ee"
+
+[[FillArrays]]
+deps = ["LinearAlgebra", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "9ab8f76758cbabba8d7f103c51dce7f73fcf8e92"
+uuid = "1a297f60-69ca-5386-bcde-b61e274b549b"
+version = "0.6.3"
+
+[[FixedPointNumbers]]
+git-tree-sha1 = "d14a6fa5890ea3a7e5dcab6811114f132fec2b4b"
+uuid = "53c48c17-4a7d-5ca2-90c5-79b7896eea93"
+version = "0.6.1"
+
+[[Flux]]
+deps = ["AbstractTrees", "Adapt", "CodecZlib", "Colors", "DelimitedFiles", "Juno", "LinearAlgebra", "MacroTools", "NNlib", "Pkg", "Printf", "Random", "Reexport", "Requires", "SHA", "Statistics", "StatsBase", "Tracker", "ZipFile"]
+git-tree-sha1 = "08212989c2856f95f90709ea5fd824bd27b34514"
+uuid = "587475ba-b771-5e3f-ad9e-33799f191a9c"
+version = "0.8.3"
+
+[[ForwardDiff]]
+deps = ["CommonSubexpressions", "DiffResults", "DiffRules", "InteractiveUtils", "LinearAlgebra", "NaNMath", "Random", "SparseArrays", "SpecialFunctions", "StaticArrays", "Test"]
+git-tree-sha1 = "4c4d727f1b7e0092134fabfab6396b8945c1ea5b"
+repo-rev = "master"
+repo-url = "https://github.com/JuliaDiff/ForwardDiff.jl.git"
+uuid = "f6369f11-7733-5829-9624-2563aa707210"
+version = "0.10.3+"
+
+[[FunctionWrappers]]
+deps = ["Compat"]
+git-tree-sha1 = "49bf793ebd37db5adaa7ac1eae96c2c97ec86db5"
+uuid = "069b7b12-0de2-55c6-9aab-29f3d0a68a2e"
+version = "1.0.0"
+
+[[FunctionalCollections]]
+deps = ["Test"]
+git-tree-sha1 = "04cb9cfaa6ba5311973994fe3496ddec19b6292a"
+uuid = "de31a74c-ac4f-5751-b3fd-e18cd04993ca"
+version = "0.5.0"
+
+[[Future]]
+deps = ["Random"]
+uuid = "9fa8497b-333b-5362-9e8d-4d0656e87820"
+
+[[GLM]]
+deps = ["Distributions", "LinearAlgebra", "Printf", "Random", "Reexport", "SparseArrays", "SpecialFunctions", "Statistics", "StatsBase", "StatsFuns", "StatsModels"]
+git-tree-sha1 = "bb918f52a8e2131857ddac319033610bb3be35a4"
+uuid = "38e38edf-8417-5370-95a0-9cbb8c7f171a"
+version = "1.3.0"
+
+[[GR]]
+deps = ["Base64", "DelimitedFiles", "LinearAlgebra", "Pkg", "Printf", "Random", "Serialization", "Sockets", "Test"]
+git-tree-sha1 = "9dff2d231311da78648abfa3287e3458a578d2f8"
+uuid = "28b8d3ca-fb5f-59d9-8090-bfdbd6d07a71"
+version = "0.40.0"
+
+[[GenericSVD]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "8aa93c3f3d81562a8962047eafcc5712af0a0f59"
+uuid = "01680d73-4ee2-5a08-a1aa-533608c188bb"
+version = "0.2.1"
+
+[[GeometryTypes]]
+deps = ["ColorTypes", "FixedPointNumbers", "IterTools", "LinearAlgebra", "StaticArrays"]
+git-tree-sha1 = "2b0bfb379a54bdfcd2942f388f7d045f8952373d"
+uuid = "4d00f742-c7ba-57c2-abde-4428a4b178cb"
+version = "0.7.5"
+
+[[HTTP]]
+deps = ["Base64", "Dates", "IniFile", "MbedTLS", "Sockets"]
+git-tree-sha1 = "6e59e7ec3c71eda9e0261c98896da5d3d008fa7d"
+uuid = "cd3eb016-35fb-5094-929b-558a96fad6f3"
+version = "0.8.3"
+
+[[IRTools]]
+deps = ["InteractiveUtils", "MacroTools", "Test"]
+git-tree-sha1 = "a9b1fc7745ae4745a634bbb6d1cb7fd64e37248a"
+uuid = "7869d1d1-7146-5819-86e3-90919afe41df"
+version = "0.2.2"
+
+[[IniFile]]
+deps = ["Test"]
+git-tree-sha1 = "098e4d2c533924c921f9f9847274f2ad89e018b8"
+uuid = "83e8ac13-25f8-5344-8a64-a9f2b223428f"
+version = "0.5.0"
+
+[[InteractiveUtils]]
+deps = ["Markdown"]
+uuid = "b77e0a4c-d291-57a0-90e8-8db25a27a240"
+
+[[IterTools]]
+deps = ["SparseArrays", "Test"]
+git-tree-sha1 = "79246285c43602384e6f1943b3554042a3712056"
+uuid = "c8e1da08-722c-5040-9ed9-7db0dc04731e"
+version = "1.1.1"
+
+[[IterativeSolvers]]
+deps = ["LinearAlgebra", "Printf", "Random", "RecipesBase", "SparseArrays", "Test"]
+git-tree-sha1 = "5687f68018b4f14c0da54d402bb23eecaec17f37"
+uuid = "42fd0dbc-a981-5370-80f2-aaf504508153"
+version = "0.8.1"
+
+[[IteratorInterfaceExtensions]]
+git-tree-sha1 = "a3f24677c21f5bbe9d2a714f95dcd58337fb2856"
+uuid = "82899510-4779-5014-852e-03e436cf321d"
+version = "1.0.0"
+
+[[JSExpr]]
+deps = ["JSON", "MacroTools", "Observables", "Test", "WebIO"]
+git-tree-sha1 = "013bc2143a2e84ea489365cf30db3407deb540c2"
+uuid = "97c1335a-c9c5-57fe-bc5d-ec35cebe8660"
+version = "0.5.0"
+
+[[JSON]]
+deps = ["Dates", "Distributed", "Mmap", "Sockets", "Test", "Unicode"]
+git-tree-sha1 = "1f7a25b53ec67f5e9422f1f551ee216503f4a0fa"
+uuid = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
+version = "0.20.0"
+
+[[Juno]]
+deps = ["Base64", "Logging", "Media", "Profile", "Test"]
+git-tree-sha1 = "4e4a8d43aa7ecec66cadaf311fbd1e5c9d7b9175"
+uuid = "e5e0dc1b-0480-54bc-9374-aad01c23163d"
+version = "0.7.0"
+
+[[LazyArrays]]
+deps = ["FillArrays", "LinearAlgebra", "MacroTools", "StaticArrays", "Test"]
+git-tree-sha1 = "5eec856c454496abe8f4504227fcc187205a502a"
+uuid = "5078a376-72f3-5289-bfd5-ec5146d43c02"
+version = "0.9.0"
+
+[[LibGit2]]
+uuid = "76f85450-5226-5b5a-8eaa-529ad045b433"
+
+[[Libdl]]
+uuid = "8f399da3-3557-5675-b5ff-fb832c97cbdb"
+
+[[LineSearches]]
+deps = ["LinearAlgebra", "NLSolversBase", "NaNMath", "Parameters", "Printf", "Test"]
+git-tree-sha1 = "54eb90e8dbe745d617c78dee1d6ae95c7f6f5779"
+uuid = "d3d80556-e9d4-5f37-9878-2ab0fcc64255"
+version = "7.0.1"
+
+[[LinearAlgebra]]
+deps = ["Libdl"]
+uuid = "37e2e46d-f89d-539d-b4ee-838fcccc9c8e"
+
+[[Literate]]
+deps = ["Base64", "JSON", "REPL", "Test"]
+git-tree-sha1 = "021e2e3106713e22a7f3769ebf9f2f4469670444"
+uuid = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
+version = "1.1.0"
+
+[[Logging]]
+uuid = "56ddb016-857b-54e1-b83d-db4d58db5568"
+
+[[MacroTools]]
+deps = ["CSTParser", "Compat", "DataStructures", "Test"]
+git-tree-sha1 = "daecd9e452f38297c686eba90dba2a6d5da52162"
+uuid = "1914dd2f-81c6-5fcd-8719-6d5c9610ff09"
+version = "0.5.0"
+
+[[Markdown]]
+deps = ["Base64"]
+uuid = "d6f4376e-aef5-505a-96c1-9c027394607a"
+
+[[MatrixFactorizations]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "cebc71d929a846dda61400f1cf3ba69c7e75fa63"
+uuid = "a3b82374-2e81-5b9e-98ce-41277c0e4c87"
+version = "0.0.4"
+
+[[MbedTLS]]
+deps = ["BinaryProvider", "Dates", "Libdl", "Random", "Sockets"]
+git-tree-sha1 = "85f5947b53c8cfd53ccfa3f4abae31faa22c2181"
+uuid = "739be429-bea8-5141-9913-cc70e7f3736d"
+version = "0.7.0"
+
+[[Measures]]
+deps = ["Test"]
+git-tree-sha1 = "ddfd6d13e330beacdde2c80de27c1c671945e7d9"
+uuid = "442fdcdd-2543-5da2-b0f3-8c86c306513e"
+version = "0.3.0"
+
+[[Media]]
+deps = ["MacroTools", "Test"]
+git-tree-sha1 = "75a54abd10709c01f1b86b84ec225d26e840ed58"
+uuid = "e89f7d12-3494-54d1-8411-f7d8b9ae1f27"
+version = "0.5.0"
+
+[[Missings]]
+deps = ["SparseArrays", "Test"]
+git-tree-sha1 = "f0719736664b4358aa9ec173077d4285775f8007"
+uuid = "e1d29d7a-bbdc-5cf2-9ac0-f12de2c33e28"
+version = "0.4.1"
+
+[[Mmap]]
+uuid = "a63ad114-7e13-5084-954f-fe012c677804"
+
+[[MuladdMacro]]
+deps = ["MacroTools", "Test"]
+git-tree-sha1 = "41e6e7c4b448afeaddaac7f496b414854f83b848"
+uuid = "46d2c3a1-f734-5fdb-9937-b9b9aeba4221"
+version = "0.2.1"
+
+[[MultiScaleArrays]]
+deps = ["DiffEqBase", "LinearAlgebra", "RecursiveArrayTools", "Statistics", "StochasticDiffEq", "Test", "TreeViews"]
+git-tree-sha1 = "4220ceea71186db2bb45cb817984c99e563f3662"
+uuid = "f9640e96-87f6-5992-9c3b-0743c6a49ffa"
+version = "1.4.0"
+
+[[NLSolversBase]]
+deps = ["Calculus", "DiffEqDiffTools", "DiffResults", "Distributed", "ForwardDiff", "LinearAlgebra", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "0c6f0e7f2178f78239cfb75310359eed10f2cacb"
+uuid = "d41bc354-129a-5804-8e4c-c37616107c6c"
+version = "7.3.1"
+
+[[NLsolve]]
+deps = ["DiffEqDiffTools", "Distances", "ForwardDiff", "LineSearches", "LinearAlgebra", "NLSolversBase", "Printf", "Random", "Reexport", "SparseArrays", "Test"]
+git-tree-sha1 = "413e54f04a4cbe9804089794eec6b06b2a43bc47"
+uuid = "2774e3e8-f4cf-5e23-947b-6d7e65073b56"
+version = "4.0.0"
+
+[[NNlib]]
+deps = ["Libdl", "LinearAlgebra", "Requires", "Statistics", "TimerOutputs"]
+git-tree-sha1 = "0c667371391fc6bb31f7f12f96a56a17098b3de8"
+uuid = "872c559c-99b0-510c-b3b7-b6c96a88d5cd"
+version = "0.6.0"
+
+[[NaNMath]]
+deps = ["Compat"]
+git-tree-sha1 = "ce3b85e484a5d4c71dd5316215069311135fa9f2"
+uuid = "77ba4419-2d1f-58cd-9bb1-8ffee604a2e3"
+version = "0.3.2"
+
+[[Observables]]
+deps = ["Test"]
+git-tree-sha1 = "dc02cec22747d1d10d9f70d8a1c03432b5bfbcd0"
+uuid = "510215fc-4207-5dde-b226-833fc4488ee2"
+version = "0.2.3"
+
+[[OffsetArrays]]
+git-tree-sha1 = "1af2f79c7eaac3e019a0de41ef63335ff26a0a57"
+uuid = "6fe1bfb0-de20-5000-8ca7-80f57d26f881"
+version = "0.11.1"
+
+[[Optim]]
+deps = ["Calculus", "DiffEqDiffTools", "ForwardDiff", "LineSearches", "LinearAlgebra", "NLSolversBase", "NaNMath", "Parameters", "PositiveFactorizations", "Printf", "Random", "SparseArrays", "StatsBase", "Test"]
+git-tree-sha1 = "a626e09c1f7f019b8f3a30a8172c7b82d2f4810b"
+uuid = "429524aa-4258-5aef-a3af-852621145aeb"
+version = "0.18.1"
+
+[[OrderedCollections]]
+deps = ["Random", "Serialization", "Test"]
+git-tree-sha1 = "c4c13474d23c60d20a67b217f1d7f22a40edf8f1"
+uuid = "bac558e1-5e72-5ebc-8fee-abe8a469f55d"
+version = "1.1.0"
+
+[[OrdinaryDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "DiffEqOperators", "ExponentialUtilities", "ForwardDiff", "GenericSVD", "LinearAlgebra", "Logging", "MuladdMacro", "NLsolve", "Parameters", "RecursiveArrayTools", "Reexport", "StaticArrays"]
+git-tree-sha1 = "7481f05badc75b80a62d0da988f09d6028c4fbb1"
+uuid = "1dea7af3-3e70-54e6-95c3-0bf5283fa5ed"
+version = "5.8.1"
+
+[[PDMats]]
+deps = ["Arpack", "LinearAlgebra", "SparseArrays", "SuiteSparse", "Test"]
+git-tree-sha1 = "8b68513175b2dc4023a564cb0e917ce90e74fd69"
+uuid = "90014a1f-27ba-587c-ab20-58faa44d9150"
+version = "0.9.7"
+
+[[Parameters]]
+deps = ["Markdown", "OrderedCollections", "REPL", "Test"]
+git-tree-sha1 = "70bdbfb2bceabb15345c0b54be4544813b3444e4"
+uuid = "d96e819e-fc66-5662-9728-84c9c7592b0a"
+version = "0.10.3"
+
+[[Parsers]]
+deps = ["Dates", "Test"]
+git-tree-sha1 = "db2b35dedab3c0e46dc15996d170af07a5ab91c9"
+uuid = "69de0a69-1ddd-5017-9359-2bf0b02dc9f0"
+version = "0.3.6"
+
+[[Pidfile]]
+deps = ["FileWatching", "Test"]
+git-tree-sha1 = "1ffd82728498b5071cde851bbb7abd780d4445f3"
+uuid = "fa939f87-e72e-5be4-a000-7fc836dbe307"
+version = "1.1.0"
+
+[[Pkg]]
+deps = ["Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "UUIDs"]
+uuid = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
+
+[[PlotThemes]]
+deps = ["PlotUtils", "Requires", "Test"]
+git-tree-sha1 = "f3afd2d58e1f6ac9be2cea46e4a9083ccc1d990b"
+uuid = "ccf2f8ad-2431-5c83-bf29-c5338b663b6a"
+version = "0.3.0"
+
+[[PlotUtils]]
+deps = ["Colors", "Dates", "Printf", "Random", "Reexport", "Test"]
+git-tree-sha1 = "8e87bbb778c26f575fbe47fd7a49c7b5ca37c0c6"
+uuid = "995b91a9-d308-5afd-9ec6-746e21dbc043"
+version = "0.5.8"
+
+[[Plots]]
+deps = ["Base64", "Contour", "Dates", "FixedPointNumbers", "GR", "GeometryTypes", "JSON", "LinearAlgebra", "Measures", "NaNMath", "Pkg", "PlotThemes", "PlotUtils", "Printf", "REPL", "Random", "RecipesBase", "Reexport", "Requires", "Showoff", "SparseArrays", "Statistics", "StatsBase", "UUIDs"]
+git-tree-sha1 = "c446e51959578de01b5a4efa72ca6f2460e38196"
+uuid = "91a5bcdd-55d7-5caf-9e0b-520d859cae80"
+version = "0.25.1"
+
+[[PoissonRandom]]
+deps = ["Random", "Statistics", "Test"]
+git-tree-sha1 = "44d018211a56626288b5d3f8c6497d28c26dc850"
+uuid = "e409e4f3-bfea-5376-8464-e040bb5c01ab"
+version = "0.4.0"
+
+[[PooledArrays]]
+git-tree-sha1 = "6e8c38927cb6e9ae144f7277c753714861b27d14"
+uuid = "2dfb63ee-cc39-5dd5-95bd-886bf059d720"
+version = "0.5.2"
+
+[[PositiveFactorizations]]
+deps = ["LinearAlgebra", "Test"]
+git-tree-sha1 = "957c3dd7c33895469760ce873082fbb6b3620641"
+uuid = "85a6dd25-e78a-55b7-8502-1745935b8125"
+version = "0.2.2"
+
+[[Printf]]
+deps = ["Unicode"]
+uuid = "de0858da-6303-5e67-8744-51eddeeeb8d7"
+
+[[Profile]]
+deps = ["Printf"]
+uuid = "9abbd945-dff8-562f-b5e8-e1ebf5ef1b79"
+
+[[QuadGK]]
+deps = ["DataStructures", "LinearAlgebra"]
+git-tree-sha1 = "438630b843c210b375b2a246329200c113acc61b"
+uuid = "1fd47b50-473d-5c70-9696-f719f8f3bcdc"
+version = "2.1.0"
+
+[[REPL]]
+deps = ["InteractiveUtils", "Markdown", "Sockets"]
+uuid = "3fa0cd96-eef1-5676-8a61-b3b8758bbffb"
+
+[[Random]]
+deps = ["Serialization"]
+uuid = "9a3f8284-a2c9-5f02-9a11-845980a1fd5c"
+
+[[RandomNumbers]]
+deps = ["Random", "Requires"]
+git-tree-sha1 = "1417be19c15706c1584d01e32662eb640a4cc908"
+uuid = "e6cf234a-135c-5ec9-84dd-332b85af5143"
+version = "1.3.0"
+
+[[RecipesBase]]
+git-tree-sha1 = "7bdce29bc9b2f5660a6e5e64d64d91ec941f6aa2"
+uuid = "3cdcf5f2-1ef4-517c-9805-6587b60abb01"
+version = "0.7.0"
+
+[[RecursiveArrayTools]]
+deps = ["ArrayInterface", "RecipesBase", "Requires", "StaticArrays", "Statistics", "Test"]
+git-tree-sha1 = "187ea7dd541955102c7035a6668613bdf52022ca"
+uuid = "731186ca-8d62-57ce-b412-fbd966d074cd"
+version = "0.20.0"
+
+[[RecursiveFactorization]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "54410ebd72cbb84d7b7678eb3da643f8e71181fc"
+uuid = "f2c3362d-daeb-58d1-803e-2bc74f2840b4"
+version = "0.0.1"
+
+[[Reexport]]
+deps = ["Pkg"]
+git-tree-sha1 = "7b1d07f411bc8ddb7977ec7f377b97b158514fe0"
+uuid = "189a3867-3050-52da-a836-e630ba90ab69"
+version = "0.2.0"
+
+[[Requires]]
+deps = ["Test"]
+git-tree-sha1 = "f6fbf4ba64d295e146e49e021207993b6b48c7d1"
+uuid = "ae029012-a4dd-5104-9daa-d747884805df"
+version = "0.5.2"
+
+[[ResettableStacks]]
+deps = ["Random", "StaticArrays", "Test"]
+git-tree-sha1 = "8b4f6cf3c97530e1ba7177ad3bc2b134373da851"
+uuid = "ae5879a3-cd67-5da8-be7f-38c6eb64a37b"
+version = "0.6.0"
+
+[[Rmath]]
+deps = ["BinaryProvider", "Libdl", "Random", "Statistics", "Test"]
+git-tree-sha1 = "9a6c758cdf73036c3239b0afbea790def1dabff9"
+uuid = "79098fc4-a85e-5d69-aa6a-4863f24498fa"
+version = "0.5.0"
+
+[[Roots]]
+deps = ["Printf", "Statistics", "Test"]
+git-tree-sha1 = "7228278e31d6d0e22a1ae0b41ea9a0df2859f33d"
+uuid = "f2b01f46-fcfa-551c-844a-d8ac1e96c665"
+version = "0.8.1"
+
+[[SHA]]
+uuid = "ea8e919c-243c-51af-8825-aaa63cd721ce"
+
+[[Serialization]]
+uuid = "9e88b42a-f829-5b0c-bbe9-9e923198166b"
+
+[[SharedArrays]]
+deps = ["Distributed", "Mmap", "Random", "Serialization"]
+uuid = "1a1011a3-84de-559e-8e89-a11a2f7dc383"
+
+[[ShiftedArrays]]
+deps = ["OffsetArrays", "RecursiveArrayTools", "Test"]
+git-tree-sha1 = "b1aa84666a23a31cebcdcb848e62428968789287"
+uuid = "1277b4bf-5013-50f5-be3d-901d8477a67a"
+version = "0.5.0"
+
+[[Showoff]]
+deps = ["Dates"]
+git-tree-sha1 = "e032c9df551fb23c9f98ae1064de074111b7bc39"
+uuid = "992d4aef-0814-514b-bc4d-f2e9a6c4116f"
+version = "0.3.1"
+
+[[Sockets]]
+uuid = "6462fe0b-24de-5631-8697-dd941f90decc"
+
+[[SortingAlgorithms]]
+deps = ["DataStructures", "Random", "Test"]
+git-tree-sha1 = "03f5898c9959f8115e30bc7226ada7d0df554ddd"
+uuid = "a2af1166-a08f-5f64-846c-94a0d3cef48c"
+version = "0.3.1"
+
+[[SparseArrays]]
+deps = ["LinearAlgebra", "Random"]
+uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
+
+[[SpecialFunctions]]
+deps = ["BinDeps", "BinaryProvider", "Libdl", "Test"]
+git-tree-sha1 = "0b45dc2e45ed77f445617b99ff2adf0f5b0f23ea"
+uuid = "276daf66-3868-5448-9aa4-cd146d93841b"
+version = "0.7.2"
+
+[[StaticArrays]]
+deps = ["LinearAlgebra", "Random", "Statistics"]
+git-tree-sha1 = "db23bbf50064c582b6f2b9b043c8e7e98ea8c0c6"
+uuid = "90137ffa-7385-5640-81b9-e52037218182"
+version = "0.11.0"
+
+[[Statistics]]
+deps = ["LinearAlgebra", "SparseArrays"]
+uuid = "10745b16-79ce-11e8-11f9-7d13ad32a3b2"
+
+[[StatsBase]]
+deps = ["DataStructures", "LinearAlgebra", "Missings", "Printf", "Random", "SortingAlgorithms", "SparseArrays", "Statistics"]
+git-tree-sha1 = "8a0f4b09c7426478ab677245ab2b0b68552143c7"
+uuid = "2913bbd2-ae8a-5f71-8c99-4fb6c76f3a91"
+version = "0.30.0"
+
+[[StatsFuns]]
+deps = ["Rmath", "SpecialFunctions", "Test"]
+git-tree-sha1 = "b3a4e86aa13c732b8a8c0ba0c3d3264f55e6bb3e"
+uuid = "4c63d2b9-4356-54db-8cca-17b64c39e42c"
+version = "0.8.0"
+
+[[StatsModels]]
+deps = ["CategoricalArrays", "DataStructures", "LinearAlgebra", "Missings", "ShiftedArrays", "SparseArrays", "StatsBase", "Tables"]
+git-tree-sha1 = "f004c23db67aeecb4bba94d08c79580af851b21b"
+uuid = "3eaba693-59b7-5ba5-a881-562e759f1c8d"
+version = "0.6.1"
+
+[[SteadyStateDiffEq]]
+deps = ["Compat", "DiffEqBase", "DiffEqCallbacks", "LinearAlgebra", "NLsolve", "Reexport", "Test"]
+git-tree-sha1 = "fe9852d18c3e30f384003da50d6049e5fbc97071"
+uuid = "9672c7b4-1e72-59bd-8a11-6ac3964bc41f"
+version = "1.4.0"
+
+[[StochasticDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "DiffEqNoiseProcess", "DiffEqOperators", "FillArrays", "ForwardDiff", "LinearAlgebra", "Logging", "MuladdMacro", "NLsolve", "Parameters", "Random", "RandomNumbers", "RecursiveArrayTools", "Reexport", "StaticArrays"]
+git-tree-sha1 = "83be179dc849f11f83dcfa715c7818ef551a0f6c"
+uuid = "789caeaf-c7a9-5a7d-9973-96adeb23e2a0"
+version = "6.5.0"
+
+[[SuiteSparse]]
+deps = ["Libdl", "LinearAlgebra", "Serialization", "SparseArrays"]
+uuid = "4607b0f0-06f3-5cda-b6b1-a6196a1729e9"
+
+[[Sundials]]
+deps = ["BinaryProvider", "DataStructures", "DiffEqBase", "Libdl", "LinearAlgebra", "Logging", "Reexport", "SparseArrays", "SuiteSparse"]
+git-tree-sha1 = "9af4eb72683f0dafe84c6a5bd31aea1ebca4d46c"
+uuid = "c3572dad-4567-51f8-b174-8c6c989267f4"
+version = "3.6.1"
+
+[[TableTraits]]
+deps = ["IteratorInterfaceExtensions"]
+git-tree-sha1 = "b1ad568ba658d8cbb3b892ed5380a6f3e781a81e"
+uuid = "3783bdb8-4a98-5b6b-af9a-565f29a5fe9c"
+version = "1.0.0"
+
+[[Tables]]
+deps = ["DataValueInterfaces", "IteratorInterfaceExtensions", "LinearAlgebra", "Requires", "TableTraits", "Test"]
+git-tree-sha1 = "c93aafd5c45f850c653ec1c45857ba2151835f95"
+uuid = "bd369af6-aec1-5ad0-b16a-f7cc5008161c"
+version = "0.2.7"
+
+[[Test]]
+deps = ["Distributed", "InteractiveUtils", "Logging", "Random"]
+uuid = "8dfed614-e22c-5e08-85e1-65c5234f0b40"
+
+[[TimerOutputs]]
+deps = ["Crayons", "Printf", "Test", "Unicode"]
+git-tree-sha1 = "b80671c06f8f8bae08c55d67b5ce292c5ae2660c"
+uuid = "a759f4b9-e2f1-59dc-863e-4aeb61b1ea8f"
+version = "0.5.0"
+
+[[Tokenize]]
+git-tree-sha1 = "0de343efc07da00cd449d5b04e959ebaeeb3305d"
+uuid = "0796e94c-ce3b-5d07-9a54-7f471281c624"
+version = "0.5.4"
+
+[[Tracker]]
+deps = ["Adapt", "DiffRules", "ForwardDiff", "LinearAlgebra", "MacroTools", "NNlib", "NaNMath", "Printf", "Random", "Requires", "SpecialFunctions", "Statistics", "Test"]
+git-tree-sha1 = "327342fec6e09f68ced0c2dc5731ed475e4b696b"
+uuid = "9f7883ad-71c0-57eb-9f7f-b5c9e6d3789c"
+version = "0.2.2"
+
+[[TranscodingStreams]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "a25d8e5a28c3b1b06d3859f30757d43106791919"
+uuid = "3bb67fe8-82b1-5028-8e26-92a6c54297fa"
+version = "0.9.4"
+
+[[Trebuchet]]
+deps = ["DiffEqBase", "JSExpr", "OrdinaryDiffEq", "WebIO"]
+git-tree-sha1 = "c1daf264ca0c050381be6258b5e311615ea5f250"
+uuid = "98b73d46-197d-11e9-11eb-69a6ff759d3a"
+version = "0.1.0"
+
+[[TreeViews]]
+deps = ["Test"]
+git-tree-sha1 = "8d0d7a3fe2f30d6a7f833a5f19f7c7a5b396eae6"
+uuid = "a2a6695c-b41b-5b7d-aed9-dbfdeacea5d7"
+version = "0.3.0"
+
+[[URIParser]]
+deps = ["Test", "Unicode"]
+git-tree-sha1 = "6ddf8244220dfda2f17539fa8c9de20d6c575b69"
+uuid = "30578b45-9adc-5946-b283-645ec420af67"
+version = "0.4.0"
+
+[[UUIDs]]
+deps = ["Random", "SHA"]
+uuid = "cf7118a7-6976-5b1a-9a39-7adc72f591a4"
+
+[[Unicode]]
+uuid = "4ec0a83e-493e-50e2-b9ac-8f72acf5a8f5"
+
+[[WeakRefStrings]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "9a0bb82eede528debe631b642eeb48a631a69bc2"
+uuid = "ea10d353-3f73-51f8-a26c-33c1cb351aa5"
+version = "0.6.1"
+
+[[WebIO]]
+deps = ["AssetRegistry", "Base64", "Compat", "Distributed", "FunctionalCollections", "JSON", "Logging", "Observables", "Random", "Requires", "Sockets", "UUIDs", "WebSockets", "Widgets"]
+git-tree-sha1 = "458ebbd85da851b01bed01e6321b0d8f4c7044b0"
+uuid = "0f1e0344-ec1d-5b48-a673-e5cf874b6c29"
+version = "0.8.6"
+
+[[WebSockets]]
+deps = ["Base64", "Dates", "Distributed", "HTTP", "Logging", "Random", "Sockets", "Test"]
+git-tree-sha1 = "13f763d38c7a05688938808b49cb29b18b60c8c8"
+uuid = "104b5d7c-a370-577a-8038-80a2059c5097"
+version = "1.5.2"
+
+[[Widgets]]
+deps = ["Colors", "Dates", "Observables", "OrderedCollections", "Test"]
+git-tree-sha1 = "c53befc70c6b91eaa2a9888c2f6ac2d92720a81b"
+uuid = "cc8bc4a8-27d6-5769-a93b-9d913e69aa62"
+version = "0.6.1"
+
+[[ZipFile]]
+deps = ["BinaryProvider", "Libdl", "Printf"]
+git-tree-sha1 = "580ce62b6c14244916cc28ad54f8a2e2886f843d"
+uuid = "a5390f91-8eb1-5f08-bee0-b1d1ffed6cea"
+version = "0.8.3"
+
+[[Zygote]]
+deps = ["DiffRules", "FillArrays", "ForwardDiff", "IRTools", "InteractiveUtils", "LinearAlgebra", "MacroTools", "NNlib", "NaNMath", "Random", "Requires", "SpecialFunctions", "Statistics"]
+git-tree-sha1 = "520d65c5e5554473863d738bde053f5f6769d3be"
+uuid = "e88e6eb3-aa80-5325-afca-941959d7151f"
+version = "0.3.2"
diff --git a/Courses/Differentiable Programming/Project.toml b/Courses/Differentiable Programming/Project.toml
new file mode 100644
index 0000000..3c94cc3
--- /dev/null
+++ b/Courses/Differentiable Programming/Project.toml
@@ -0,0 +1,12 @@
+[deps]
+BenchmarkTools = "6e4b80f9-dd63-53aa-95a3-0cdb28fa8baf"
+CSV = "336ed68f-0bac-5ca0-87d4-7b16caf5d00b"
+DiffEqFlux = "aae7a2af-3d4f-5e19-a356-7da93b79d9d0"
+DifferentialEquations = "0c46a032-eb83-5123-abaf-570d42b7fbaa"
+Flux = "587475ba-b771-5e3f-ad9e-33799f191a9c"
+ForwardDiff = "f6369f11-7733-5829-9624-2563aa707210"
+Literate = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
+Optim = "429524aa-4258-5aef-a3af-852621145aeb"
+Plots = "91a5bcdd-55d7-5caf-9e0b-520d859cae80"
+Trebuchet = "98b73d46-197d-11e9-11eb-69a6ff759d3a"
+Zygote = "e88e6eb3-aa80-5325-afca-941959d7151f"
diff --git a/Manifest.toml b/Manifest.toml
index fb2c933..d0f2265 100644
--- a/Manifest.toml
+++ b/Manifest.toml
@@ -4,8 +4,10 @@
uuid = "2a0f44e3-6c83-55bd-87e4-b1978d98bd5f"
[[BinaryProvider]]
-deps = ["Compat", "CredentialsHandler", "Libdl", "Pkg", "SHA", "TOML", "Test"]
+deps = ["Libdl", "Logging", "SHA"]
+git-tree-sha1 = "8153fd64131cd00a79544bb23788877741f627bb"
uuid = "b99e7846-7c00-51b0-8f62-c81ae34c0232"
+version = "0.5.5"
[[Compat]]
deps = ["Base64", "Dates", "DelimitedFiles", "Distributed", "InteractiveUtils", "LibGit2", "Libdl", "LinearAlgebra", "Markdown", "Mmap", "Pkg", "Printf", "REPL", "Random", "Serialization", "SharedArrays", "Sockets", "SparseArrays", "Statistics", "Test", "UUIDs", "Unicode"]
@@ -13,9 +15,11 @@ git-tree-sha1 = "84aa74986c5b9b898b0d1acaf3258741ee64754f"
uuid = "34da2185-b29b-5c13-b0c7-acf172513d20"
version = "2.1.0"
-[[CredentialsHandler]]
-deps = ["Base64", "HTTP", "TOML"]
-uuid = "864e158e-919d-11e8-198e-cfe890ec4681"
+[[Conda]]
+deps = ["JSON", "VersionParsing"]
+git-tree-sha1 = "9a11d428dcdc425072af4aea19ab1e8c3e01c032"
+uuid = "8f4d0f93-b110-5947-807f-2305c1781a2d"
+version = "1.3.0"
[[Dates]]
deps = ["Printf"]
@@ -26,18 +30,26 @@ deps = ["Mmap"]
uuid = "8bb1440f-4735-579b-a4ab-409b98df4dab"
[[Distributed]]
-deps = ["LinearAlgebra", "Random", "Serialization", "Sockets"]
+deps = ["Random", "Serialization", "Sockets"]
uuid = "8ba89e20-285c-5b6f-9357-94700520ee1b"
-[[HTTP]]
-deps = ["Base64", "Dates", "Distributed", "IniFile", "MbedTLS", "Sockets", "Test"]
-uuid = "cd3eb016-35fb-5094-929b-558a96fad6f3"
+[[FileWatching]]
+uuid = "7b1f6079-737a-58dc-b8bc-7a2ca5c1b5ee"
-[[IniFile]]
-uuid = "83e8ac13-25f8-5344-8a64-a9f2b223428f"
+[[Glob]]
+deps = ["Compat", "Test"]
+git-tree-sha1 = "c72f1fcb7d17426de1e8af2e948dfb3de1116eed"
+uuid = "c27321d9-0574-5035-807b-f59d2c89b15c"
+version = "1.2.0"
+
+[[IJulia]]
+deps = ["Base64", "Conda", "Dates", "InteractiveUtils", "JSON", "Markdown", "MbedTLS", "Pkg", "Printf", "REPL", "Random", "SoftGlobalScope", "Test", "UUIDs", "ZMQ"]
+git-tree-sha1 = "8eb8459d806de665f1347b25e9ad9428c2609f0f"
+uuid = "7073ff75-c697-5162-941a-fcdaad2a7d2a"
+version = "1.18.1"
[[InteractiveUtils]]
-deps = ["LinearAlgebra", "Markdown"]
+deps = ["Markdown"]
uuid = "b77e0a4c-d291-57a0-90e8-8db25a27a240"
[[JSON]]
@@ -46,14 +58,6 @@ git-tree-sha1 = "1f7a25b53ec67f5e9422f1f551ee216503f4a0fa"
uuid = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
version = "0.20.0"
-[[JuliaAcademyData]]
-deps = ["Pkg"]
-git-tree-sha1 = "6cc6db29d6560619be88d0075d697047eb484f92"
-repo-rev = "master"
-repo-url = "https://github.com/JuliaComputing/JuliaAcademyData.jl"
-uuid = "18b7da76-0988-5e3b-acac-6290be3a708f"
-version = "0.1.0"
-
[[LibGit2]]
uuid = "76f85450-5226-5b5a-8eaa-529ad045b433"
@@ -78,14 +82,16 @@ deps = ["Base64"]
uuid = "d6f4376e-aef5-505a-96c1-9c027394607a"
[[MbedTLS]]
-deps = ["BinaryProvider", "Dates", "Libdl", "Pkg", "Random", "Sockets"]
+deps = ["BinaryProvider", "Dates", "Distributed", "Libdl", "Random", "Sockets", "Test"]
+git-tree-sha1 = "2d94286a9c2f52c63a16146bb86fd6cdfbf677c6"
uuid = "739be429-bea8-5141-9913-cc70e7f3736d"
+version = "0.6.8"
[[Mmap]]
uuid = "a63ad114-7e13-5084-954f-fe012c677804"
[[Pkg]]
-deps = ["BinaryProvider", "CredentialsHandler", "Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "TOML", "UUIDs"]
+deps = ["Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "UUIDs"]
uuid = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
[[Printf]]
@@ -113,6 +119,12 @@ uuid = "1a1011a3-84de-559e-8e89-a11a2f7dc383"
[[Sockets]]
uuid = "6462fe0b-24de-5631-8697-dd941f90decc"
+[[SoftGlobalScope]]
+deps = ["Test"]
+git-tree-sha1 = "012661b70364840fcd380912d878d96f7bf95ff3"
+uuid = "b85f4697-e234-5449-a836-ec8e2f98b302"
+version = "1.0.10"
+
[[SparseArrays]]
deps = ["LinearAlgebra", "Random"]
uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
@@ -121,17 +133,25 @@ uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
deps = ["LinearAlgebra", "SparseArrays"]
uuid = "10745b16-79ce-11e8-11f9-7d13ad32a3b2"
-[[TOML]]
-deps = ["Dates"]
-uuid = "9d418dce-91a8-11e8-0173-7b01a971d501"
-
[[Test]]
deps = ["Distributed", "InteractiveUtils", "Logging", "Random"]
uuid = "8dfed614-e22c-5e08-85e1-65c5234f0b40"
[[UUIDs]]
-deps = ["Random"]
+deps = ["Random", "SHA"]
uuid = "cf7118a7-6976-5b1a-9a39-7adc72f591a4"
[[Unicode]]
uuid = "4ec0a83e-493e-50e2-b9ac-8f72acf5a8f5"
+
+[[VersionParsing]]
+deps = ["Compat"]
+git-tree-sha1 = "c9d5aa108588b978bd859554660c8a5c4f2f7669"
+uuid = "81def892-9a0e-5fdd-b105-ffc91e053289"
+version = "1.1.3"
+
+[[ZMQ]]
+deps = ["BinaryProvider", "FileWatching", "Libdl", "Sockets", "Test"]
+git-tree-sha1 = "34e7ac2d1d59d19d0e86bde99f1f02262bfa1613"
+uuid = "c2297ded-f4af-51ae-bb23-16f91089e4e1"
+version = "1.0.0"
diff --git a/Project.toml b/Project.toml
index ebae8eb..116ec28 100644
--- a/Project.toml
+++ b/Project.toml
@@ -3,7 +3,9 @@ uuid = "a2de2ff4-d7bb-11e8-2879-f9ef9fa2c94f"
version = "0.1.0"
[deps]
-JuliaAcademyData = "18b7da76-0988-5e3b-acac-6290be3a708f"
+Glob = "c27321d9-0574-5035-807b-f59d2c89b15c"
+IJulia = "7073ff75-c697-5162-941a-fcdaad2a7d2a"
+JSON = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
Literate = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
Pkg = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
+#
+# But let's examine that line-fitting first as its simplicity makes a number of
+# points clear. To begin, let's load some data.
+
+using DifferentialEquations, CSV #src
+import Random #src
+Random.seed!(20) #src
+generate_data(ts) = solve(ODEProblem([1.0,1.0],(0.0,10.0),[1.5,1.0,3.0,1.0]) do du,u,p,t; du[1] = p[1]*u[1] - p[2]*prod(u); du[2] = -p[3]*u[2] + p[4]*prod(u); end, saveat=ts)[1,:].*(1.0.+0.02.*randn.()).+0.05.*randn.() #src
+ts = 0:.005:1 #src
+ys = generate_data(ts) #src
+CSV.write(datapath("data/020-descent-data.csv"), (t=ts, y=ys)) #src
+
+using CSV
+df = CSV.read(datapath("data/020-descent-data.csv"))
+#-
+using Plots
+scatter(df.t, df.y, xlabel="time", label="data")
+
+# Now we want to fit some model to this data — for a linear model we just need
+# two parameters:
+#
+# $$
+# y = m x + b
+# $$
+#
+# Lets create a structure that represents this:
+
+mutable struct LinearModel
+ m::Float64
+ b::Float64
+end
+(model::LinearModel)(x) = model.m*x + model.b
+
+# And create a randomly picked model to see how we do:
+linear = LinearModel(randn(), randn())
+plot!(df.t, linear.(df.t), label="model")
+
+# Of course, we just chose our `m` and `b` at random here, of course it's not
+# going to fit our data well! Let's quantify how far we are from an ideal line
+# with a _loss_ function:
+
+loss(f, xs, ys) = sum((f.(xs) .- ys).^2)
+loss(linear, df.t, df.y)
+
+# That's a pretty big number — and we want to decrease it. Let's update our plot
+# to include this loss value in the legend so we can keep track:
+
+p = scatter(df.t, df.y, xlabel="time", label="data")
+plot!(p, df.t, linear.(df.t), label="model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# And now we want to try to improve the fit. To do so, we just need to make
+# the loss function as small as possible. We can of course simply try a bunch
+# of values and brute-force a "good" solution. Plotting this as a three-dimensional
+# surface gives us the imagery of a hill, and our goal is to find our way to the bottom:
+
+ms, bs = (-1:.01:6, -2:.05:2.5)
+surface(ms, bs, [loss(LinearModel(m, b), df.t, df.y) for b in bs for m in ms], xlabel="m values", ylabel="b values", title="loss value")
+
+# A countour plot makes it a bit more obvious where the minimum is:
+
+contour(ms, bs, [loss(LinearModel(m, b), df.t, df.y) for b in bs for m in ms], levels=150, xlabel="m values", ylabel="b values")
+
+# But building those graphs are expensive! And it becomes completely intractible as soon as we
+# have more than a few parameters to fit. We can instead just try nudging the
+# current model's values to simply figure out which direction is "downhill":
+
+linear.m += 0.1
+plot!(p, df.t, linear.(df.t), label="new model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# We'll either have made things better or worse — but either way it's easy to
+# see which way to change `m` in order to improve our model.
+#
+# Essentially, what we're doing here is we're finding the derivative of our
+# loss function with respect to `m`, but again, there's a bit to be desired
+# here. Instead of evaluating the loss function twice and observing the difference,
+# we can just ask Julia for the derivative! This is the heart of differentiable
+# programming — the ability to ask a _complete program_ for its derivative.
+#
+# There are several techniques that you can use to compute the derivative. We'll
+# use the [Zygote package](https://fluxml.ai/Zygote.jl/latest/) first. It will
+# take a second as it compiles the "adjoint" code to compute the derivatives.
+# Since we're doing this in multiple dimensions, the two derivatives together
+# are called the gradient:
+
+using Zygote
+grads = Zygote.gradient(linear) do m
+ return loss(m, df.t, df.y)
+end
+grads
+
+# So there we go! Zygote saw that the model was gave it — `linear` — had two fields and thus
+# it computed the derivative of the loss function with respect to those two
+# parameters.
+#
+# Now we know the slope of our loss function — and thus
+# we know which way to move each parameter to improve it! We just need to iteratively walk
+# downhill! We don't want to take too large a step, so we'll multiply each
+# derivative by a "learning rate," typically called `η`.
+η = 0.001
+linear.m -= η*grads[1][].m
+linear.b -= η*grads[1][].b
+
+plot!(p, df.t, linear.(df.t), label="updated model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# Now we just need to do this a bunch of times!
+
+for i in 1:200
+ grads = Zygote.gradient(linear) do m
+ return loss(m, df.t, df.y)
+ end
+ linear.m -= η*grads[1][].m
+ linear.b -= η*grads[1][].b
+ i > 40 && i % 10 != 1 && continue
+#nb IJulia.clear_output(true)
+ scatter(df.t, df.y, label="data", xlabel="time", legend=:topleft)
+ display(plot!(df.t, linear.(df.t), label="model (loss: $(round(loss(linear, df.t, df.y), digits=3)))"))
+end
+
+#src === CREATING GIF ===
+f = let #src
+ linear = LinearModel(randn(), randn()) #src
+ f = @gif for i in 1:150 #src
+ grads = Zygote.gradient(linear) do m #src
+ return loss(m, df.t, df.y) #src
+ end #src
+ linear.m -= η*grads[1][].m #src
+ linear.b -= η*grads[1][].b #src
+ scatter(df.t, df.y, label="data", xlabel="time", legend=:topleft) #src
+ plot!(df.t, linear.(df.t), label="model (loss: $(round(loss(linear, df.t, df.y), digits=3)))") #src
+ end #src
+ mv(f.filename, datapath("images/020-linear.gif")) #src
+end #src
+
+
+
+# That's looking pretty good now! You might be saying this is crazy — I know
+# how to do a least squares fit! And you'd be right — in this case you can
+# easily do this with a linear solve of the system of equations:
+m, b = [df.t ones(size(df.t))] \ df.y
+
+@show (m, b)
+@show (linear.m, linear.b);
+
+# ## Exercise: Use gradient descent to fit a quadratic model to the data
+#
+# Obviously a linear fit leaves a bit to be desired here. Try to use the same
+# framework to fit a quadratic model. Check your answer against the algebraic
+# solution with the `\` operator.
+
+struct PolyModel
+ p::Vector{Float64}
+end
+function (m::PolyModel)(x)
+ r = m.p[1]*x^0
+ for i in 2:length(m.p)
+ r += m.p[i]*x^(i-1)
+ end
+ return r
+end
+poly = PolyModel(rand(3))
+loss(poly, df.t, df.y)
+η = 0.001
+for i in 1:1000
+ grads = Zygote.gradient(poly) do m
+ return loss(m, df.t, df.y)
+ end
+ poly.p .-= η.*grads[1].p
+end
+scatter(df.t, df.y, label="data", legend=:topleft)
+plot!(df.t, poly.(df.t), label="model by descent")
+plot!(df.t, PolyModel([df.t.^0 df.t df.t.^2] \ df.y).(df.t), label="model by linear solve")
+
+# ## Nonlinearities
+#
+# Let's see what happens when load a bit more data:
+
+let #src
+ ts = 0:.04:8 #src
+ ys = generate_data(ts) #src
+ CSV.write(datapath("data/020-descent-data-2.csv"), (t=ts, y=ys)) #src
+end #src
+df2 = CSV.read(datapath("data/020-descent-data-2.csv"))
+scatter(df2.t, df2.y, xlabel="t", label="more data")
+
+# Now what? This clearly won't be fit well with a low-order polynomial, and
+# even a high-order polynomial will get things wrong once we try to see what
+# will happen in the "future"!
+#
+# Let's use a bit of knowledge about where this data comes from: these happen
+# to be the number of rabbits in a predator-prey system! We can express the
+# general behavior with a pair of differential equations:
+#
+# $$
+# x' = \alpha x - \beta x y \\
+# y' = -\delta y + \gamma x y
+# $$
+#
+# * $x$ is the number of rabbits (🐰)
+# * $y$ is the number of wolves (🐺)
+# * $\alpha$ and $\beta$ describe the growth and death rates for the rabbits
+# * $\gamma$ and $\delta$ describe the growth and death rates for the wolves
+#
+# But we don't know what those rate constants are — all we have is the population
+# of rabbits over time.
+#
+# These are the classic Lotka-Volterra equations, and can be expressed in Julia
+# using the [DifferentialEquations](https://github.com/JuliaDiffEq/DifferentialEquations.jl) package:
+using DifferentialEquations
+function rabbit_wolf(du,u,p,t)
+ 🐰, 🐺 = u
+ α, β, δ, γ = p
+ du[1] = α*🐰 - β*🐰*🐺
+ du[2] = -δ*🐺 + γ*🐰*🐺
+end
+u0 = [1.0,1.0]
+tspan = extrema(df2.t)
+p = rand(4).+1 # We don't know what this is!
+## But lets see what the model looks like right now:
+prob = ODEProblem(rabbit_wolf,u0,tspan,p)
+sol = solve(prob, Tsit5(), saveat=df2.t)
+
+scatter(df2.t, df2.y, xlabel="t", label="more data")
+plot!(sol, label=["rabbits","wolves"])
+
+# So we're going to have to improve this — unlike the previous examples, we don't
+# have an easy algebraic solution here! But let's try using gradient descent.
+# The easiest way to get gradients out of a differential equation solver right
+# now is through the [DiffEqFlux package](https://github.com/JuliaDiffEq/DiffEqFlux.jl), and instead of manually converging,
+# we can use the Flux package to automatically (and more smartly) handle the gradient descent. Just
+# like before, though, we compute the loss of the model evaluation — and in this
+# case the model is _solving a differential equation!_
+using Flux, DiffEqFlux
+p = Flux.param(ones(4))
+diffeq_loss(p, xs, ys) = sum(abs2, diffeq_rd(p,prob,Tsit5(),saveat=df2.t)[1,:] .- df2.y)
+
+# This works slightly differently — we now track the gradients directly in the
+# p vector:
+p.grad
+#-
+l = diffeq_loss(p, df2.t, df2.y)
+#-
+DiffEqFlux.Tracker.back!(l) # we need to back-propagate our tracking of the gradients
+p.grad # but now we can see the gradients involved in that computation!
+
+# So now we can do exactly the same thing as before: iteratively update the parameters
+# to descend to a (hopefully) well-fit model:
+#
+# ```julia
+# p.data .-= η*p.grad
+# ```
+#
+# But we can be a bit smarter about this just by asking Flux to handle everything
+# with its train! function and associated functionality:
+
+data = Iterators.repeated((df2.t, df2.y), 150)
+opt = ADAM(0.1)
+history = Any[] #src
+cb = function () #callback function to observe training
+#nb IJulia.clear_output(true)
+ plt = scatter(df2.t, df2.y, label="data", ylabel="population (thousands)", xlabel="t")
+ display(plot!(plt, solve(remake(prob,p=Flux.data(p)),Tsit5(),saveat=0.1),
+ ylim=(0,8), label=["rabbits","wolves"], title="loss: $(round(Flux.data(diffeq_loss(p, df2.t, df2.y)), digits=3))"))
+ push!(history, plt) #src
+end
+Flux.train!((xs, ys)->diffeq_loss(p, xs, ys), [p], data, opt, cb = cb)
+
+f = @gif for i in 1:length(history) #src
+ plot(history[i]) #src
+end #src
+mv(f.filename, datapath("images/020-diffeq.gif")) #src
+
+# # Summary
+#
+# You can now see the power of differentiating whole programs — we can easily
+# and efficiently tune parameters without brute forcing solutions. Gradient
+# descent easily extends to machine learning and artificial intelligence
+# applications — and there are a number of tricks that can increase its efficiency
+# and help avoid local minima. There are a variety of other places where knowing the gradient can
+# be powerful and helpful.
diff --git a/Courses/Differentiable Programming/030 Neural Differential Equations.jl b/Courses/Differentiable Programming/030 Neural Differential Equations.jl
new file mode 100644
index 0000000..0b0f013
--- /dev/null
+++ b/Courses/Differentiable Programming/030 Neural Differential Equations.jl
@@ -0,0 +1,86 @@
+using Flux, DiffEqFlux, StochasticDiffEq, Plots, DiffEqMonteCarlo
+
+u0 = Float32[2.; 0.]
+datasize = 30
+tspan = (0.0f0,1.0f0)
+
+function trueODEfunc(du,u,p,t)
+ true_A = [-0.1 2.0; -2.0 -0.1]
+ du .= ((u.^3)'true_A)'
+end
+t = range(tspan[1],tspan[2],length=datasize)
+mp = Float32[0.2,0.2]
+function true_noise_func(du,u,p,t)
+ du .= mp.*u
+end
+prob = SDEProblem(trueODEfunc,true_noise_func,u0,tspan)
+
+# Take a typical sample from the mean
+monte_prob = MonteCarloProblem(prob)
+monte_sol = solve(monte_prob,SOSRI(),num_monte = 100)
+monte_sum = MonteCarloSummary(monte_sol)
+sde_data = Array(timeseries_point_mean(monte_sol,t))
+
+dudt = Chain(x -> x.^3,
+ Dense(2,50,tanh),
+ Dense(50,2))
+ps = Flux.params(dudt)
+n_sde = x->neural_dmsde(dudt,x,mp,tspan,SOSRI(),saveat=t,reltol=1e-1,abstol=1e-1)
+
+pred = n_sde(u0) # Get the prediction using the correct initial condition
+
+dudt_(u,p,t) = Flux.data(dudt(u))
+g(u,p,t) = mp.*u
+nprob = SDEProblem(dudt_,g,u0,(0.0f0,1.2f0),nothing)
+
+monte_nprob = MonteCarloProblem(nprob)
+monte_nsol = solve(monte_nprob,SOSRI(),num_monte = 100)
+monte_nsum = MonteCarloSummary(monte_nsol)
+#plot(monte_nsol,color=1,alpha=0.3)
+p1 = plot(monte_nsum, title = "Neural SDE: Before Training")
+scatter!(p1,t,sde_data',lw=3)
+
+scatter(t,sde_data[1,:],label="data")
+scatter!(t,Flux.data(pred[1,:]),label="prediction")
+
+function predict_n_sde()
+ n_sde(u0)
+end
+loss_n_sde1() = sum(abs2,sde_data .- predict_n_sde())
+loss_n_sde10() = sum([sum(abs2,sde_data .- predict_n_sde()) for i in 1:10])
+Flux.back!(loss_n_sde1())
+
+data = Iterators.repeated((), 10)
+opt = ADAM(0.025)
+cb = function () #callback function to observe training
+ sample = predict_n_sde()
+ # loss against current data
+ display(sum(abs2,sde_data .- sample))
+ # plot current prediction against data
+ cur_pred = Flux.data(sample)
+ pl = scatter(t,sde_data[1,:],label="data")
+ scatter!(pl,t,cur_pred[1,:],label="prediction")
+ display(plot(pl))
+end
+
+# Display the SDE with the initial parameter values.
+cb()
+
+Flux.train!(loss_n_sde1 , ps, Iterators.repeated((), 100), opt, cb = cb)
+Flux.train!(loss_n_sde10, ps, Iterators.repeated((), 20), opt, cb = cb)
+
+dudt_(u,p,t) = Flux.data(dudt(u))
+g(u,p,t) = mp.*u
+nprob = SDEProblem(dudt_,g,u0,(0.0f0,1.2f0),nothing)
+
+monte_nprob = MonteCarloProblem(nprob)
+monte_nsol = solve(monte_nprob,SOSRI(),num_monte = 100)
+monte_nsum = MonteCarloSummary(monte_nsol)
+#plot(monte_nsol,color=1,alpha=0.3)
+p2 = plot(monte_nsum, title = "Neural SDE: After Training", xlabel="Time")
+scatter!(p2,t,sde_data',lw=3,label=["x" "y" "z" "y"])
+
+plot(p1,p2,layout=(2,1))
+
+savefig("neural_sde.pdf")
+savefig("neural_sde.png")
diff --git a/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl b/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl
new file mode 100644
index 0000000..6cc7a7f
--- /dev/null
+++ b/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl
@@ -0,0 +1,260 @@
+# # How To Aim Your Flagon
+
+#-
+
+# ## Loading your Trebuchet
+
+#-
+
+# Today we practice the ancient medieval art of throwing stuff. First up, we load our trebuchet simulator, Trebuchet.jl.
+
+using Trebuchet
+
+# We can see what the trebuchet looks like, by explicitly creating a trebuchet state, running a simulation, and visualising the trajectory.
+
+t = TrebuchetState()
+simulate(t)
+visualise(t)
+
+# For training and optimisation, we don't need the whole visualisation, just a simple function that accepts and produces numbers. The `shoot` function just takes a wind speed, angle of release and counterweight mass, and tells us how far the projectile got.
+
+function shoot((wind, angle, weight))
+ Trebuchet.shoot((wind, Trebuchet.deg2rad(angle), weight))[2]
+end
+
+#-
+
+shoot([0, 45, 400])
+
+# It's worth playing with these parameters to see the impact they have. How far can you throw the projectile, tweaking only the angle of release?
+
+shoot([0, 40, 400])
+
+#-
+
+# There's actually a much better way of aiming the trebuchet. Let's load up a machine learning library, Flux, and see what we can do.
+
+using Flux, Trebuchet
+using Flux.Tracker: gradient, forwarddiff
+
+# Firstly, we're going to wrap `shoot` to take a _parameter vector_ (just a list of the three numbers we're interested in). There's also a call to `forwarddiff` here, which tells Flux to differentiate the trebuchet itself using forward mode. The number of parameters is small, so forward mode will be the most efficient way to do it. Otherwise Flux defaults to reverse mode.
+
+shoot(ps) = forwarddiff(p->shoot(p...), ps)
+
+# We can get a distance as usual.
+
+shoot([0, 45, 200])
+
+# But we can also get something much more interesting: *gradients* for each of those parameters with respect to distance.
+
+gradient(x->forwarddiff(shoot, x), [0.0, 45, 200])
+
+# What does these numbers mean? The gradient tells us, very roughly, that if we increase a parameter – let's say we make wind speed 1 m/s stronger – distance will also increase by about 4 metres. Let's try that.
+Zygote.gradient(x->forwarddiff(shoot, x), [0.0, 45, 200])
+
+shoot([1, 45, 200])
+
+# Lo and behold, this is indeed about four metres further!
+
+shoot([1, 45, 200]) - shoot([0, 45, 200])
+
+# So this seems like very useful information if we're trying to aim, or maximise distance. Notice that our gradient for the release angle is negative – increasing angle will decrease distance, so in other words we should probably *decrease* angle if we want more distance. Let's try that.
+
+shoot([0, 10, 200])
+
+# Oh no, this is actually *less* far than before!
+
+#-
+
+# So if the angle is too shallow, the projectile doesn't spend enough time in the air to gain any distance before hitting the ground. But if it's too high, the projectile doesn't have enough horizontal speed even with lots of time in the air. So we'll have to find a middle ground.
+#
+# More generally, the lesson here is that the gradient only gives you limited information; it helps us take a small step towards a better aim, and we can keep iterating to get to the best possible aim. For example, we choose a starting angle:
+
+angle = 45
+shoot([0, angle, 200])
+
+# Get a gradient for `angle` alone:
+
+dangle = gradient(angle -> shoot(Tracker.collect([0, angle, 200])), angle)[1] |> Flux.data
+
+# Update the angle, using the learning rate η:
+
+η = 10
+angle += η*dangle
+
+#-
+
+shoot([0, angle, 200])
+
+# Now we just lather, rinse and repeat! Ok, maybe we should write a loop to automate this a bit.
+
+for i = 1:10
+ dangle = gradient(angle -> shoot(Tracker.collect([0, angle, 200])), angle)[1] |> Flux.data
+ angle += η*dangle
+ @show angle
+end
+shoot([0, angle, 200])
+
+# Notice how the change in the angle slows down as things converge. Turns out the best angle is about 30 degrees, and we can hit about 90 metres.
+#
+# We can make this nicely repeatable and get the best angle for any given wind speed.
+
+function best_angle(wind)
+ angle = 45
+ objective(angle) = shoot(Tracker.collect([wind, angle, 200]))
+ for i = 1:10
+ dangle = gradient(objective, angle)[1] |> Flux.data
+ angle += η*dangle
+ end
+ return angle
+end
+
+#-
+
+best_angle(0)
+
+#-
+
+best_angle(10)
+
+#-
+
+best_angle(-10)
+
+# It turns out that if the wind is on our side, we should just throw the projectile upwards and let it get blown along. If the wind is strong against us, just chuck that stone right into it.
+
+t = TrebuchetState(release_angle = deg2rad(19), wind_speed = -10)
+simulate(t)
+visualise(t)
+
+# ## Accuracy Matters
+
+#-
+
+# In optimisation terms, we just created an objective (distance) and tried to maximise that objective. Flinging boulders as far as possible has its moments, but lacks a certain subtlety. What if we instead want to hit a precise target?
+
+t = TrebuchetState()
+simulate(t)
+visualise(t, 50)
+
+# The way to do this is to state the problem in terms of maximising, or minisming, some number – the objective. In this case, an easy way to come up with an objective is to take the difference from our target (gets closer to 0 as aim gets better) and square it (so it's always positive: 0 is the lowest *and* best possible score).
+
+#-
+
+# Here's a modified `best_angle` function that takes a target and tells us the distance it acheived.
+
+η = 0.1
+function best_angle(wind, target)
+ angle = 45
+ objective(angle) = (shoot(Tracker.collect([wind, angle, 200])) - target)^2
+ for i = 1:30
+ dangle = gradient(objective, angle)[1] |> Flux.data
+ angle -= η*dangle
+ end
+ return angle, shoot([wind, angle, 200])
+end
+
+# It's pretty accurate!
+
+best_angle(0, 50)
+
+# Even when we try to push it, by making wind really strong.
+
+best_angle(-20, 35)
+
+#-
+
+t = TrebuchetState(release_angle = deg2rad(21.8), weight = 200, wind_speed = -20)
+simulate(t)
+visualise(t, 35)
+
+# ## Siege Weapon Autopilot
+
+#-
+
+# Finally, we go one level more meta by training a neural network to aim the trebuchet for us. Rather than solving a whole optimisation problem every time we want to aim, we can just ask the network for good parameters and get them in constant time.
+#
+# Here's a simple multi layer perceptron. Its input is two parameters (wind speed and target) and its output is two more (release angle and counterweight mass).
+
+model = Chain(Dense(2, 16, σ),
+ Dense(16, 64, σ),
+ Dense(64, 16, σ),
+ Dense(16, 2)) |> f64
+
+θ = params(model)
+
+function aim(wind, target)
+ angle, weight = model([wind, target])
+ angle = σ(angle)*90
+ weight = weight + 200
+ angle, weight
+end
+
+distance(wind, target) = shoot(Tracker.collect([wind, aim(wind, target)...]))
+
+# The model's initial guesses will be fairly random, and miss the mark.
+
+aim(0, 70)
+
+#-
+
+distance(0, 70)
+
+# However, just as before, we can define an objective – or loss – and get gradients.
+
+function loss(wind, target)
+ try
+ (distance(wind, target) - target)^2
+ catch e
+ # Roots.jl sometimes give convergence errors, ignore them
+ param(0)
+ end
+end
+
+loss(0, 70)
+
+# This time, though, we'll get gradients for the *model parameters*, and updating these will improve the network's accuracy. This works because we're able to differentiate the *whole program*; the backwards pass propagates errors through the trebuchet simulator and then through the ML model.
+
+dθ = gradient(θ) do
+ loss(0, 70)
+end
+dθ[model[1].W]
+
+#-
+
+DIST = (20, 100) # Maximum target distance
+SPEED = 5 # Maximum wind speed
+
+lerp(x, lo, hi) = x*(hi-lo)+lo
+
+randtarget() = (randn() * SPEED, lerp(rand(), DIST...))
+
+#-
+
+using Statistics
+
+meanloss() = mean(sqrt(loss(randtarget()...)) for i = 1:100)
+
+opt = ADAM()
+
+dataset = (randtarget() for i = 1:10_000)
+
+Flux.train!(loss, θ, dataset, opt, cb = Flux.throttle(() -> @show(meanloss()), 10))
+
+# After only a few minutes of training, we're getting solid accuracy, even on hard wind speeds and targets. You can run the training loop again to improve the accuracy even further.
+
+wind, target = -10, 50
+angle, mass = Flux.data.(aim(wind, target))
+t = TrebuchetState(release_angle = deg2rad(angle), weight = mass, wind_speed = wind)
+simulate(t)
+visualise(t, target)
+
+# Notice that aiming with a neural net in one shot is significantly faster than solving the optimisation problem; and we only have a small loss in accuracy.
+
+@time aim(wind, target)
+
+#-
+
+@time best_angle(wind, target)
+
+#-
diff --git a/Courses/Differentiable Programming/050 Forward Differentiation.jl b/Courses/Differentiable Programming/050 Forward Differentiation.jl
new file mode 100644
index 0000000..fdc0453
--- /dev/null
+++ b/Courses/Differentiable Programming/050 Forward Differentiation.jl
@@ -0,0 +1,325 @@
+module ADPackages #src
+# Some settings for running this interactively #src
+interactive_use = false #src
+plotting_off = false #src
+using BenchmarkTools #src
+if interactive_use #src
+BenchmarkTools.DEFAULT_PARAMETERS.seconds = 0.1 #src
+end #src
+
+# # Using AD packages
+#
+# While a theoretical understanding behind how automatic differentiation work
+# is interesting, in practice, being able to use existing AD packages might
+# be good enough so this is where we will start.
+# Julia has many excellent packages for AD. The purpose of this lecture
+# for you to try a few of them out and apply them to real problems like solving
+# optimization problems using AD.
+
+# ## ForwardDiff
+#
+# The most popular package for AD in Julia is [`ForwardDiff`](https://github.com/JuliaDiff/ForwardDiff.jl).
+# It uses something called *forward mode automatic differentiation* using "Dual numbers"
+# and operator overloading. Forward mode AD is efficient if the function
+# being differentiated is $\mathbb{R}^N -> \mathbb{R}^M$ with $N <= M$. In other words,
+# the dimension of the input argument should be equal or greater than the number of
+# output arguments.
+# Foroward mode AD is however not so efficient for example when `M = 1` and `N` is big, which is common in
+# e.g. machine learning. In these cases *reverse mode automatic differentiation* is
+# more efficient, and we will look at that later.
+
+# ### Derivative of scalar functions
+#
+# To have a function to start experimenting with, we define the (scalar to
+# scalar) function `f(x)` and its analytical derivative
+# `fp(x)`
+
+f(x) = exp(x) / (sin(x)^3 + cos(x)^3);
+fp(x) = exp(x) * (3sin(x) + sin(3x) + 2cos(3x)) / 2(sin(x)^3 + cos(x)^3)^2;
+
+# We can visualize the function and the derivative (here using the Plots.jl package)
+if !plotting_off #src
+using Plots
+end #src
+xs = 0.0:0.01:1.4
+if !plotting_off #src
+plot(xs, [f.(xs), fp.(xs)]; labels = ["f" "fp"])
+end #src
+
+# The only thing to do to differentiate this function using AD is to import `ForwardDiff`
+# and call the `ForwardDiff.derivative` function with the function we want to differentiate and
+# at what point we want the derivative. The function should take a scalar as an argument
+# and return a scalar and that is what our function `f` above does.
+
+import ForwardDiff
+ad_derivative = ForwardDiff.derivative(f, pi/4)
+analytical_derivative = fp(pi/4)
+@assert ad_derivative ≈ analytical_derivative #src
+@show ad_derivative - analytical_derivative;
+
+# We can see that the AD derivative is "exact" (at least exact in the sense of floating
+# point precision) to the analytical ones.
+
+# #### Performance
+#
+# It can be interesting to see what the performance of using AD vs the the performance of the
+# analytical derivative. We can use the benchmark framework [`BenchmarkTools.jl`](https://github.com/JuliaCI/BenchmarkTools.jl)
+# to help us make accurate benchmarks even for functions that execute very quickly.
+
+using BenchmarkTools
+
+@assert VERSION < v"1.1" "revise benchmarking for 1.1" #src
+
+############################################################ #src
+# TODO: THIS IS ONLY TRUE ON MASTER, THE OPTIMIZATION DOES NOT HAPPEN ON JULIA 1.0.1 #src
+# If we do some napkin math, we can see that the reported time here is completely bogus! #src
+# Making the not too terrible assumption that a CPU can do one operation per clockcycle and that #src
+# the CPU you are using has approximately 3 GHz then one instruction should take ~0.3 ns which is #src
+# much longer than the reported time here. And computing this derivative need to compute `sin`, `cos` #src
+# etc which take many CPU instructions. #src
+# We have now encounted one of hard problems when benchmarking, to make sure that the computer is actually #src
+# computing the things you want it to. What happens here is that the Julia compiler is able #src
+# to figure out that the input we gave the function (`pi/4`) is a constant and the optimizer #src
+# then figures out the result during compile time. We can see this as follows: #src
+# #src
+#g() = ForwardDiff.derivative(f, pi/4) #src
+# #src
+## Looking at the generated code for #src
+# #src
+#@code_llvm g() #src
+# #src
+# We can see that the function has been optimized to just return a single value. #src
+# The exact value looks a bit odd because it is written #src
+# but reinterpreting it as a Float64 value we can see that it is just the same #src
+# derivative as was returned from ForwardDiff: #src
+# #src
+#@show reinterpret(Float64, 0x4008D06AE62ADC94) #src
+# #src
+#@show ForwardDiff.derivative(f, pi/4) #src
+# #src
+# One way we can trick the optimizer (at least with the current version of it) to not optimized #src
+# away the computation #src
+# is to encapsulate our value in a container like a [`Ref`](https://docs.julialang.org/en/v1/base/c/#Core.Ref) #src
+# #src
+##################################################################################### #src
+
+# A function can be benchmarked by prepending the call with `@btime`.
+# This will run the function multiple time and collect statistics on the
+# time it took to execute the function:
+
+println("Original function")
+@btime f(pi/4);
+println("AD derivative")
+@btime ForwardDiff.derivative(f, pi/4);
+println("Analytical derivative")
+@btime fp(pi/4);
+
+# We can here see that for the way we implemented the analytical derivative there is virtually no
+# performance difference between the AD version and the analyitical version.
+# However, it should be noted that the current version of the analytical function is not the
+# one with the best performance. Feel free to try to improve it.
+
+# A nice thing about AD is that you don't have to spend time making sure that
+# not only is the derivative correct, but that it is also efficiently computed.
+# By using AD, you get "free" performance for the derivative by optimizing the function itself.
+
+# #### Second derivatives
+#
+# For scalar functions `ForwardDiff` does not come with built in functionality for computing
+# the second derivative. It is, fortunately, very easy to create such a function ourselves.
+# The second derivative is just the derivative of the derivative which we can implement as:
+
+derivative2(f, x) = ForwardDiff.derivative(z -> ForwardDiff.derivative(f, z), x)
+
+@assert derivative2(f, pi/4) ≈ -6.203532787672101 #src
+@show derivative2(f, pi/4);
+
+# Here, we created an anonymous function that computes derivatives of `f`,
+# `z -> ForwardDiff.derivative(f, z)`, and then we used that as the input
+# derivative for another `ForwardDiff.derivative` call. The derivative
+# of the derivative gives the second derivative. Simple!
+# Feel free to compute the second derivative by hand and verify that the result
+# is correct (and appreciate that AD savees you from doing it in the first place).
+# The correct analytical result is `-2sqrt(2) * exp(pi/4)`.
+
+# #### Differentiating functions with parameters
+#
+# It is common to have a function that depends on some parameters that are considered
+# fixed in the context of differentiation.
+# An example of this might be the function `g` (and its derivative `gp) below:
+
+g(x, a) = (x - a)^3
+gp(x, a) = 3*(x - a)^2
+
+# Here, `g` has the parameter `a` and we want to take the derivative with respect to `x`.
+# Recall that `ForwardDiff.derivative` needs a function that takes only one
+# argument, but `g` above takes two arguments, so it clearly cannot be used directly.
+# The solution is to create what is typically called a "closure", which is a new function
+# that "closes" over some parameter space.
+# For example, consider:
+
+const a = 3
+g2(x) = g(x, a)
+
+@show (2 - a)^3
+@show g2(2);
+
+# We now have a new function `g2` which takes only one argument (`x`) and "closes" over the
+# variable `a`. We can now differentiate `g2`.
+
+@show ForwardDiff.derivative(g2, 2.0)
+@show gp(2.0, 3);
+
+# It is possible to write this a bit more succintly using an anonymous function
+
+ForwardDiff.derivative(x -> g(x, a), 2.0)
+
+# ## Gradients
+#
+# If our function takes a vector as input and returns a scalar, the derivative
+# is a vector (called a gradient) which gives the sensitivity of the output with respect to
+# all inputs. A quite common function to use in examples involving optimization
+# is the [Rosenbrock function](https://en.wikipedia.org/wiki/Rosenbrock_function), defined as:
+
+function rosenbrock(x)
+ a = one(eltype(x))
+ b = 100 * a
+ result = zero(eltype(x))
+ for i in 1:length(x)-1
+ result += (a - x[i])^2 + b*(x[i+1] - x[i]^2)^2
+ end
+ return result
+end
+
+# Evaluating `rosenbrock` with a vector input indeed gives a scalar back.
+
+rosenbrock([1.0, 0.5, 2.0])
+@assert rosenbrock([1.0, 0.5, 2.0]) == 331.5 #src
+
+# We can see how this function looks by plotting it
+
+xs = -3:0.1:3
+ys = -3:0.1:3
+zs = [rosenbrock([x, y]) for x in xs, y in ys]
+if !plotting_off #src
+contour(xs, ys, zs; levels=40)
+end #src
+
+# Evaluating the `gradient` is almost as simple as the `derivative`:
+
+x_vec = [1.0, 2.0]
+ForwardDiff.gradient(rosenbrock, x_vec)
+
+# ### Performance
+#
+# When evaluating the gradient we are dealing with `Vector`s which require allocation
+# so there are a few extra performance considerations for `gradient` compared to `derivative`
+
+# #### Preallocating output
+#
+# `ForwardDiff.gradient` returns a `Vector` which needs to be allocated. We can preallocate
+# this so `ForwardDiff` doesn't need to to it by itself.
+
+z_vec = similar(x_vec)
+ForwardDiff.gradient!(z_vec, rosenbrock, x_vec)
+@show z_vec;
+
+# The result was now stored in the, by us, allocated `z_vec`. We can check the performance difference
+
+println("No preallocation")
+@btime ForwardDiff.gradient(rosenbrock, $x_vec)
+println("No preallocation")
+@btime ForwardDiff.gradient!($z_vec,rosenbrock, $x_vec)
+
+# We can see that we do one allocation less and that performance is significantly
+# improved.
+
+# #### Preallocating internal datastructures
+#
+# Even though we preallocated the output vector there are some
+# internal data structures used by ForwardDiff that we in addition can preallocate
+# This is done by creating a `GradientConfig`:
+
+gradient_cache = ForwardDiff.GradientConfig(rosenbrock, x_vec)
+@btime ForwardDiff.gradient!($z_vec, rosenbrock, $x_vec, $gradient_cache);
+
+# Which as we can see further increase performance.
+# All of this is documented in the ForwardDiff manual so the takehome message is
+# to read the manual of the package one uses. There are often valuable information
+# there that could (like in this case) significantly improve performance.
+
+# ### Solving optimization using ForwardDiff
+#
+# [`Optim`](https://github.com/JuliaNLSolvers/Optim.jl) is a package that has many useful optimization routines.
+# If you can provide the gradient (and even sec) you get access to optimization routines that can
+# have significantly better performance. Lets use first try to just optimize the function without
+# using any gradient information. This will default to using the
+# [Nelder-Mead method](https://en.wikipedia.org/wiki/Nelder%E2%80%93Mead_method).
+# We also stick a `@btime` in there to see how long time the optimization routine take.
+using Random; Random.seed!(1234) #src
+using Optim
+x0 = zeros(10)
+@btime optimize(rosenbrock, x0)
+
+# We can see that we require approximately 620 evaluations of `rosenbrock` before
+# a minimum was found. Let's try giving `Optim` the gradient as well:
+#
+using Random; Random.seed!(1234) #src
+const gradient_cache_optim = ForwardDiff.GradientConfig(rosenbrock, x0)
+const rosenbrock_gradient! = (z, x) -> ForwardDiff.gradient!(z,rosenbrock, x, gradient_cache_optim)
+
+@btime optimize(rosenbrock, rosenbrock_gradient!, x0)
+
+# Now we only called the function 92 times (and in addition the gradient 153 times)
+# Looking at the time taken this was almost a 3x speedup. The minimum we found had a
+# was also significantly smaller than when we used Nelder-Mead
+
+# ## Hessians
+# It is also possible to compute Hessians (second derivative) in a very similar way to `gradient`
+
+ForwardDiff.hessian(rosenbrock, [1.0, 2.0])
+
+# We leave out the details for `ForwardDiff.hessian` here and instead refer to the [`ForwardDiff.hessian`](http://www.juliadiff.org/ForwardDiff.jl/stable/user/api.html#Hessians-of-f(x::AbstractArray)::Real-1)
+# documentation.
+
+# ## Jacobians
+#
+# If our function takes a vector as argument and returns a vector, the derivative is a `Matrix` which
+# is known as the Jacobian. This derivative is useful when we want to solve a nonlinear system of
+# equations.
+# Let's consider the following function that slightly resembles the `rosenbrock` function:
+
+function rosenbrock_vector(x)
+ return [
+ 1 - x[1],
+ 10(x[2]-x[1]^2)
+ ]
+end
+
+# Indeed calling this function with a vector argument returns a vector:
+
+rosenbrock_vector([1.0, 0.5])
+
+# By now, we should be quite familiar with the ForwarDiff interface and you might
+# even guess how we should compute the Jacobian:
+
+ForwardDiff.jacobian(rosenbrock_vector, [1.0, 0.5])
+
+# The Jacobian functionality could be used for example in [`NLsolve.jl`](https://github.com/JuliaNLSolvers/NLsolve.jl),
+# which is a nonlinear equation solver.
+
+# ### Summary `ForwardDiff`
+# This should get you started with using `ForwardDiff`. If your functions do not have too big vectors as
+# input arguments, the performance should be good. It will likely not beat a carefully tuned
+# analytical implementaion of the derivative but it is oftan that from a productivity point of view
+# it is worth using AD.
+
+# ## Revisediff
+#
+# ForwardDiff is using what is known as forward mode differentiation.
+# If the number of input parameters is large and the output is just a scalar
+# then reverse mode differentation is likely more effective.
+#
+# TODO..
+
+end #src
diff --git a/Courses/Differentiable Programming/060 Reverse Differentiation.jl b/Courses/Differentiable Programming/060 Reverse Differentiation.jl
new file mode 100644
index 0000000..e69de29
diff --git a/Courses/Differentiable Programming/Manifest.toml b/Courses/Differentiable Programming/Manifest.toml
new file mode 100644
index 0000000..9b3c023
--- /dev/null
+++ b/Courses/Differentiable Programming/Manifest.toml
@@ -0,0 +1,872 @@
+# This file is machine-generated - editing it directly is not advised
+
+[[AbstractTrees]]
+deps = ["Markdown", "Test"]
+git-tree-sha1 = "6621d9645702c1c4e6970cc6a3eae440c768000b"
+uuid = "1520ce14-60c1-5f80-bbc7-55ef81b5835c"
+version = "0.2.1"
+
+[[Adapt]]
+deps = ["LinearAlgebra", "Test"]
+git-tree-sha1 = "53d8fec4f662088c1202530e338a11a919407f3b"
+uuid = "79e6a3ab-5dfb-504d-930d-738a2a938a0e"
+version = "0.4.2"
+
+[[Arpack]]
+deps = ["BinaryProvider", "Libdl", "LinearAlgebra"]
+git-tree-sha1 = "07a2c077bdd4b6d23a40342a8a108e2ee5e58ab6"
+uuid = "7d9fca2a-8960-54d3-9f78-7d1dccf2cb97"
+version = "0.3.1"
+
+[[ArrayInterface]]
+deps = ["Requires", "Test"]
+git-tree-sha1 = "6a1a371393e56f5e8d5657fe4da4b11aea0bfbae"
+uuid = "4fba245c-0d91-5ea0-9b3e-6abc04ee57a9"
+version = "0.1.1"
+
+[[AssetRegistry]]
+deps = ["Distributed", "JSON", "Pidfile", "SHA", "Test"]
+git-tree-sha1 = "b25e88db7944f98789130d7b503276bc34bc098e"
+uuid = "bf4720bc-e11a-5d0c-854e-bdca1663c893"
+version = "0.1.0"
+
+[[BandedMatrices]]
+deps = ["FillArrays", "LazyArrays", "LinearAlgebra", "MatrixFactorizations", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "dd74592d0952af59b97e12d6f69bfc9cc3a79614"
+uuid = "aae01518-5342-5314-be14-df237901396f"
+version = "0.9.2"
+
+[[Base64]]
+uuid = "2a0f44e3-6c83-55bd-87e4-b1978d98bd5f"
+
+[[BenchmarkTools]]
+deps = ["JSON", "Printf", "Statistics", "Test"]
+git-tree-sha1 = "5d1dd8577643ba9014574cd40d9c028cd5e4b85a"
+uuid = "6e4b80f9-dd63-53aa-95a3-0cdb28fa8baf"
+version = "0.4.2"
+
+[[BinDeps]]
+deps = ["Compat", "Libdl", "SHA", "URIParser"]
+git-tree-sha1 = "12093ca6cdd0ee547c39b1870e0c9c3f154d9ca9"
+uuid = "9e28174c-4ba2-5203-b857-d8d62c4213ee"
+version = "0.8.10"
+
+[[BinaryProvider]]
+deps = ["Libdl", "Logging", "SHA"]
+git-tree-sha1 = "8153fd64131cd00a79544bb23788877741f627bb"
+uuid = "b99e7846-7c00-51b0-8f62-c81ae34c0232"
+version = "0.5.5"
+
+[[BoundaryValueDiffEq]]
+deps = ["BandedMatrices", "DiffEqBase", "DiffEqDiffTools", "ForwardDiff", "LinearAlgebra", "NLsolve", "Reexport", "SparseArrays", "Test"]
+git-tree-sha1 = "0f4a4f86ae63671efd9b41de9dea8ad993f2daad"
+uuid = "764a87c0-6b3e-53db-9096-fe964310641d"
+version = "2.2.3"
+
+[[CSTParser]]
+deps = ["Tokenize"]
+git-tree-sha1 = "376a39f1862000442011390f1edf5e7f4dcc7142"
+uuid = "00ebfdb7-1f24-5e51-bd34-a7502290713f"
+version = "0.6.0"
+
+[[CSV]]
+deps = ["CategoricalArrays", "DataFrames", "Dates", "Mmap", "Parsers", "PooledArrays", "Profile", "Tables", "Unicode", "WeakRefStrings"]
+git-tree-sha1 = "078801ccf5a644df31cef99c9add46107b94aba5"
+uuid = "336ed68f-0bac-5ca0-87d4-7b16caf5d00b"
+version = "0.5.6"
+
+[[Calculus]]
+deps = ["Compat"]
+git-tree-sha1 = "f60954495a7afcee4136f78d1d60350abd37a409"
+uuid = "49dc2e85-a5d0-5ad3-a950-438e2897f1b9"
+version = "0.4.1"
+
+[[CategoricalArrays]]
+deps = ["Compat", "Future", "JSON", "Missings", "Printf", "Reexport"]
+git-tree-sha1 = "26601961df6afacdd16d67c1eec6cfe75e5ae9ab"
+uuid = "324d7699-5711-5eae-9e2f-1d82baa6b597"
+version = "0.5.4"
+
+[[CodecZlib]]
+deps = ["BinaryProvider", "Libdl", "Test", "TranscodingStreams"]
+git-tree-sha1 = "36bbf5374c661054d41410dc53ff752972583b9b"
+uuid = "944b1d66-785c-5afd-91f1-9de20f533193"
+version = "0.5.2"
+
+[[ColorTypes]]
+deps = ["FixedPointNumbers", "Random"]
+git-tree-sha1 = "10050a24b09e8e41b951e9976b109871ce98d965"
+uuid = "3da002f7-5984-5a60-b8a6-cbb66c0b333f"
+version = "0.8.0"
+
+[[Colors]]
+deps = ["ColorTypes", "FixedPointNumbers", "InteractiveUtils", "Printf", "Reexport", "Test"]
+git-tree-sha1 = "9f0a0210450acb91c730b730a994f8eef1d3d543"
+uuid = "5ae59095-9a9b-59fe-a467-6f913c188581"
+version = "0.9.5"
+
+[[CommonSubexpressions]]
+deps = ["Test"]
+git-tree-sha1 = "efdaf19ab11c7889334ca247ff4c9f7c322817b0"
+uuid = "bbf7d656-a473-5ed7-a52c-81e309532950"
+version = "0.2.0"
+
+[[Compat]]
+deps = ["Base64", "Dates", "DelimitedFiles", "Distributed", "InteractiveUtils", "LibGit2", "Libdl", "LinearAlgebra", "Markdown", "Mmap", "Pkg", "Printf", "REPL", "Random", "Serialization", "SharedArrays", "Sockets", "SparseArrays", "Statistics", "Test", "UUIDs", "Unicode"]
+git-tree-sha1 = "84aa74986c5b9b898b0d1acaf3258741ee64754f"
+uuid = "34da2185-b29b-5c13-b0c7-acf172513d20"
+version = "2.1.0"
+
+[[Contour]]
+deps = ["LinearAlgebra", "StaticArrays", "Test"]
+git-tree-sha1 = "b974e164358fea753ef853ce7bad97afec15bb80"
+uuid = "d38c429a-6771-53c6-b99e-75d170b6e991"
+version = "0.5.1"
+
+[[Crayons]]
+deps = ["Test"]
+git-tree-sha1 = "f621b8ef51fd2004c7cf157ea47f027fdeac5523"
+uuid = "a8cc5b0e-0ffa-5ad4-8c14-923d3ee1735f"
+version = "4.0.0"
+
+[[DataFrames]]
+deps = ["CategoricalArrays", "Compat", "IteratorInterfaceExtensions", "Missings", "PooledArrays", "Printf", "REPL", "Reexport", "SortingAlgorithms", "Statistics", "StatsBase", "TableTraits", "Tables", "Unicode"]
+git-tree-sha1 = "7c0f86a01be0f77cc7f3f9096ed875f1217487e1"
+uuid = "a93c6f00-e57d-5684-b7b6-d8193f3e46c0"
+version = "0.18.4"
+
+[[DataStructures]]
+deps = ["InteractiveUtils", "OrderedCollections", "Random", "Serialization", "Test"]
+git-tree-sha1 = "ca971f03e146cf144a9e2f2ce59674f5bf0e8038"
+uuid = "864edb3b-99cc-5e75-8d2d-829cb0a9cfe8"
+version = "0.15.0"
+
+[[DataValueInterfaces]]
+git-tree-sha1 = "bfc1187b79289637fa0ef6d4436ebdfe6905cbd6"
+uuid = "e2d170a0-9d28-54be-80f0-106bbe20a464"
+version = "1.0.0"
+
+[[Dates]]
+deps = ["Printf"]
+uuid = "ade2ca70-3891-5945-98fb-dc099432e06a"
+
+[[DelayDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "ForwardDiff", "MuladdMacro", "NLSolversBase", "OrdinaryDiffEq", "RecursiveArrayTools", "Reexport", "Roots"]
+git-tree-sha1 = "d933682653f8c3c922592d75e50b5a30689ede6d"
+uuid = "bcd4f6db-9728-5f36-b5f7-82caef46ccdb"
+version = "5.4.1"
+
+[[DelimitedFiles]]
+deps = ["Mmap"]
+uuid = "8bb1440f-4735-579b-a4ab-409b98df4dab"
+
+[[DiffEqBase]]
+deps = ["Compat", "Distributed", "DocStringExtensions", "FunctionWrappers", "IterativeSolvers", "IteratorInterfaceExtensions", "LinearAlgebra", "MuladdMacro", "Parameters", "RecipesBase", "RecursiveArrayTools", "RecursiveFactorization", "Requires", "Roots", "SparseArrays", "StaticArrays", "Statistics", "SuiteSparse", "TableTraits", "TreeViews"]
+git-tree-sha1 = "3c08441014d2e1bad515df5443dd2d0ba379888c"
+uuid = "2b5f629d-d688-5b77-993f-72d75c75574e"
+version = "5.12.0"
+
+[[DiffEqCallbacks]]
+deps = ["DataStructures", "DiffEqBase", "LinearAlgebra", "OrdinaryDiffEq", "RecipesBase", "RecursiveArrayTools", "StaticArrays", "Test"]
+git-tree-sha1 = "027a13f010f2a93b2df725b7f6202590ce6f559d"
+uuid = "459566f4-90b8-5000-8ac3-15dfb0a30def"
+version = "2.5.2"
+
+[[DiffEqDiffTools]]
+deps = ["LinearAlgebra", "SparseArrays", "StaticArrays"]
+git-tree-sha1 = "2d4f49c1839c1f30e4820400d8c109c6b16e869a"
+uuid = "01453d9d-ee7c-5054-8395-0335cb756afa"
+version = "0.13.0"
+
+[[DiffEqFinancial]]
+deps = ["DiffEqBase", "DiffEqNoiseProcess", "LinearAlgebra", "Markdown", "RandomNumbers", "Test"]
+git-tree-sha1 = "f250512b982b771f6bdb3df05b89df314f2c2580"
+uuid = "5a0ffddc-d203-54b0-88ba-2c03c0fc2e67"
+version = "2.1.0"
+
+[[DiffEqFlux]]
+deps = ["Adapt", "DiffEqBase", "DiffEqSensitivity", "DiffResults", "Flux", "ForwardDiff", "RecursiveArrayTools", "Requires"]
+git-tree-sha1 = "1c311e6a4f14c70c7ea33482db9856392c4b6b80"
+uuid = "aae7a2af-3d4f-5e19-a356-7da93b79d9d0"
+version = "0.5.0"
+
+[[DiffEqJump]]
+deps = ["Compat", "DataStructures", "DiffEqBase", "FunctionWrappers", "LinearAlgebra", "Parameters", "PoissonRandom", "Random", "RandomNumbers", "RecursiveArrayTools", "Statistics", "Test", "TreeViews"]
+git-tree-sha1 = "784b979eeca8e9586aea9e63edbdcf5573bf9449"
+uuid = "c894b116-72e5-5b58-be3c-e6d8d4ac2b12"
+version = "6.1.1"
+
+[[DiffEqMonteCarlo]]
+deps = ["DiffEqBase", "Distributed", "RecursiveArrayTools", "StaticArrays", "Statistics"]
+git-tree-sha1 = "edffd3e114b5c2cad15e7790db6d82f69e3f42ae"
+uuid = "78ddff82-25fc-5f2b-89aa-309469cbf16f"
+version = "0.15.1"
+
+[[DiffEqNoiseProcess]]
+deps = ["DataStructures", "DiffEqBase", "LinearAlgebra", "Random", "RandomNumbers", "RecipesBase", "RecursiveArrayTools", "Requires", "ResettableStacks", "StaticArrays", "Statistics"]
+git-tree-sha1 = "f5333c0aa6208680e48cd24ae6f759c262a1cf85"
+uuid = "77a26b50-5914-5dd7-bc55-306e6241c503"
+version = "3.3.1"
+
+[[DiffEqOperators]]
+deps = ["DiffEqBase", "ForwardDiff", "LinearAlgebra", "SparseArrays", "StaticArrays", "SuiteSparse"]
+git-tree-sha1 = "2884a79a72aac38347b247615ac42eda41aa36e0"
+uuid = "9fdde737-9c7f-55bf-ade8-46b3f136cc48"
+version = "3.5.0"
+
+[[DiffEqPhysics]]
+deps = ["Dates", "DiffEqBase", "DiffEqCallbacks", "ForwardDiff", "LinearAlgebra", "Printf", "Random", "RecipesBase", "RecursiveArrayTools", "Reexport", "StaticArrays", "Test"]
+git-tree-sha1 = "d3dbc53318a6477f496ae2347db98c3ded36c486"
+uuid = "055956cb-9e8b-5191-98cc-73ae4a59e68a"
+version = "3.1.0"
+
+[[DiffEqSensitivity]]
+deps = ["DataFrames", "DiffEqBase", "DiffEqCallbacks", "DiffEqDiffTools", "Flux", "ForwardDiff", "GLM", "LinearAlgebra", "QuadGK", "RecursiveArrayTools", "Statistics"]
+git-tree-sha1 = "09c964dc242f295180dd99d89fb2f259927029ef"
+uuid = "41bf760c-e81c-5289-8e54-58b1f1f8abe2"
+version = "3.2.4"
+
+[[DiffResults]]
+deps = ["Compat", "StaticArrays"]
+git-tree-sha1 = "34a4a1e8be7bc99bc9c611b895b5baf37a80584c"
+uuid = "163ba53b-c6d8-5494-b064-1a9d43ac40c5"
+version = "0.0.4"
+
+[[DiffRules]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "dc0869fb2f5b23466b32ea799bd82c76480167f7"
+uuid = "b552c78f-8df3-52c6-915a-8e097449b14b"
+version = "0.0.10"
+
+[[DifferentialEquations]]
+deps = ["BoundaryValueDiffEq", "DelayDiffEq", "DiffEqBase", "DiffEqCallbacks", "DiffEqFinancial", "DiffEqJump", "DiffEqMonteCarlo", "DiffEqNoiseProcess", "DiffEqPhysics", "DimensionalPlotRecipes", "LinearAlgebra", "MultiScaleArrays", "OrdinaryDiffEq", "Random", "RecursiveArrayTools", "Reexport", "SteadyStateDiffEq", "StochasticDiffEq", "Sundials"]
+git-tree-sha1 = "e5b3ca6afe2a064bdfecba483999ee75d81750c6"
+uuid = "0c46a032-eb83-5123-abaf-570d42b7fbaa"
+version = "6.4.0"
+
+[[DimensionalPlotRecipes]]
+deps = ["LinearAlgebra", "RecipesBase", "Test"]
+git-tree-sha1 = "d348688f9a3d02c24455327231c450c272b7401c"
+uuid = "c619ae07-58cd-5f6d-b883-8f17bd6a98f9"
+version = "0.2.0"
+
+[[Distances]]
+deps = ["LinearAlgebra", "Printf", "Random", "Statistics", "Test"]
+git-tree-sha1 = "a135c7c062023051953141da8437ed74f89d767a"
+uuid = "b4f34e82-e78d-54a5-968a-f98e89d6e8f7"
+version = "0.8.0"
+
+[[Distributed]]
+deps = ["Random", "Serialization", "Sockets"]
+uuid = "8ba89e20-285c-5b6f-9357-94700520ee1b"
+
+[[Distributions]]
+deps = ["LinearAlgebra", "PDMats", "Printf", "QuadGK", "Random", "SpecialFunctions", "Statistics", "StatsBase", "StatsFuns"]
+git-tree-sha1 = "56a158bc0abe4af5d4027af2275fde484261ca6d"
+uuid = "31c24e10-a181-5473-b8eb-7969acd0382f"
+version = "0.19.2"
+
+[[DocStringExtensions]]
+deps = ["LibGit2", "Markdown", "Pkg", "Test"]
+git-tree-sha1 = "0513f1a8991e9d83255e0140aace0d0fc4486600"
+uuid = "ffbed154-4ef7-542d-bbb7-c09d3a79fcae"
+version = "0.8.0"
+
+[[ExponentialUtilities]]
+deps = ["LinearAlgebra", "Printf", "SparseArrays"]
+git-tree-sha1 = "85e1ce16aa9b98793df704e17e7a0ceadefe404f"
+uuid = "d4d017d3-3776-5f7e-afef-a10c40355c18"
+version = "1.5.1"
+
+[[FileWatching]]
+uuid = "7b1f6079-737a-58dc-b8bc-7a2ca5c1b5ee"
+
+[[FillArrays]]
+deps = ["LinearAlgebra", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "9ab8f76758cbabba8d7f103c51dce7f73fcf8e92"
+uuid = "1a297f60-69ca-5386-bcde-b61e274b549b"
+version = "0.6.3"
+
+[[FixedPointNumbers]]
+git-tree-sha1 = "d14a6fa5890ea3a7e5dcab6811114f132fec2b4b"
+uuid = "53c48c17-4a7d-5ca2-90c5-79b7896eea93"
+version = "0.6.1"
+
+[[Flux]]
+deps = ["AbstractTrees", "Adapt", "CodecZlib", "Colors", "DelimitedFiles", "Juno", "LinearAlgebra", "MacroTools", "NNlib", "Pkg", "Printf", "Random", "Reexport", "Requires", "SHA", "Statistics", "StatsBase", "Tracker", "ZipFile"]
+git-tree-sha1 = "08212989c2856f95f90709ea5fd824bd27b34514"
+uuid = "587475ba-b771-5e3f-ad9e-33799f191a9c"
+version = "0.8.3"
+
+[[ForwardDiff]]
+deps = ["CommonSubexpressions", "DiffResults", "DiffRules", "InteractiveUtils", "LinearAlgebra", "NaNMath", "Random", "SparseArrays", "SpecialFunctions", "StaticArrays", "Test"]
+git-tree-sha1 = "4c4d727f1b7e0092134fabfab6396b8945c1ea5b"
+repo-rev = "master"
+repo-url = "https://github.com/JuliaDiff/ForwardDiff.jl.git"
+uuid = "f6369f11-7733-5829-9624-2563aa707210"
+version = "0.10.3+"
+
+[[FunctionWrappers]]
+deps = ["Compat"]
+git-tree-sha1 = "49bf793ebd37db5adaa7ac1eae96c2c97ec86db5"
+uuid = "069b7b12-0de2-55c6-9aab-29f3d0a68a2e"
+version = "1.0.0"
+
+[[FunctionalCollections]]
+deps = ["Test"]
+git-tree-sha1 = "04cb9cfaa6ba5311973994fe3496ddec19b6292a"
+uuid = "de31a74c-ac4f-5751-b3fd-e18cd04993ca"
+version = "0.5.0"
+
+[[Future]]
+deps = ["Random"]
+uuid = "9fa8497b-333b-5362-9e8d-4d0656e87820"
+
+[[GLM]]
+deps = ["Distributions", "LinearAlgebra", "Printf", "Random", "Reexport", "SparseArrays", "SpecialFunctions", "Statistics", "StatsBase", "StatsFuns", "StatsModels"]
+git-tree-sha1 = "bb918f52a8e2131857ddac319033610bb3be35a4"
+uuid = "38e38edf-8417-5370-95a0-9cbb8c7f171a"
+version = "1.3.0"
+
+[[GR]]
+deps = ["Base64", "DelimitedFiles", "LinearAlgebra", "Pkg", "Printf", "Random", "Serialization", "Sockets", "Test"]
+git-tree-sha1 = "9dff2d231311da78648abfa3287e3458a578d2f8"
+uuid = "28b8d3ca-fb5f-59d9-8090-bfdbd6d07a71"
+version = "0.40.0"
+
+[[GenericSVD]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "8aa93c3f3d81562a8962047eafcc5712af0a0f59"
+uuid = "01680d73-4ee2-5a08-a1aa-533608c188bb"
+version = "0.2.1"
+
+[[GeometryTypes]]
+deps = ["ColorTypes", "FixedPointNumbers", "IterTools", "LinearAlgebra", "StaticArrays"]
+git-tree-sha1 = "2b0bfb379a54bdfcd2942f388f7d045f8952373d"
+uuid = "4d00f742-c7ba-57c2-abde-4428a4b178cb"
+version = "0.7.5"
+
+[[HTTP]]
+deps = ["Base64", "Dates", "IniFile", "MbedTLS", "Sockets"]
+git-tree-sha1 = "6e59e7ec3c71eda9e0261c98896da5d3d008fa7d"
+uuid = "cd3eb016-35fb-5094-929b-558a96fad6f3"
+version = "0.8.3"
+
+[[IRTools]]
+deps = ["InteractiveUtils", "MacroTools", "Test"]
+git-tree-sha1 = "a9b1fc7745ae4745a634bbb6d1cb7fd64e37248a"
+uuid = "7869d1d1-7146-5819-86e3-90919afe41df"
+version = "0.2.2"
+
+[[IniFile]]
+deps = ["Test"]
+git-tree-sha1 = "098e4d2c533924c921f9f9847274f2ad89e018b8"
+uuid = "83e8ac13-25f8-5344-8a64-a9f2b223428f"
+version = "0.5.0"
+
+[[InteractiveUtils]]
+deps = ["Markdown"]
+uuid = "b77e0a4c-d291-57a0-90e8-8db25a27a240"
+
+[[IterTools]]
+deps = ["SparseArrays", "Test"]
+git-tree-sha1 = "79246285c43602384e6f1943b3554042a3712056"
+uuid = "c8e1da08-722c-5040-9ed9-7db0dc04731e"
+version = "1.1.1"
+
+[[IterativeSolvers]]
+deps = ["LinearAlgebra", "Printf", "Random", "RecipesBase", "SparseArrays", "Test"]
+git-tree-sha1 = "5687f68018b4f14c0da54d402bb23eecaec17f37"
+uuid = "42fd0dbc-a981-5370-80f2-aaf504508153"
+version = "0.8.1"
+
+[[IteratorInterfaceExtensions]]
+git-tree-sha1 = "a3f24677c21f5bbe9d2a714f95dcd58337fb2856"
+uuid = "82899510-4779-5014-852e-03e436cf321d"
+version = "1.0.0"
+
+[[JSExpr]]
+deps = ["JSON", "MacroTools", "Observables", "Test", "WebIO"]
+git-tree-sha1 = "013bc2143a2e84ea489365cf30db3407deb540c2"
+uuid = "97c1335a-c9c5-57fe-bc5d-ec35cebe8660"
+version = "0.5.0"
+
+[[JSON]]
+deps = ["Dates", "Distributed", "Mmap", "Sockets", "Test", "Unicode"]
+git-tree-sha1 = "1f7a25b53ec67f5e9422f1f551ee216503f4a0fa"
+uuid = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
+version = "0.20.0"
+
+[[Juno]]
+deps = ["Base64", "Logging", "Media", "Profile", "Test"]
+git-tree-sha1 = "4e4a8d43aa7ecec66cadaf311fbd1e5c9d7b9175"
+uuid = "e5e0dc1b-0480-54bc-9374-aad01c23163d"
+version = "0.7.0"
+
+[[LazyArrays]]
+deps = ["FillArrays", "LinearAlgebra", "MacroTools", "StaticArrays", "Test"]
+git-tree-sha1 = "5eec856c454496abe8f4504227fcc187205a502a"
+uuid = "5078a376-72f3-5289-bfd5-ec5146d43c02"
+version = "0.9.0"
+
+[[LibGit2]]
+uuid = "76f85450-5226-5b5a-8eaa-529ad045b433"
+
+[[Libdl]]
+uuid = "8f399da3-3557-5675-b5ff-fb832c97cbdb"
+
+[[LineSearches]]
+deps = ["LinearAlgebra", "NLSolversBase", "NaNMath", "Parameters", "Printf", "Test"]
+git-tree-sha1 = "54eb90e8dbe745d617c78dee1d6ae95c7f6f5779"
+uuid = "d3d80556-e9d4-5f37-9878-2ab0fcc64255"
+version = "7.0.1"
+
+[[LinearAlgebra]]
+deps = ["Libdl"]
+uuid = "37e2e46d-f89d-539d-b4ee-838fcccc9c8e"
+
+[[Literate]]
+deps = ["Base64", "JSON", "REPL", "Test"]
+git-tree-sha1 = "021e2e3106713e22a7f3769ebf9f2f4469670444"
+uuid = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
+version = "1.1.0"
+
+[[Logging]]
+uuid = "56ddb016-857b-54e1-b83d-db4d58db5568"
+
+[[MacroTools]]
+deps = ["CSTParser", "Compat", "DataStructures", "Test"]
+git-tree-sha1 = "daecd9e452f38297c686eba90dba2a6d5da52162"
+uuid = "1914dd2f-81c6-5fcd-8719-6d5c9610ff09"
+version = "0.5.0"
+
+[[Markdown]]
+deps = ["Base64"]
+uuid = "d6f4376e-aef5-505a-96c1-9c027394607a"
+
+[[MatrixFactorizations]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "cebc71d929a846dda61400f1cf3ba69c7e75fa63"
+uuid = "a3b82374-2e81-5b9e-98ce-41277c0e4c87"
+version = "0.0.4"
+
+[[MbedTLS]]
+deps = ["BinaryProvider", "Dates", "Libdl", "Random", "Sockets"]
+git-tree-sha1 = "85f5947b53c8cfd53ccfa3f4abae31faa22c2181"
+uuid = "739be429-bea8-5141-9913-cc70e7f3736d"
+version = "0.7.0"
+
+[[Measures]]
+deps = ["Test"]
+git-tree-sha1 = "ddfd6d13e330beacdde2c80de27c1c671945e7d9"
+uuid = "442fdcdd-2543-5da2-b0f3-8c86c306513e"
+version = "0.3.0"
+
+[[Media]]
+deps = ["MacroTools", "Test"]
+git-tree-sha1 = "75a54abd10709c01f1b86b84ec225d26e840ed58"
+uuid = "e89f7d12-3494-54d1-8411-f7d8b9ae1f27"
+version = "0.5.0"
+
+[[Missings]]
+deps = ["SparseArrays", "Test"]
+git-tree-sha1 = "f0719736664b4358aa9ec173077d4285775f8007"
+uuid = "e1d29d7a-bbdc-5cf2-9ac0-f12de2c33e28"
+version = "0.4.1"
+
+[[Mmap]]
+uuid = "a63ad114-7e13-5084-954f-fe012c677804"
+
+[[MuladdMacro]]
+deps = ["MacroTools", "Test"]
+git-tree-sha1 = "41e6e7c4b448afeaddaac7f496b414854f83b848"
+uuid = "46d2c3a1-f734-5fdb-9937-b9b9aeba4221"
+version = "0.2.1"
+
+[[MultiScaleArrays]]
+deps = ["DiffEqBase", "LinearAlgebra", "RecursiveArrayTools", "Statistics", "StochasticDiffEq", "Test", "TreeViews"]
+git-tree-sha1 = "4220ceea71186db2bb45cb817984c99e563f3662"
+uuid = "f9640e96-87f6-5992-9c3b-0743c6a49ffa"
+version = "1.4.0"
+
+[[NLSolversBase]]
+deps = ["Calculus", "DiffEqDiffTools", "DiffResults", "Distributed", "ForwardDiff", "LinearAlgebra", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "0c6f0e7f2178f78239cfb75310359eed10f2cacb"
+uuid = "d41bc354-129a-5804-8e4c-c37616107c6c"
+version = "7.3.1"
+
+[[NLsolve]]
+deps = ["DiffEqDiffTools", "Distances", "ForwardDiff", "LineSearches", "LinearAlgebra", "NLSolversBase", "Printf", "Random", "Reexport", "SparseArrays", "Test"]
+git-tree-sha1 = "413e54f04a4cbe9804089794eec6b06b2a43bc47"
+uuid = "2774e3e8-f4cf-5e23-947b-6d7e65073b56"
+version = "4.0.0"
+
+[[NNlib]]
+deps = ["Libdl", "LinearAlgebra", "Requires", "Statistics", "TimerOutputs"]
+git-tree-sha1 = "0c667371391fc6bb31f7f12f96a56a17098b3de8"
+uuid = "872c559c-99b0-510c-b3b7-b6c96a88d5cd"
+version = "0.6.0"
+
+[[NaNMath]]
+deps = ["Compat"]
+git-tree-sha1 = "ce3b85e484a5d4c71dd5316215069311135fa9f2"
+uuid = "77ba4419-2d1f-58cd-9bb1-8ffee604a2e3"
+version = "0.3.2"
+
+[[Observables]]
+deps = ["Test"]
+git-tree-sha1 = "dc02cec22747d1d10d9f70d8a1c03432b5bfbcd0"
+uuid = "510215fc-4207-5dde-b226-833fc4488ee2"
+version = "0.2.3"
+
+[[OffsetArrays]]
+git-tree-sha1 = "1af2f79c7eaac3e019a0de41ef63335ff26a0a57"
+uuid = "6fe1bfb0-de20-5000-8ca7-80f57d26f881"
+version = "0.11.1"
+
+[[Optim]]
+deps = ["Calculus", "DiffEqDiffTools", "ForwardDiff", "LineSearches", "LinearAlgebra", "NLSolversBase", "NaNMath", "Parameters", "PositiveFactorizations", "Printf", "Random", "SparseArrays", "StatsBase", "Test"]
+git-tree-sha1 = "a626e09c1f7f019b8f3a30a8172c7b82d2f4810b"
+uuid = "429524aa-4258-5aef-a3af-852621145aeb"
+version = "0.18.1"
+
+[[OrderedCollections]]
+deps = ["Random", "Serialization", "Test"]
+git-tree-sha1 = "c4c13474d23c60d20a67b217f1d7f22a40edf8f1"
+uuid = "bac558e1-5e72-5ebc-8fee-abe8a469f55d"
+version = "1.1.0"
+
+[[OrdinaryDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "DiffEqOperators", "ExponentialUtilities", "ForwardDiff", "GenericSVD", "LinearAlgebra", "Logging", "MuladdMacro", "NLsolve", "Parameters", "RecursiveArrayTools", "Reexport", "StaticArrays"]
+git-tree-sha1 = "7481f05badc75b80a62d0da988f09d6028c4fbb1"
+uuid = "1dea7af3-3e70-54e6-95c3-0bf5283fa5ed"
+version = "5.8.1"
+
+[[PDMats]]
+deps = ["Arpack", "LinearAlgebra", "SparseArrays", "SuiteSparse", "Test"]
+git-tree-sha1 = "8b68513175b2dc4023a564cb0e917ce90e74fd69"
+uuid = "90014a1f-27ba-587c-ab20-58faa44d9150"
+version = "0.9.7"
+
+[[Parameters]]
+deps = ["Markdown", "OrderedCollections", "REPL", "Test"]
+git-tree-sha1 = "70bdbfb2bceabb15345c0b54be4544813b3444e4"
+uuid = "d96e819e-fc66-5662-9728-84c9c7592b0a"
+version = "0.10.3"
+
+[[Parsers]]
+deps = ["Dates", "Test"]
+git-tree-sha1 = "db2b35dedab3c0e46dc15996d170af07a5ab91c9"
+uuid = "69de0a69-1ddd-5017-9359-2bf0b02dc9f0"
+version = "0.3.6"
+
+[[Pidfile]]
+deps = ["FileWatching", "Test"]
+git-tree-sha1 = "1ffd82728498b5071cde851bbb7abd780d4445f3"
+uuid = "fa939f87-e72e-5be4-a000-7fc836dbe307"
+version = "1.1.0"
+
+[[Pkg]]
+deps = ["Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "UUIDs"]
+uuid = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
+
+[[PlotThemes]]
+deps = ["PlotUtils", "Requires", "Test"]
+git-tree-sha1 = "f3afd2d58e1f6ac9be2cea46e4a9083ccc1d990b"
+uuid = "ccf2f8ad-2431-5c83-bf29-c5338b663b6a"
+version = "0.3.0"
+
+[[PlotUtils]]
+deps = ["Colors", "Dates", "Printf", "Random", "Reexport", "Test"]
+git-tree-sha1 = "8e87bbb778c26f575fbe47fd7a49c7b5ca37c0c6"
+uuid = "995b91a9-d308-5afd-9ec6-746e21dbc043"
+version = "0.5.8"
+
+[[Plots]]
+deps = ["Base64", "Contour", "Dates", "FixedPointNumbers", "GR", "GeometryTypes", "JSON", "LinearAlgebra", "Measures", "NaNMath", "Pkg", "PlotThemes", "PlotUtils", "Printf", "REPL", "Random", "RecipesBase", "Reexport", "Requires", "Showoff", "SparseArrays", "Statistics", "StatsBase", "UUIDs"]
+git-tree-sha1 = "c446e51959578de01b5a4efa72ca6f2460e38196"
+uuid = "91a5bcdd-55d7-5caf-9e0b-520d859cae80"
+version = "0.25.1"
+
+[[PoissonRandom]]
+deps = ["Random", "Statistics", "Test"]
+git-tree-sha1 = "44d018211a56626288b5d3f8c6497d28c26dc850"
+uuid = "e409e4f3-bfea-5376-8464-e040bb5c01ab"
+version = "0.4.0"
+
+[[PooledArrays]]
+git-tree-sha1 = "6e8c38927cb6e9ae144f7277c753714861b27d14"
+uuid = "2dfb63ee-cc39-5dd5-95bd-886bf059d720"
+version = "0.5.2"
+
+[[PositiveFactorizations]]
+deps = ["LinearAlgebra", "Test"]
+git-tree-sha1 = "957c3dd7c33895469760ce873082fbb6b3620641"
+uuid = "85a6dd25-e78a-55b7-8502-1745935b8125"
+version = "0.2.2"
+
+[[Printf]]
+deps = ["Unicode"]
+uuid = "de0858da-6303-5e67-8744-51eddeeeb8d7"
+
+[[Profile]]
+deps = ["Printf"]
+uuid = "9abbd945-dff8-562f-b5e8-e1ebf5ef1b79"
+
+[[QuadGK]]
+deps = ["DataStructures", "LinearAlgebra"]
+git-tree-sha1 = "438630b843c210b375b2a246329200c113acc61b"
+uuid = "1fd47b50-473d-5c70-9696-f719f8f3bcdc"
+version = "2.1.0"
+
+[[REPL]]
+deps = ["InteractiveUtils", "Markdown", "Sockets"]
+uuid = "3fa0cd96-eef1-5676-8a61-b3b8758bbffb"
+
+[[Random]]
+deps = ["Serialization"]
+uuid = "9a3f8284-a2c9-5f02-9a11-845980a1fd5c"
+
+[[RandomNumbers]]
+deps = ["Random", "Requires"]
+git-tree-sha1 = "1417be19c15706c1584d01e32662eb640a4cc908"
+uuid = "e6cf234a-135c-5ec9-84dd-332b85af5143"
+version = "1.3.0"
+
+[[RecipesBase]]
+git-tree-sha1 = "7bdce29bc9b2f5660a6e5e64d64d91ec941f6aa2"
+uuid = "3cdcf5f2-1ef4-517c-9805-6587b60abb01"
+version = "0.7.0"
+
+[[RecursiveArrayTools]]
+deps = ["ArrayInterface", "RecipesBase", "Requires", "StaticArrays", "Statistics", "Test"]
+git-tree-sha1 = "187ea7dd541955102c7035a6668613bdf52022ca"
+uuid = "731186ca-8d62-57ce-b412-fbd966d074cd"
+version = "0.20.0"
+
+[[RecursiveFactorization]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "54410ebd72cbb84d7b7678eb3da643f8e71181fc"
+uuid = "f2c3362d-daeb-58d1-803e-2bc74f2840b4"
+version = "0.0.1"
+
+[[Reexport]]
+deps = ["Pkg"]
+git-tree-sha1 = "7b1d07f411bc8ddb7977ec7f377b97b158514fe0"
+uuid = "189a3867-3050-52da-a836-e630ba90ab69"
+version = "0.2.0"
+
+[[Requires]]
+deps = ["Test"]
+git-tree-sha1 = "f6fbf4ba64d295e146e49e021207993b6b48c7d1"
+uuid = "ae029012-a4dd-5104-9daa-d747884805df"
+version = "0.5.2"
+
+[[ResettableStacks]]
+deps = ["Random", "StaticArrays", "Test"]
+git-tree-sha1 = "8b4f6cf3c97530e1ba7177ad3bc2b134373da851"
+uuid = "ae5879a3-cd67-5da8-be7f-38c6eb64a37b"
+version = "0.6.0"
+
+[[Rmath]]
+deps = ["BinaryProvider", "Libdl", "Random", "Statistics", "Test"]
+git-tree-sha1 = "9a6c758cdf73036c3239b0afbea790def1dabff9"
+uuid = "79098fc4-a85e-5d69-aa6a-4863f24498fa"
+version = "0.5.0"
+
+[[Roots]]
+deps = ["Printf", "Statistics", "Test"]
+git-tree-sha1 = "7228278e31d6d0e22a1ae0b41ea9a0df2859f33d"
+uuid = "f2b01f46-fcfa-551c-844a-d8ac1e96c665"
+version = "0.8.1"
+
+[[SHA]]
+uuid = "ea8e919c-243c-51af-8825-aaa63cd721ce"
+
+[[Serialization]]
+uuid = "9e88b42a-f829-5b0c-bbe9-9e923198166b"
+
+[[SharedArrays]]
+deps = ["Distributed", "Mmap", "Random", "Serialization"]
+uuid = "1a1011a3-84de-559e-8e89-a11a2f7dc383"
+
+[[ShiftedArrays]]
+deps = ["OffsetArrays", "RecursiveArrayTools", "Test"]
+git-tree-sha1 = "b1aa84666a23a31cebcdcb848e62428968789287"
+uuid = "1277b4bf-5013-50f5-be3d-901d8477a67a"
+version = "0.5.0"
+
+[[Showoff]]
+deps = ["Dates"]
+git-tree-sha1 = "e032c9df551fb23c9f98ae1064de074111b7bc39"
+uuid = "992d4aef-0814-514b-bc4d-f2e9a6c4116f"
+version = "0.3.1"
+
+[[Sockets]]
+uuid = "6462fe0b-24de-5631-8697-dd941f90decc"
+
+[[SortingAlgorithms]]
+deps = ["DataStructures", "Random", "Test"]
+git-tree-sha1 = "03f5898c9959f8115e30bc7226ada7d0df554ddd"
+uuid = "a2af1166-a08f-5f64-846c-94a0d3cef48c"
+version = "0.3.1"
+
+[[SparseArrays]]
+deps = ["LinearAlgebra", "Random"]
+uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
+
+[[SpecialFunctions]]
+deps = ["BinDeps", "BinaryProvider", "Libdl", "Test"]
+git-tree-sha1 = "0b45dc2e45ed77f445617b99ff2adf0f5b0f23ea"
+uuid = "276daf66-3868-5448-9aa4-cd146d93841b"
+version = "0.7.2"
+
+[[StaticArrays]]
+deps = ["LinearAlgebra", "Random", "Statistics"]
+git-tree-sha1 = "db23bbf50064c582b6f2b9b043c8e7e98ea8c0c6"
+uuid = "90137ffa-7385-5640-81b9-e52037218182"
+version = "0.11.0"
+
+[[Statistics]]
+deps = ["LinearAlgebra", "SparseArrays"]
+uuid = "10745b16-79ce-11e8-11f9-7d13ad32a3b2"
+
+[[StatsBase]]
+deps = ["DataStructures", "LinearAlgebra", "Missings", "Printf", "Random", "SortingAlgorithms", "SparseArrays", "Statistics"]
+git-tree-sha1 = "8a0f4b09c7426478ab677245ab2b0b68552143c7"
+uuid = "2913bbd2-ae8a-5f71-8c99-4fb6c76f3a91"
+version = "0.30.0"
+
+[[StatsFuns]]
+deps = ["Rmath", "SpecialFunctions", "Test"]
+git-tree-sha1 = "b3a4e86aa13c732b8a8c0ba0c3d3264f55e6bb3e"
+uuid = "4c63d2b9-4356-54db-8cca-17b64c39e42c"
+version = "0.8.0"
+
+[[StatsModels]]
+deps = ["CategoricalArrays", "DataStructures", "LinearAlgebra", "Missings", "ShiftedArrays", "SparseArrays", "StatsBase", "Tables"]
+git-tree-sha1 = "f004c23db67aeecb4bba94d08c79580af851b21b"
+uuid = "3eaba693-59b7-5ba5-a881-562e759f1c8d"
+version = "0.6.1"
+
+[[SteadyStateDiffEq]]
+deps = ["Compat", "DiffEqBase", "DiffEqCallbacks", "LinearAlgebra", "NLsolve", "Reexport", "Test"]
+git-tree-sha1 = "fe9852d18c3e30f384003da50d6049e5fbc97071"
+uuid = "9672c7b4-1e72-59bd-8a11-6ac3964bc41f"
+version = "1.4.0"
+
+[[StochasticDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "DiffEqNoiseProcess", "DiffEqOperators", "FillArrays", "ForwardDiff", "LinearAlgebra", "Logging", "MuladdMacro", "NLsolve", "Parameters", "Random", "RandomNumbers", "RecursiveArrayTools", "Reexport", "StaticArrays"]
+git-tree-sha1 = "83be179dc849f11f83dcfa715c7818ef551a0f6c"
+uuid = "789caeaf-c7a9-5a7d-9973-96adeb23e2a0"
+version = "6.5.0"
+
+[[SuiteSparse]]
+deps = ["Libdl", "LinearAlgebra", "Serialization", "SparseArrays"]
+uuid = "4607b0f0-06f3-5cda-b6b1-a6196a1729e9"
+
+[[Sundials]]
+deps = ["BinaryProvider", "DataStructures", "DiffEqBase", "Libdl", "LinearAlgebra", "Logging", "Reexport", "SparseArrays", "SuiteSparse"]
+git-tree-sha1 = "9af4eb72683f0dafe84c6a5bd31aea1ebca4d46c"
+uuid = "c3572dad-4567-51f8-b174-8c6c989267f4"
+version = "3.6.1"
+
+[[TableTraits]]
+deps = ["IteratorInterfaceExtensions"]
+git-tree-sha1 = "b1ad568ba658d8cbb3b892ed5380a6f3e781a81e"
+uuid = "3783bdb8-4a98-5b6b-af9a-565f29a5fe9c"
+version = "1.0.0"
+
+[[Tables]]
+deps = ["DataValueInterfaces", "IteratorInterfaceExtensions", "LinearAlgebra", "Requires", "TableTraits", "Test"]
+git-tree-sha1 = "c93aafd5c45f850c653ec1c45857ba2151835f95"
+uuid = "bd369af6-aec1-5ad0-b16a-f7cc5008161c"
+version = "0.2.7"
+
+[[Test]]
+deps = ["Distributed", "InteractiveUtils", "Logging", "Random"]
+uuid = "8dfed614-e22c-5e08-85e1-65c5234f0b40"
+
+[[TimerOutputs]]
+deps = ["Crayons", "Printf", "Test", "Unicode"]
+git-tree-sha1 = "b80671c06f8f8bae08c55d67b5ce292c5ae2660c"
+uuid = "a759f4b9-e2f1-59dc-863e-4aeb61b1ea8f"
+version = "0.5.0"
+
+[[Tokenize]]
+git-tree-sha1 = "0de343efc07da00cd449d5b04e959ebaeeb3305d"
+uuid = "0796e94c-ce3b-5d07-9a54-7f471281c624"
+version = "0.5.4"
+
+[[Tracker]]
+deps = ["Adapt", "DiffRules", "ForwardDiff", "LinearAlgebra", "MacroTools", "NNlib", "NaNMath", "Printf", "Random", "Requires", "SpecialFunctions", "Statistics", "Test"]
+git-tree-sha1 = "327342fec6e09f68ced0c2dc5731ed475e4b696b"
+uuid = "9f7883ad-71c0-57eb-9f7f-b5c9e6d3789c"
+version = "0.2.2"
+
+[[TranscodingStreams]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "a25d8e5a28c3b1b06d3859f30757d43106791919"
+uuid = "3bb67fe8-82b1-5028-8e26-92a6c54297fa"
+version = "0.9.4"
+
+[[Trebuchet]]
+deps = ["DiffEqBase", "JSExpr", "OrdinaryDiffEq", "WebIO"]
+git-tree-sha1 = "c1daf264ca0c050381be6258b5e311615ea5f250"
+uuid = "98b73d46-197d-11e9-11eb-69a6ff759d3a"
+version = "0.1.0"
+
+[[TreeViews]]
+deps = ["Test"]
+git-tree-sha1 = "8d0d7a3fe2f30d6a7f833a5f19f7c7a5b396eae6"
+uuid = "a2a6695c-b41b-5b7d-aed9-dbfdeacea5d7"
+version = "0.3.0"
+
+[[URIParser]]
+deps = ["Test", "Unicode"]
+git-tree-sha1 = "6ddf8244220dfda2f17539fa8c9de20d6c575b69"
+uuid = "30578b45-9adc-5946-b283-645ec420af67"
+version = "0.4.0"
+
+[[UUIDs]]
+deps = ["Random", "SHA"]
+uuid = "cf7118a7-6976-5b1a-9a39-7adc72f591a4"
+
+[[Unicode]]
+uuid = "4ec0a83e-493e-50e2-b9ac-8f72acf5a8f5"
+
+[[WeakRefStrings]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "9a0bb82eede528debe631b642eeb48a631a69bc2"
+uuid = "ea10d353-3f73-51f8-a26c-33c1cb351aa5"
+version = "0.6.1"
+
+[[WebIO]]
+deps = ["AssetRegistry", "Base64", "Compat", "Distributed", "FunctionalCollections", "JSON", "Logging", "Observables", "Random", "Requires", "Sockets", "UUIDs", "WebSockets", "Widgets"]
+git-tree-sha1 = "458ebbd85da851b01bed01e6321b0d8f4c7044b0"
+uuid = "0f1e0344-ec1d-5b48-a673-e5cf874b6c29"
+version = "0.8.6"
+
+[[WebSockets]]
+deps = ["Base64", "Dates", "Distributed", "HTTP", "Logging", "Random", "Sockets", "Test"]
+git-tree-sha1 = "13f763d38c7a05688938808b49cb29b18b60c8c8"
+uuid = "104b5d7c-a370-577a-8038-80a2059c5097"
+version = "1.5.2"
+
+[[Widgets]]
+deps = ["Colors", "Dates", "Observables", "OrderedCollections", "Test"]
+git-tree-sha1 = "c53befc70c6b91eaa2a9888c2f6ac2d92720a81b"
+uuid = "cc8bc4a8-27d6-5769-a93b-9d913e69aa62"
+version = "0.6.1"
+
+[[ZipFile]]
+deps = ["BinaryProvider", "Libdl", "Printf"]
+git-tree-sha1 = "580ce62b6c14244916cc28ad54f8a2e2886f843d"
+uuid = "a5390f91-8eb1-5f08-bee0-b1d1ffed6cea"
+version = "0.8.3"
+
+[[Zygote]]
+deps = ["DiffRules", "FillArrays", "ForwardDiff", "IRTools", "InteractiveUtils", "LinearAlgebra", "MacroTools", "NNlib", "NaNMath", "Random", "Requires", "SpecialFunctions", "Statistics"]
+git-tree-sha1 = "520d65c5e5554473863d738bde053f5f6769d3be"
+uuid = "e88e6eb3-aa80-5325-afca-941959d7151f"
+version = "0.3.2"
diff --git a/Courses/Differentiable Programming/Project.toml b/Courses/Differentiable Programming/Project.toml
new file mode 100644
index 0000000..3c94cc3
--- /dev/null
+++ b/Courses/Differentiable Programming/Project.toml
@@ -0,0 +1,12 @@
+[deps]
+BenchmarkTools = "6e4b80f9-dd63-53aa-95a3-0cdb28fa8baf"
+CSV = "336ed68f-0bac-5ca0-87d4-7b16caf5d00b"
+DiffEqFlux = "aae7a2af-3d4f-5e19-a356-7da93b79d9d0"
+DifferentialEquations = "0c46a032-eb83-5123-abaf-570d42b7fbaa"
+Flux = "587475ba-b771-5e3f-ad9e-33799f191a9c"
+ForwardDiff = "f6369f11-7733-5829-9624-2563aa707210"
+Literate = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
+Optim = "429524aa-4258-5aef-a3af-852621145aeb"
+Plots = "91a5bcdd-55d7-5caf-9e0b-520d859cae80"
+Trebuchet = "98b73d46-197d-11e9-11eb-69a6ff759d3a"
+Zygote = "e88e6eb3-aa80-5325-afca-941959d7151f"
diff --git a/Manifest.toml b/Manifest.toml
index fb2c933..d0f2265 100644
--- a/Manifest.toml
+++ b/Manifest.toml
@@ -4,8 +4,10 @@
uuid = "2a0f44e3-6c83-55bd-87e4-b1978d98bd5f"
[[BinaryProvider]]
-deps = ["Compat", "CredentialsHandler", "Libdl", "Pkg", "SHA", "TOML", "Test"]
+deps = ["Libdl", "Logging", "SHA"]
+git-tree-sha1 = "8153fd64131cd00a79544bb23788877741f627bb"
uuid = "b99e7846-7c00-51b0-8f62-c81ae34c0232"
+version = "0.5.5"
[[Compat]]
deps = ["Base64", "Dates", "DelimitedFiles", "Distributed", "InteractiveUtils", "LibGit2", "Libdl", "LinearAlgebra", "Markdown", "Mmap", "Pkg", "Printf", "REPL", "Random", "Serialization", "SharedArrays", "Sockets", "SparseArrays", "Statistics", "Test", "UUIDs", "Unicode"]
@@ -13,9 +15,11 @@ git-tree-sha1 = "84aa74986c5b9b898b0d1acaf3258741ee64754f"
uuid = "34da2185-b29b-5c13-b0c7-acf172513d20"
version = "2.1.0"
-[[CredentialsHandler]]
-deps = ["Base64", "HTTP", "TOML"]
-uuid = "864e158e-919d-11e8-198e-cfe890ec4681"
+[[Conda]]
+deps = ["JSON", "VersionParsing"]
+git-tree-sha1 = "9a11d428dcdc425072af4aea19ab1e8c3e01c032"
+uuid = "8f4d0f93-b110-5947-807f-2305c1781a2d"
+version = "1.3.0"
[[Dates]]
deps = ["Printf"]
@@ -26,18 +30,26 @@ deps = ["Mmap"]
uuid = "8bb1440f-4735-579b-a4ab-409b98df4dab"
[[Distributed]]
-deps = ["LinearAlgebra", "Random", "Serialization", "Sockets"]
+deps = ["Random", "Serialization", "Sockets"]
uuid = "8ba89e20-285c-5b6f-9357-94700520ee1b"
-[[HTTP]]
-deps = ["Base64", "Dates", "Distributed", "IniFile", "MbedTLS", "Sockets", "Test"]
-uuid = "cd3eb016-35fb-5094-929b-558a96fad6f3"
+[[FileWatching]]
+uuid = "7b1f6079-737a-58dc-b8bc-7a2ca5c1b5ee"
-[[IniFile]]
-uuid = "83e8ac13-25f8-5344-8a64-a9f2b223428f"
+[[Glob]]
+deps = ["Compat", "Test"]
+git-tree-sha1 = "c72f1fcb7d17426de1e8af2e948dfb3de1116eed"
+uuid = "c27321d9-0574-5035-807b-f59d2c89b15c"
+version = "1.2.0"
+
+[[IJulia]]
+deps = ["Base64", "Conda", "Dates", "InteractiveUtils", "JSON", "Markdown", "MbedTLS", "Pkg", "Printf", "REPL", "Random", "SoftGlobalScope", "Test", "UUIDs", "ZMQ"]
+git-tree-sha1 = "8eb8459d806de665f1347b25e9ad9428c2609f0f"
+uuid = "7073ff75-c697-5162-941a-fcdaad2a7d2a"
+version = "1.18.1"
[[InteractiveUtils]]
-deps = ["LinearAlgebra", "Markdown"]
+deps = ["Markdown"]
uuid = "b77e0a4c-d291-57a0-90e8-8db25a27a240"
[[JSON]]
@@ -46,14 +58,6 @@ git-tree-sha1 = "1f7a25b53ec67f5e9422f1f551ee216503f4a0fa"
uuid = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
version = "0.20.0"
-[[JuliaAcademyData]]
-deps = ["Pkg"]
-git-tree-sha1 = "6cc6db29d6560619be88d0075d697047eb484f92"
-repo-rev = "master"
-repo-url = "https://github.com/JuliaComputing/JuliaAcademyData.jl"
-uuid = "18b7da76-0988-5e3b-acac-6290be3a708f"
-version = "0.1.0"
-
[[LibGit2]]
uuid = "76f85450-5226-5b5a-8eaa-529ad045b433"
@@ -78,14 +82,16 @@ deps = ["Base64"]
uuid = "d6f4376e-aef5-505a-96c1-9c027394607a"
[[MbedTLS]]
-deps = ["BinaryProvider", "Dates", "Libdl", "Pkg", "Random", "Sockets"]
+deps = ["BinaryProvider", "Dates", "Distributed", "Libdl", "Random", "Sockets", "Test"]
+git-tree-sha1 = "2d94286a9c2f52c63a16146bb86fd6cdfbf677c6"
uuid = "739be429-bea8-5141-9913-cc70e7f3736d"
+version = "0.6.8"
[[Mmap]]
uuid = "a63ad114-7e13-5084-954f-fe012c677804"
[[Pkg]]
-deps = ["BinaryProvider", "CredentialsHandler", "Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "TOML", "UUIDs"]
+deps = ["Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "UUIDs"]
uuid = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
[[Printf]]
@@ -113,6 +119,12 @@ uuid = "1a1011a3-84de-559e-8e89-a11a2f7dc383"
[[Sockets]]
uuid = "6462fe0b-24de-5631-8697-dd941f90decc"
+[[SoftGlobalScope]]
+deps = ["Test"]
+git-tree-sha1 = "012661b70364840fcd380912d878d96f7bf95ff3"
+uuid = "b85f4697-e234-5449-a836-ec8e2f98b302"
+version = "1.0.10"
+
[[SparseArrays]]
deps = ["LinearAlgebra", "Random"]
uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
@@ -121,17 +133,25 @@ uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
deps = ["LinearAlgebra", "SparseArrays"]
uuid = "10745b16-79ce-11e8-11f9-7d13ad32a3b2"
-[[TOML]]
-deps = ["Dates"]
-uuid = "9d418dce-91a8-11e8-0173-7b01a971d501"
-
[[Test]]
deps = ["Distributed", "InteractiveUtils", "Logging", "Random"]
uuid = "8dfed614-e22c-5e08-85e1-65c5234f0b40"
[[UUIDs]]
-deps = ["Random"]
+deps = ["Random", "SHA"]
uuid = "cf7118a7-6976-5b1a-9a39-7adc72f591a4"
[[Unicode]]
uuid = "4ec0a83e-493e-50e2-b9ac-8f72acf5a8f5"
+
+[[VersionParsing]]
+deps = ["Compat"]
+git-tree-sha1 = "c9d5aa108588b978bd859554660c8a5c4f2f7669"
+uuid = "81def892-9a0e-5fdd-b105-ffc91e053289"
+version = "1.1.3"
+
+[[ZMQ]]
+deps = ["BinaryProvider", "FileWatching", "Libdl", "Sockets", "Test"]
+git-tree-sha1 = "34e7ac2d1d59d19d0e86bde99f1f02262bfa1613"
+uuid = "c2297ded-f4af-51ae-bb23-16f91089e4e1"
+version = "1.0.0"
diff --git a/Project.toml b/Project.toml
index ebae8eb..116ec28 100644
--- a/Project.toml
+++ b/Project.toml
@@ -3,7 +3,9 @@ uuid = "a2de2ff4-d7bb-11e8-2879-f9ef9fa2c94f"
version = "0.1.0"
[deps]
-JuliaAcademyData = "18b7da76-0988-5e3b-acac-6290be3a708f"
+Glob = "c27321d9-0574-5035-807b-f59d2c89b15c"
+IJulia = "7073ff75-c697-5162-941a-fcdaad2a7d2a"
+JSON = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
Literate = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
Pkg = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
 +#
+# This is trivial — and there are better ways to do this in the first place —
+# but the beauty of gradient descent is that it extends to much more complicated
+# examples. For example, we can even fit a differential equation with this method:
+#
+#
+#
+# This is trivial — and there are better ways to do this in the first place —
+# but the beauty of gradient descent is that it extends to much more complicated
+# examples. For example, we can even fit a differential equation with this method:
+#
+#  +#
+# But let's examine that line-fitting first as its simplicity makes a number of
+# points clear. To begin, let's load some data.
+
+using DifferentialEquations, CSV #src
+import Random #src
+Random.seed!(20) #src
+generate_data(ts) = solve(ODEProblem([1.0,1.0],(0.0,10.0),[1.5,1.0,3.0,1.0]) do du,u,p,t; du[1] = p[1]*u[1] - p[2]*prod(u); du[2] = -p[3]*u[2] + p[4]*prod(u); end, saveat=ts)[1,:].*(1.0.+0.02.*randn.()).+0.05.*randn.() #src
+ts = 0:.005:1 #src
+ys = generate_data(ts) #src
+CSV.write(datapath("data/020-descent-data.csv"), (t=ts, y=ys)) #src
+
+using CSV
+df = CSV.read(datapath("data/020-descent-data.csv"))
+#-
+using Plots
+scatter(df.t, df.y, xlabel="time", label="data")
+
+# Now we want to fit some model to this data — for a linear model we just need
+# two parameters:
+#
+# $$
+# y = m x + b
+# $$
+#
+# Lets create a structure that represents this:
+
+mutable struct LinearModel
+ m::Float64
+ b::Float64
+end
+(model::LinearModel)(x) = model.m*x + model.b
+
+# And create a randomly picked model to see how we do:
+linear = LinearModel(randn(), randn())
+plot!(df.t, linear.(df.t), label="model")
+
+# Of course, we just chose our `m` and `b` at random here, of course it's not
+# going to fit our data well! Let's quantify how far we are from an ideal line
+# with a _loss_ function:
+
+loss(f, xs, ys) = sum((f.(xs) .- ys).^2)
+loss(linear, df.t, df.y)
+
+# That's a pretty big number — and we want to decrease it. Let's update our plot
+# to include this loss value in the legend so we can keep track:
+
+p = scatter(df.t, df.y, xlabel="time", label="data")
+plot!(p, df.t, linear.(df.t), label="model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# And now we want to try to improve the fit. To do so, we just need to make
+# the loss function as small as possible. We can of course simply try a bunch
+# of values and brute-force a "good" solution. Plotting this as a three-dimensional
+# surface gives us the imagery of a hill, and our goal is to find our way to the bottom:
+
+ms, bs = (-1:.01:6, -2:.05:2.5)
+surface(ms, bs, [loss(LinearModel(m, b), df.t, df.y) for b in bs for m in ms], xlabel="m values", ylabel="b values", title="loss value")
+
+# A countour plot makes it a bit more obvious where the minimum is:
+
+contour(ms, bs, [loss(LinearModel(m, b), df.t, df.y) for b in bs for m in ms], levels=150, xlabel="m values", ylabel="b values")
+
+# But building those graphs are expensive! And it becomes completely intractible as soon as we
+# have more than a few parameters to fit. We can instead just try nudging the
+# current model's values to simply figure out which direction is "downhill":
+
+linear.m += 0.1
+plot!(p, df.t, linear.(df.t), label="new model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# We'll either have made things better or worse — but either way it's easy to
+# see which way to change `m` in order to improve our model.
+#
+# Essentially, what we're doing here is we're finding the derivative of our
+# loss function with respect to `m`, but again, there's a bit to be desired
+# here. Instead of evaluating the loss function twice and observing the difference,
+# we can just ask Julia for the derivative! This is the heart of differentiable
+# programming — the ability to ask a _complete program_ for its derivative.
+#
+# There are several techniques that you can use to compute the derivative. We'll
+# use the [Zygote package](https://fluxml.ai/Zygote.jl/latest/) first. It will
+# take a second as it compiles the "adjoint" code to compute the derivatives.
+# Since we're doing this in multiple dimensions, the two derivatives together
+# are called the gradient:
+
+using Zygote
+grads = Zygote.gradient(linear) do m
+ return loss(m, df.t, df.y)
+end
+grads
+
+# So there we go! Zygote saw that the model was gave it — `linear` — had two fields and thus
+# it computed the derivative of the loss function with respect to those two
+# parameters.
+#
+# Now we know the slope of our loss function — and thus
+# we know which way to move each parameter to improve it! We just need to iteratively walk
+# downhill! We don't want to take too large a step, so we'll multiply each
+# derivative by a "learning rate," typically called `η`.
+η = 0.001
+linear.m -= η*grads[1][].m
+linear.b -= η*grads[1][].b
+
+plot!(p, df.t, linear.(df.t), label="updated model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# Now we just need to do this a bunch of times!
+
+for i in 1:200
+ grads = Zygote.gradient(linear) do m
+ return loss(m, df.t, df.y)
+ end
+ linear.m -= η*grads[1][].m
+ linear.b -= η*grads[1][].b
+ i > 40 && i % 10 != 1 && continue
+#nb IJulia.clear_output(true)
+ scatter(df.t, df.y, label="data", xlabel="time", legend=:topleft)
+ display(plot!(df.t, linear.(df.t), label="model (loss: $(round(loss(linear, df.t, df.y), digits=3)))"))
+end
+
+#src === CREATING GIF ===
+f = let #src
+ linear = LinearModel(randn(), randn()) #src
+ f = @gif for i in 1:150 #src
+ grads = Zygote.gradient(linear) do m #src
+ return loss(m, df.t, df.y) #src
+ end #src
+ linear.m -= η*grads[1][].m #src
+ linear.b -= η*grads[1][].b #src
+ scatter(df.t, df.y, label="data", xlabel="time", legend=:topleft) #src
+ plot!(df.t, linear.(df.t), label="model (loss: $(round(loss(linear, df.t, df.y), digits=3)))") #src
+ end #src
+ mv(f.filename, datapath("images/020-linear.gif")) #src
+end #src
+
+
+
+# That's looking pretty good now! You might be saying this is crazy — I know
+# how to do a least squares fit! And you'd be right — in this case you can
+# easily do this with a linear solve of the system of equations:
+m, b = [df.t ones(size(df.t))] \ df.y
+
+@show (m, b)
+@show (linear.m, linear.b);
+
+# ## Exercise: Use gradient descent to fit a quadratic model to the data
+#
+# Obviously a linear fit leaves a bit to be desired here. Try to use the same
+# framework to fit a quadratic model. Check your answer against the algebraic
+# solution with the `\` operator.
+
+struct PolyModel
+ p::Vector{Float64}
+end
+function (m::PolyModel)(x)
+ r = m.p[1]*x^0
+ for i in 2:length(m.p)
+ r += m.p[i]*x^(i-1)
+ end
+ return r
+end
+poly = PolyModel(rand(3))
+loss(poly, df.t, df.y)
+η = 0.001
+for i in 1:1000
+ grads = Zygote.gradient(poly) do m
+ return loss(m, df.t, df.y)
+ end
+ poly.p .-= η.*grads[1].p
+end
+scatter(df.t, df.y, label="data", legend=:topleft)
+plot!(df.t, poly.(df.t), label="model by descent")
+plot!(df.t, PolyModel([df.t.^0 df.t df.t.^2] \ df.y).(df.t), label="model by linear solve")
+
+# ## Nonlinearities
+#
+# Let's see what happens when load a bit more data:
+
+let #src
+ ts = 0:.04:8 #src
+ ys = generate_data(ts) #src
+ CSV.write(datapath("data/020-descent-data-2.csv"), (t=ts, y=ys)) #src
+end #src
+df2 = CSV.read(datapath("data/020-descent-data-2.csv"))
+scatter(df2.t, df2.y, xlabel="t", label="more data")
+
+# Now what? This clearly won't be fit well with a low-order polynomial, and
+# even a high-order polynomial will get things wrong once we try to see what
+# will happen in the "future"!
+#
+# Let's use a bit of knowledge about where this data comes from: these happen
+# to be the number of rabbits in a predator-prey system! We can express the
+# general behavior with a pair of differential equations:
+#
+# $$
+# x' = \alpha x - \beta x y \\
+# y' = -\delta y + \gamma x y
+# $$
+#
+# * $x$ is the number of rabbits (🐰)
+# * $y$ is the number of wolves (🐺)
+# * $\alpha$ and $\beta$ describe the growth and death rates for the rabbits
+# * $\gamma$ and $\delta$ describe the growth and death rates for the wolves
+#
+# But we don't know what those rate constants are — all we have is the population
+# of rabbits over time.
+#
+# These are the classic Lotka-Volterra equations, and can be expressed in Julia
+# using the [DifferentialEquations](https://github.com/JuliaDiffEq/DifferentialEquations.jl) package:
+using DifferentialEquations
+function rabbit_wolf(du,u,p,t)
+ 🐰, 🐺 = u
+ α, β, δ, γ = p
+ du[1] = α*🐰 - β*🐰*🐺
+ du[2] = -δ*🐺 + γ*🐰*🐺
+end
+u0 = [1.0,1.0]
+tspan = extrema(df2.t)
+p = rand(4).+1 # We don't know what this is!
+## But lets see what the model looks like right now:
+prob = ODEProblem(rabbit_wolf,u0,tspan,p)
+sol = solve(prob, Tsit5(), saveat=df2.t)
+
+scatter(df2.t, df2.y, xlabel="t", label="more data")
+plot!(sol, label=["rabbits","wolves"])
+
+# So we're going to have to improve this — unlike the previous examples, we don't
+# have an easy algebraic solution here! But let's try using gradient descent.
+# The easiest way to get gradients out of a differential equation solver right
+# now is through the [DiffEqFlux package](https://github.com/JuliaDiffEq/DiffEqFlux.jl), and instead of manually converging,
+# we can use the Flux package to automatically (and more smartly) handle the gradient descent. Just
+# like before, though, we compute the loss of the model evaluation — and in this
+# case the model is _solving a differential equation!_
+using Flux, DiffEqFlux
+p = Flux.param(ones(4))
+diffeq_loss(p, xs, ys) = sum(abs2, diffeq_rd(p,prob,Tsit5(),saveat=df2.t)[1,:] .- df2.y)
+
+# This works slightly differently — we now track the gradients directly in the
+# p vector:
+p.grad
+#-
+l = diffeq_loss(p, df2.t, df2.y)
+#-
+DiffEqFlux.Tracker.back!(l) # we need to back-propagate our tracking of the gradients
+p.grad # but now we can see the gradients involved in that computation!
+
+# So now we can do exactly the same thing as before: iteratively update the parameters
+# to descend to a (hopefully) well-fit model:
+#
+# ```julia
+# p.data .-= η*p.grad
+# ```
+#
+# But we can be a bit smarter about this just by asking Flux to handle everything
+# with its train! function and associated functionality:
+
+data = Iterators.repeated((df2.t, df2.y), 150)
+opt = ADAM(0.1)
+history = Any[] #src
+cb = function () #callback function to observe training
+#nb IJulia.clear_output(true)
+ plt = scatter(df2.t, df2.y, label="data", ylabel="population (thousands)", xlabel="t")
+ display(plot!(plt, solve(remake(prob,p=Flux.data(p)),Tsit5(),saveat=0.1),
+ ylim=(0,8), label=["rabbits","wolves"], title="loss: $(round(Flux.data(diffeq_loss(p, df2.t, df2.y)), digits=3))"))
+ push!(history, plt) #src
+end
+Flux.train!((xs, ys)->diffeq_loss(p, xs, ys), [p], data, opt, cb = cb)
+
+f = @gif for i in 1:length(history) #src
+ plot(history[i]) #src
+end #src
+mv(f.filename, datapath("images/020-diffeq.gif")) #src
+
+# # Summary
+#
+# You can now see the power of differentiating whole programs — we can easily
+# and efficiently tune parameters without brute forcing solutions. Gradient
+# descent easily extends to machine learning and artificial intelligence
+# applications — and there are a number of tricks that can increase its efficiency
+# and help avoid local minima. There are a variety of other places where knowing the gradient can
+# be powerful and helpful.
diff --git a/Courses/Differentiable Programming/030 Neural Differential Equations.jl b/Courses/Differentiable Programming/030 Neural Differential Equations.jl
new file mode 100644
index 0000000..0b0f013
--- /dev/null
+++ b/Courses/Differentiable Programming/030 Neural Differential Equations.jl
@@ -0,0 +1,86 @@
+using Flux, DiffEqFlux, StochasticDiffEq, Plots, DiffEqMonteCarlo
+
+u0 = Float32[2.; 0.]
+datasize = 30
+tspan = (0.0f0,1.0f0)
+
+function trueODEfunc(du,u,p,t)
+ true_A = [-0.1 2.0; -2.0 -0.1]
+ du .= ((u.^3)'true_A)'
+end
+t = range(tspan[1],tspan[2],length=datasize)
+mp = Float32[0.2,0.2]
+function true_noise_func(du,u,p,t)
+ du .= mp.*u
+end
+prob = SDEProblem(trueODEfunc,true_noise_func,u0,tspan)
+
+# Take a typical sample from the mean
+monte_prob = MonteCarloProblem(prob)
+monte_sol = solve(monte_prob,SOSRI(),num_monte = 100)
+monte_sum = MonteCarloSummary(monte_sol)
+sde_data = Array(timeseries_point_mean(monte_sol,t))
+
+dudt = Chain(x -> x.^3,
+ Dense(2,50,tanh),
+ Dense(50,2))
+ps = Flux.params(dudt)
+n_sde = x->neural_dmsde(dudt,x,mp,tspan,SOSRI(),saveat=t,reltol=1e-1,abstol=1e-1)
+
+pred = n_sde(u0) # Get the prediction using the correct initial condition
+
+dudt_(u,p,t) = Flux.data(dudt(u))
+g(u,p,t) = mp.*u
+nprob = SDEProblem(dudt_,g,u0,(0.0f0,1.2f0),nothing)
+
+monte_nprob = MonteCarloProblem(nprob)
+monte_nsol = solve(monte_nprob,SOSRI(),num_monte = 100)
+monte_nsum = MonteCarloSummary(monte_nsol)
+#plot(monte_nsol,color=1,alpha=0.3)
+p1 = plot(monte_nsum, title = "Neural SDE: Before Training")
+scatter!(p1,t,sde_data',lw=3)
+
+scatter(t,sde_data[1,:],label="data")
+scatter!(t,Flux.data(pred[1,:]),label="prediction")
+
+function predict_n_sde()
+ n_sde(u0)
+end
+loss_n_sde1() = sum(abs2,sde_data .- predict_n_sde())
+loss_n_sde10() = sum([sum(abs2,sde_data .- predict_n_sde()) for i in 1:10])
+Flux.back!(loss_n_sde1())
+
+data = Iterators.repeated((), 10)
+opt = ADAM(0.025)
+cb = function () #callback function to observe training
+ sample = predict_n_sde()
+ # loss against current data
+ display(sum(abs2,sde_data .- sample))
+ # plot current prediction against data
+ cur_pred = Flux.data(sample)
+ pl = scatter(t,sde_data[1,:],label="data")
+ scatter!(pl,t,cur_pred[1,:],label="prediction")
+ display(plot(pl))
+end
+
+# Display the SDE with the initial parameter values.
+cb()
+
+Flux.train!(loss_n_sde1 , ps, Iterators.repeated((), 100), opt, cb = cb)
+Flux.train!(loss_n_sde10, ps, Iterators.repeated((), 20), opt, cb = cb)
+
+dudt_(u,p,t) = Flux.data(dudt(u))
+g(u,p,t) = mp.*u
+nprob = SDEProblem(dudt_,g,u0,(0.0f0,1.2f0),nothing)
+
+monte_nprob = MonteCarloProblem(nprob)
+monte_nsol = solve(monte_nprob,SOSRI(),num_monte = 100)
+monte_nsum = MonteCarloSummary(monte_nsol)
+#plot(monte_nsol,color=1,alpha=0.3)
+p2 = plot(monte_nsum, title = "Neural SDE: After Training", xlabel="Time")
+scatter!(p2,t,sde_data',lw=3,label=["x" "y" "z" "y"])
+
+plot(p1,p2,layout=(2,1))
+
+savefig("neural_sde.pdf")
+savefig("neural_sde.png")
diff --git a/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl b/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl
new file mode 100644
index 0000000..6cc7a7f
--- /dev/null
+++ b/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl
@@ -0,0 +1,260 @@
+# # How To Aim Your Flagon
+
+#-
+
+# ## Loading your Trebuchet
+
+#-
+
+# Today we practice the ancient medieval art of throwing stuff. First up, we load our trebuchet simulator, Trebuchet.jl.
+
+using Trebuchet
+
+# We can see what the trebuchet looks like, by explicitly creating a trebuchet state, running a simulation, and visualising the trajectory.
+
+t = TrebuchetState()
+simulate(t)
+visualise(t)
+
+# For training and optimisation, we don't need the whole visualisation, just a simple function that accepts and produces numbers. The `shoot` function just takes a wind speed, angle of release and counterweight mass, and tells us how far the projectile got.
+
+function shoot((wind, angle, weight))
+ Trebuchet.shoot((wind, Trebuchet.deg2rad(angle), weight))[2]
+end
+
+#-
+
+shoot([0, 45, 400])
+
+# It's worth playing with these parameters to see the impact they have. How far can you throw the projectile, tweaking only the angle of release?
+
+shoot([0, 40, 400])
+
+#-
+
+# There's actually a much better way of aiming the trebuchet. Let's load up a machine learning library, Flux, and see what we can do.
+
+using Flux, Trebuchet
+using Flux.Tracker: gradient, forwarddiff
+
+# Firstly, we're going to wrap `shoot` to take a _parameter vector_ (just a list of the three numbers we're interested in). There's also a call to `forwarddiff` here, which tells Flux to differentiate the trebuchet itself using forward mode. The number of parameters is small, so forward mode will be the most efficient way to do it. Otherwise Flux defaults to reverse mode.
+
+shoot(ps) = forwarddiff(p->shoot(p...), ps)
+
+# We can get a distance as usual.
+
+shoot([0, 45, 200])
+
+# But we can also get something much more interesting: *gradients* for each of those parameters with respect to distance.
+
+gradient(x->forwarddiff(shoot, x), [0.0, 45, 200])
+
+# What does these numbers mean? The gradient tells us, very roughly, that if we increase a parameter – let's say we make wind speed 1 m/s stronger – distance will also increase by about 4 metres. Let's try that.
+Zygote.gradient(x->forwarddiff(shoot, x), [0.0, 45, 200])
+
+shoot([1, 45, 200])
+
+# Lo and behold, this is indeed about four metres further!
+
+shoot([1, 45, 200]) - shoot([0, 45, 200])
+
+# So this seems like very useful information if we're trying to aim, or maximise distance. Notice that our gradient for the release angle is negative – increasing angle will decrease distance, so in other words we should probably *decrease* angle if we want more distance. Let's try that.
+
+shoot([0, 10, 200])
+
+# Oh no, this is actually *less* far than before!
+
+#-
+
+# So if the angle is too shallow, the projectile doesn't spend enough time in the air to gain any distance before hitting the ground. But if it's too high, the projectile doesn't have enough horizontal speed even with lots of time in the air. So we'll have to find a middle ground.
+#
+# More generally, the lesson here is that the gradient only gives you limited information; it helps us take a small step towards a better aim, and we can keep iterating to get to the best possible aim. For example, we choose a starting angle:
+
+angle = 45
+shoot([0, angle, 200])
+
+# Get a gradient for `angle` alone:
+
+dangle = gradient(angle -> shoot(Tracker.collect([0, angle, 200])), angle)[1] |> Flux.data
+
+# Update the angle, using the learning rate η:
+
+η = 10
+angle += η*dangle
+
+#-
+
+shoot([0, angle, 200])
+
+# Now we just lather, rinse and repeat! Ok, maybe we should write a loop to automate this a bit.
+
+for i = 1:10
+ dangle = gradient(angle -> shoot(Tracker.collect([0, angle, 200])), angle)[1] |> Flux.data
+ angle += η*dangle
+ @show angle
+end
+shoot([0, angle, 200])
+
+# Notice how the change in the angle slows down as things converge. Turns out the best angle is about 30 degrees, and we can hit about 90 metres.
+#
+# We can make this nicely repeatable and get the best angle for any given wind speed.
+
+function best_angle(wind)
+ angle = 45
+ objective(angle) = shoot(Tracker.collect([wind, angle, 200]))
+ for i = 1:10
+ dangle = gradient(objective, angle)[1] |> Flux.data
+ angle += η*dangle
+ end
+ return angle
+end
+
+#-
+
+best_angle(0)
+
+#-
+
+best_angle(10)
+
+#-
+
+best_angle(-10)
+
+# It turns out that if the wind is on our side, we should just throw the projectile upwards and let it get blown along. If the wind is strong against us, just chuck that stone right into it.
+
+t = TrebuchetState(release_angle = deg2rad(19), wind_speed = -10)
+simulate(t)
+visualise(t)
+
+# ## Accuracy Matters
+
+#-
+
+# In optimisation terms, we just created an objective (distance) and tried to maximise that objective. Flinging boulders as far as possible has its moments, but lacks a certain subtlety. What if we instead want to hit a precise target?
+
+t = TrebuchetState()
+simulate(t)
+visualise(t, 50)
+
+# The way to do this is to state the problem in terms of maximising, or minisming, some number – the objective. In this case, an easy way to come up with an objective is to take the difference from our target (gets closer to 0 as aim gets better) and square it (so it's always positive: 0 is the lowest *and* best possible score).
+
+#-
+
+# Here's a modified `best_angle` function that takes a target and tells us the distance it acheived.
+
+η = 0.1
+function best_angle(wind, target)
+ angle = 45
+ objective(angle) = (shoot(Tracker.collect([wind, angle, 200])) - target)^2
+ for i = 1:30
+ dangle = gradient(objective, angle)[1] |> Flux.data
+ angle -= η*dangle
+ end
+ return angle, shoot([wind, angle, 200])
+end
+
+# It's pretty accurate!
+
+best_angle(0, 50)
+
+# Even when we try to push it, by making wind really strong.
+
+best_angle(-20, 35)
+
+#-
+
+t = TrebuchetState(release_angle = deg2rad(21.8), weight = 200, wind_speed = -20)
+simulate(t)
+visualise(t, 35)
+
+# ## Siege Weapon Autopilot
+
+#-
+
+# Finally, we go one level more meta by training a neural network to aim the trebuchet for us. Rather than solving a whole optimisation problem every time we want to aim, we can just ask the network for good parameters and get them in constant time.
+#
+# Here's a simple multi layer perceptron. Its input is two parameters (wind speed and target) and its output is two more (release angle and counterweight mass).
+
+model = Chain(Dense(2, 16, σ),
+ Dense(16, 64, σ),
+ Dense(64, 16, σ),
+ Dense(16, 2)) |> f64
+
+θ = params(model)
+
+function aim(wind, target)
+ angle, weight = model([wind, target])
+ angle = σ(angle)*90
+ weight = weight + 200
+ angle, weight
+end
+
+distance(wind, target) = shoot(Tracker.collect([wind, aim(wind, target)...]))
+
+# The model's initial guesses will be fairly random, and miss the mark.
+
+aim(0, 70)
+
+#-
+
+distance(0, 70)
+
+# However, just as before, we can define an objective – or loss – and get gradients.
+
+function loss(wind, target)
+ try
+ (distance(wind, target) - target)^2
+ catch e
+ # Roots.jl sometimes give convergence errors, ignore them
+ param(0)
+ end
+end
+
+loss(0, 70)
+
+# This time, though, we'll get gradients for the *model parameters*, and updating these will improve the network's accuracy. This works because we're able to differentiate the *whole program*; the backwards pass propagates errors through the trebuchet simulator and then through the ML model.
+
+dθ = gradient(θ) do
+ loss(0, 70)
+end
+dθ[model[1].W]
+
+#-
+
+DIST = (20, 100) # Maximum target distance
+SPEED = 5 # Maximum wind speed
+
+lerp(x, lo, hi) = x*(hi-lo)+lo
+
+randtarget() = (randn() * SPEED, lerp(rand(), DIST...))
+
+#-
+
+using Statistics
+
+meanloss() = mean(sqrt(loss(randtarget()...)) for i = 1:100)
+
+opt = ADAM()
+
+dataset = (randtarget() for i = 1:10_000)
+
+Flux.train!(loss, θ, dataset, opt, cb = Flux.throttle(() -> @show(meanloss()), 10))
+
+# After only a few minutes of training, we're getting solid accuracy, even on hard wind speeds and targets. You can run the training loop again to improve the accuracy even further.
+
+wind, target = -10, 50
+angle, mass = Flux.data.(aim(wind, target))
+t = TrebuchetState(release_angle = deg2rad(angle), weight = mass, wind_speed = wind)
+simulate(t)
+visualise(t, target)
+
+# Notice that aiming with a neural net in one shot is significantly faster than solving the optimisation problem; and we only have a small loss in accuracy.
+
+@time aim(wind, target)
+
+#-
+
+@time best_angle(wind, target)
+
+#-
diff --git a/Courses/Differentiable Programming/050 Forward Differentiation.jl b/Courses/Differentiable Programming/050 Forward Differentiation.jl
new file mode 100644
index 0000000..fdc0453
--- /dev/null
+++ b/Courses/Differentiable Programming/050 Forward Differentiation.jl
@@ -0,0 +1,325 @@
+module ADPackages #src
+# Some settings for running this interactively #src
+interactive_use = false #src
+plotting_off = false #src
+using BenchmarkTools #src
+if interactive_use #src
+BenchmarkTools.DEFAULT_PARAMETERS.seconds = 0.1 #src
+end #src
+
+# # Using AD packages
+#
+# While a theoretical understanding behind how automatic differentiation work
+# is interesting, in practice, being able to use existing AD packages might
+# be good enough so this is where we will start.
+# Julia has many excellent packages for AD. The purpose of this lecture
+# for you to try a few of them out and apply them to real problems like solving
+# optimization problems using AD.
+
+# ## ForwardDiff
+#
+# The most popular package for AD in Julia is [`ForwardDiff`](https://github.com/JuliaDiff/ForwardDiff.jl).
+# It uses something called *forward mode automatic differentiation* using "Dual numbers"
+# and operator overloading. Forward mode AD is efficient if the function
+# being differentiated is $\mathbb{R}^N -> \mathbb{R}^M$ with $N <= M$. In other words,
+# the dimension of the input argument should be equal or greater than the number of
+# output arguments.
+# Foroward mode AD is however not so efficient for example when `M = 1` and `N` is big, which is common in
+# e.g. machine learning. In these cases *reverse mode automatic differentiation* is
+# more efficient, and we will look at that later.
+
+# ### Derivative of scalar functions
+#
+# To have a function to start experimenting with, we define the (scalar to
+# scalar) function `f(x)` and its analytical derivative
+# `fp(x)`
+
+f(x) = exp(x) / (sin(x)^3 + cos(x)^3);
+fp(x) = exp(x) * (3sin(x) + sin(3x) + 2cos(3x)) / 2(sin(x)^3 + cos(x)^3)^2;
+
+# We can visualize the function and the derivative (here using the Plots.jl package)
+if !plotting_off #src
+using Plots
+end #src
+xs = 0.0:0.01:1.4
+if !plotting_off #src
+plot(xs, [f.(xs), fp.(xs)]; labels = ["f" "fp"])
+end #src
+
+# The only thing to do to differentiate this function using AD is to import `ForwardDiff`
+# and call the `ForwardDiff.derivative` function with the function we want to differentiate and
+# at what point we want the derivative. The function should take a scalar as an argument
+# and return a scalar and that is what our function `f` above does.
+
+import ForwardDiff
+ad_derivative = ForwardDiff.derivative(f, pi/4)
+analytical_derivative = fp(pi/4)
+@assert ad_derivative ≈ analytical_derivative #src
+@show ad_derivative - analytical_derivative;
+
+# We can see that the AD derivative is "exact" (at least exact in the sense of floating
+# point precision) to the analytical ones.
+
+# #### Performance
+#
+# It can be interesting to see what the performance of using AD vs the the performance of the
+# analytical derivative. We can use the benchmark framework [`BenchmarkTools.jl`](https://github.com/JuliaCI/BenchmarkTools.jl)
+# to help us make accurate benchmarks even for functions that execute very quickly.
+
+using BenchmarkTools
+
+@assert VERSION < v"1.1" "revise benchmarking for 1.1" #src
+
+############################################################ #src
+# TODO: THIS IS ONLY TRUE ON MASTER, THE OPTIMIZATION DOES NOT HAPPEN ON JULIA 1.0.1 #src
+# If we do some napkin math, we can see that the reported time here is completely bogus! #src
+# Making the not too terrible assumption that a CPU can do one operation per clockcycle and that #src
+# the CPU you are using has approximately 3 GHz then one instruction should take ~0.3 ns which is #src
+# much longer than the reported time here. And computing this derivative need to compute `sin`, `cos` #src
+# etc which take many CPU instructions. #src
+# We have now encounted one of hard problems when benchmarking, to make sure that the computer is actually #src
+# computing the things you want it to. What happens here is that the Julia compiler is able #src
+# to figure out that the input we gave the function (`pi/4`) is a constant and the optimizer #src
+# then figures out the result during compile time. We can see this as follows: #src
+# #src
+#g() = ForwardDiff.derivative(f, pi/4) #src
+# #src
+## Looking at the generated code for #src
+# #src
+#@code_llvm g() #src
+# #src
+# We can see that the function has been optimized to just return a single value. #src
+# The exact value looks a bit odd because it is written #src
+# but reinterpreting it as a Float64 value we can see that it is just the same #src
+# derivative as was returned from ForwardDiff: #src
+# #src
+#@show reinterpret(Float64, 0x4008D06AE62ADC94) #src
+# #src
+#@show ForwardDiff.derivative(f, pi/4) #src
+# #src
+# One way we can trick the optimizer (at least with the current version of it) to not optimized #src
+# away the computation #src
+# is to encapsulate our value in a container like a [`Ref`](https://docs.julialang.org/en/v1/base/c/#Core.Ref) #src
+# #src
+##################################################################################### #src
+
+# A function can be benchmarked by prepending the call with `@btime`.
+# This will run the function multiple time and collect statistics on the
+# time it took to execute the function:
+
+println("Original function")
+@btime f(pi/4);
+println("AD derivative")
+@btime ForwardDiff.derivative(f, pi/4);
+println("Analytical derivative")
+@btime fp(pi/4);
+
+# We can here see that for the way we implemented the analytical derivative there is virtually no
+# performance difference between the AD version and the analyitical version.
+# However, it should be noted that the current version of the analytical function is not the
+# one with the best performance. Feel free to try to improve it.
+
+# A nice thing about AD is that you don't have to spend time making sure that
+# not only is the derivative correct, but that it is also efficiently computed.
+# By using AD, you get "free" performance for the derivative by optimizing the function itself.
+
+# #### Second derivatives
+#
+# For scalar functions `ForwardDiff` does not come with built in functionality for computing
+# the second derivative. It is, fortunately, very easy to create such a function ourselves.
+# The second derivative is just the derivative of the derivative which we can implement as:
+
+derivative2(f, x) = ForwardDiff.derivative(z -> ForwardDiff.derivative(f, z), x)
+
+@assert derivative2(f, pi/4) ≈ -6.203532787672101 #src
+@show derivative2(f, pi/4);
+
+# Here, we created an anonymous function that computes derivatives of `f`,
+# `z -> ForwardDiff.derivative(f, z)`, and then we used that as the input
+# derivative for another `ForwardDiff.derivative` call. The derivative
+# of the derivative gives the second derivative. Simple!
+# Feel free to compute the second derivative by hand and verify that the result
+# is correct (and appreciate that AD savees you from doing it in the first place).
+# The correct analytical result is `-2sqrt(2) * exp(pi/4)`.
+
+# #### Differentiating functions with parameters
+#
+# It is common to have a function that depends on some parameters that are considered
+# fixed in the context of differentiation.
+# An example of this might be the function `g` (and its derivative `gp) below:
+
+g(x, a) = (x - a)^3
+gp(x, a) = 3*(x - a)^2
+
+# Here, `g` has the parameter `a` and we want to take the derivative with respect to `x`.
+# Recall that `ForwardDiff.derivative` needs a function that takes only one
+# argument, but `g` above takes two arguments, so it clearly cannot be used directly.
+# The solution is to create what is typically called a "closure", which is a new function
+# that "closes" over some parameter space.
+# For example, consider:
+
+const a = 3
+g2(x) = g(x, a)
+
+@show (2 - a)^3
+@show g2(2);
+
+# We now have a new function `g2` which takes only one argument (`x`) and "closes" over the
+# variable `a`. We can now differentiate `g2`.
+
+@show ForwardDiff.derivative(g2, 2.0)
+@show gp(2.0, 3);
+
+# It is possible to write this a bit more succintly using an anonymous function
+
+ForwardDiff.derivative(x -> g(x, a), 2.0)
+
+# ## Gradients
+#
+# If our function takes a vector as input and returns a scalar, the derivative
+# is a vector (called a gradient) which gives the sensitivity of the output with respect to
+# all inputs. A quite common function to use in examples involving optimization
+# is the [Rosenbrock function](https://en.wikipedia.org/wiki/Rosenbrock_function), defined as:
+
+function rosenbrock(x)
+ a = one(eltype(x))
+ b = 100 * a
+ result = zero(eltype(x))
+ for i in 1:length(x)-1
+ result += (a - x[i])^2 + b*(x[i+1] - x[i]^2)^2
+ end
+ return result
+end
+
+# Evaluating `rosenbrock` with a vector input indeed gives a scalar back.
+
+rosenbrock([1.0, 0.5, 2.0])
+@assert rosenbrock([1.0, 0.5, 2.0]) == 331.5 #src
+
+# We can see how this function looks by plotting it
+
+xs = -3:0.1:3
+ys = -3:0.1:3
+zs = [rosenbrock([x, y]) for x in xs, y in ys]
+if !plotting_off #src
+contour(xs, ys, zs; levels=40)
+end #src
+
+# Evaluating the `gradient` is almost as simple as the `derivative`:
+
+x_vec = [1.0, 2.0]
+ForwardDiff.gradient(rosenbrock, x_vec)
+
+# ### Performance
+#
+# When evaluating the gradient we are dealing with `Vector`s which require allocation
+# so there are a few extra performance considerations for `gradient` compared to `derivative`
+
+# #### Preallocating output
+#
+# `ForwardDiff.gradient` returns a `Vector` which needs to be allocated. We can preallocate
+# this so `ForwardDiff` doesn't need to to it by itself.
+
+z_vec = similar(x_vec)
+ForwardDiff.gradient!(z_vec, rosenbrock, x_vec)
+@show z_vec;
+
+# The result was now stored in the, by us, allocated `z_vec`. We can check the performance difference
+
+println("No preallocation")
+@btime ForwardDiff.gradient(rosenbrock, $x_vec)
+println("No preallocation")
+@btime ForwardDiff.gradient!($z_vec,rosenbrock, $x_vec)
+
+# We can see that we do one allocation less and that performance is significantly
+# improved.
+
+# #### Preallocating internal datastructures
+#
+# Even though we preallocated the output vector there are some
+# internal data structures used by ForwardDiff that we in addition can preallocate
+# This is done by creating a `GradientConfig`:
+
+gradient_cache = ForwardDiff.GradientConfig(rosenbrock, x_vec)
+@btime ForwardDiff.gradient!($z_vec, rosenbrock, $x_vec, $gradient_cache);
+
+# Which as we can see further increase performance.
+# All of this is documented in the ForwardDiff manual so the takehome message is
+# to read the manual of the package one uses. There are often valuable information
+# there that could (like in this case) significantly improve performance.
+
+# ### Solving optimization using ForwardDiff
+#
+# [`Optim`](https://github.com/JuliaNLSolvers/Optim.jl) is a package that has many useful optimization routines.
+# If you can provide the gradient (and even sec) you get access to optimization routines that can
+# have significantly better performance. Lets use first try to just optimize the function without
+# using any gradient information. This will default to using the
+# [Nelder-Mead method](https://en.wikipedia.org/wiki/Nelder%E2%80%93Mead_method).
+# We also stick a `@btime` in there to see how long time the optimization routine take.
+using Random; Random.seed!(1234) #src
+using Optim
+x0 = zeros(10)
+@btime optimize(rosenbrock, x0)
+
+# We can see that we require approximately 620 evaluations of `rosenbrock` before
+# a minimum was found. Let's try giving `Optim` the gradient as well:
+#
+using Random; Random.seed!(1234) #src
+const gradient_cache_optim = ForwardDiff.GradientConfig(rosenbrock, x0)
+const rosenbrock_gradient! = (z, x) -> ForwardDiff.gradient!(z,rosenbrock, x, gradient_cache_optim)
+
+@btime optimize(rosenbrock, rosenbrock_gradient!, x0)
+
+# Now we only called the function 92 times (and in addition the gradient 153 times)
+# Looking at the time taken this was almost a 3x speedup. The minimum we found had a
+# was also significantly smaller than when we used Nelder-Mead
+
+# ## Hessians
+# It is also possible to compute Hessians (second derivative) in a very similar way to `gradient`
+
+ForwardDiff.hessian(rosenbrock, [1.0, 2.0])
+
+# We leave out the details for `ForwardDiff.hessian` here and instead refer to the [`ForwardDiff.hessian`](http://www.juliadiff.org/ForwardDiff.jl/stable/user/api.html#Hessians-of-f(x::AbstractArray)::Real-1)
+# documentation.
+
+# ## Jacobians
+#
+# If our function takes a vector as argument and returns a vector, the derivative is a `Matrix` which
+# is known as the Jacobian. This derivative is useful when we want to solve a nonlinear system of
+# equations.
+# Let's consider the following function that slightly resembles the `rosenbrock` function:
+
+function rosenbrock_vector(x)
+ return [
+ 1 - x[1],
+ 10(x[2]-x[1]^2)
+ ]
+end
+
+# Indeed calling this function with a vector argument returns a vector:
+
+rosenbrock_vector([1.0, 0.5])
+
+# By now, we should be quite familiar with the ForwarDiff interface and you might
+# even guess how we should compute the Jacobian:
+
+ForwardDiff.jacobian(rosenbrock_vector, [1.0, 0.5])
+
+# The Jacobian functionality could be used for example in [`NLsolve.jl`](https://github.com/JuliaNLSolvers/NLsolve.jl),
+# which is a nonlinear equation solver.
+
+# ### Summary `ForwardDiff`
+# This should get you started with using `ForwardDiff`. If your functions do not have too big vectors as
+# input arguments, the performance should be good. It will likely not beat a carefully tuned
+# analytical implementaion of the derivative but it is oftan that from a productivity point of view
+# it is worth using AD.
+
+# ## Revisediff
+#
+# ForwardDiff is using what is known as forward mode differentiation.
+# If the number of input parameters is large and the output is just a scalar
+# then reverse mode differentation is likely more effective.
+#
+# TODO..
+
+end #src
diff --git a/Courses/Differentiable Programming/060 Reverse Differentiation.jl b/Courses/Differentiable Programming/060 Reverse Differentiation.jl
new file mode 100644
index 0000000..e69de29
diff --git a/Courses/Differentiable Programming/Manifest.toml b/Courses/Differentiable Programming/Manifest.toml
new file mode 100644
index 0000000..9b3c023
--- /dev/null
+++ b/Courses/Differentiable Programming/Manifest.toml
@@ -0,0 +1,872 @@
+# This file is machine-generated - editing it directly is not advised
+
+[[AbstractTrees]]
+deps = ["Markdown", "Test"]
+git-tree-sha1 = "6621d9645702c1c4e6970cc6a3eae440c768000b"
+uuid = "1520ce14-60c1-5f80-bbc7-55ef81b5835c"
+version = "0.2.1"
+
+[[Adapt]]
+deps = ["LinearAlgebra", "Test"]
+git-tree-sha1 = "53d8fec4f662088c1202530e338a11a919407f3b"
+uuid = "79e6a3ab-5dfb-504d-930d-738a2a938a0e"
+version = "0.4.2"
+
+[[Arpack]]
+deps = ["BinaryProvider", "Libdl", "LinearAlgebra"]
+git-tree-sha1 = "07a2c077bdd4b6d23a40342a8a108e2ee5e58ab6"
+uuid = "7d9fca2a-8960-54d3-9f78-7d1dccf2cb97"
+version = "0.3.1"
+
+[[ArrayInterface]]
+deps = ["Requires", "Test"]
+git-tree-sha1 = "6a1a371393e56f5e8d5657fe4da4b11aea0bfbae"
+uuid = "4fba245c-0d91-5ea0-9b3e-6abc04ee57a9"
+version = "0.1.1"
+
+[[AssetRegistry]]
+deps = ["Distributed", "JSON", "Pidfile", "SHA", "Test"]
+git-tree-sha1 = "b25e88db7944f98789130d7b503276bc34bc098e"
+uuid = "bf4720bc-e11a-5d0c-854e-bdca1663c893"
+version = "0.1.0"
+
+[[BandedMatrices]]
+deps = ["FillArrays", "LazyArrays", "LinearAlgebra", "MatrixFactorizations", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "dd74592d0952af59b97e12d6f69bfc9cc3a79614"
+uuid = "aae01518-5342-5314-be14-df237901396f"
+version = "0.9.2"
+
+[[Base64]]
+uuid = "2a0f44e3-6c83-55bd-87e4-b1978d98bd5f"
+
+[[BenchmarkTools]]
+deps = ["JSON", "Printf", "Statistics", "Test"]
+git-tree-sha1 = "5d1dd8577643ba9014574cd40d9c028cd5e4b85a"
+uuid = "6e4b80f9-dd63-53aa-95a3-0cdb28fa8baf"
+version = "0.4.2"
+
+[[BinDeps]]
+deps = ["Compat", "Libdl", "SHA", "URIParser"]
+git-tree-sha1 = "12093ca6cdd0ee547c39b1870e0c9c3f154d9ca9"
+uuid = "9e28174c-4ba2-5203-b857-d8d62c4213ee"
+version = "0.8.10"
+
+[[BinaryProvider]]
+deps = ["Libdl", "Logging", "SHA"]
+git-tree-sha1 = "8153fd64131cd00a79544bb23788877741f627bb"
+uuid = "b99e7846-7c00-51b0-8f62-c81ae34c0232"
+version = "0.5.5"
+
+[[BoundaryValueDiffEq]]
+deps = ["BandedMatrices", "DiffEqBase", "DiffEqDiffTools", "ForwardDiff", "LinearAlgebra", "NLsolve", "Reexport", "SparseArrays", "Test"]
+git-tree-sha1 = "0f4a4f86ae63671efd9b41de9dea8ad993f2daad"
+uuid = "764a87c0-6b3e-53db-9096-fe964310641d"
+version = "2.2.3"
+
+[[CSTParser]]
+deps = ["Tokenize"]
+git-tree-sha1 = "376a39f1862000442011390f1edf5e7f4dcc7142"
+uuid = "00ebfdb7-1f24-5e51-bd34-a7502290713f"
+version = "0.6.0"
+
+[[CSV]]
+deps = ["CategoricalArrays", "DataFrames", "Dates", "Mmap", "Parsers", "PooledArrays", "Profile", "Tables", "Unicode", "WeakRefStrings"]
+git-tree-sha1 = "078801ccf5a644df31cef99c9add46107b94aba5"
+uuid = "336ed68f-0bac-5ca0-87d4-7b16caf5d00b"
+version = "0.5.6"
+
+[[Calculus]]
+deps = ["Compat"]
+git-tree-sha1 = "f60954495a7afcee4136f78d1d60350abd37a409"
+uuid = "49dc2e85-a5d0-5ad3-a950-438e2897f1b9"
+version = "0.4.1"
+
+[[CategoricalArrays]]
+deps = ["Compat", "Future", "JSON", "Missings", "Printf", "Reexport"]
+git-tree-sha1 = "26601961df6afacdd16d67c1eec6cfe75e5ae9ab"
+uuid = "324d7699-5711-5eae-9e2f-1d82baa6b597"
+version = "0.5.4"
+
+[[CodecZlib]]
+deps = ["BinaryProvider", "Libdl", "Test", "TranscodingStreams"]
+git-tree-sha1 = "36bbf5374c661054d41410dc53ff752972583b9b"
+uuid = "944b1d66-785c-5afd-91f1-9de20f533193"
+version = "0.5.2"
+
+[[ColorTypes]]
+deps = ["FixedPointNumbers", "Random"]
+git-tree-sha1 = "10050a24b09e8e41b951e9976b109871ce98d965"
+uuid = "3da002f7-5984-5a60-b8a6-cbb66c0b333f"
+version = "0.8.0"
+
+[[Colors]]
+deps = ["ColorTypes", "FixedPointNumbers", "InteractiveUtils", "Printf", "Reexport", "Test"]
+git-tree-sha1 = "9f0a0210450acb91c730b730a994f8eef1d3d543"
+uuid = "5ae59095-9a9b-59fe-a467-6f913c188581"
+version = "0.9.5"
+
+[[CommonSubexpressions]]
+deps = ["Test"]
+git-tree-sha1 = "efdaf19ab11c7889334ca247ff4c9f7c322817b0"
+uuid = "bbf7d656-a473-5ed7-a52c-81e309532950"
+version = "0.2.0"
+
+[[Compat]]
+deps = ["Base64", "Dates", "DelimitedFiles", "Distributed", "InteractiveUtils", "LibGit2", "Libdl", "LinearAlgebra", "Markdown", "Mmap", "Pkg", "Printf", "REPL", "Random", "Serialization", "SharedArrays", "Sockets", "SparseArrays", "Statistics", "Test", "UUIDs", "Unicode"]
+git-tree-sha1 = "84aa74986c5b9b898b0d1acaf3258741ee64754f"
+uuid = "34da2185-b29b-5c13-b0c7-acf172513d20"
+version = "2.1.0"
+
+[[Contour]]
+deps = ["LinearAlgebra", "StaticArrays", "Test"]
+git-tree-sha1 = "b974e164358fea753ef853ce7bad97afec15bb80"
+uuid = "d38c429a-6771-53c6-b99e-75d170b6e991"
+version = "0.5.1"
+
+[[Crayons]]
+deps = ["Test"]
+git-tree-sha1 = "f621b8ef51fd2004c7cf157ea47f027fdeac5523"
+uuid = "a8cc5b0e-0ffa-5ad4-8c14-923d3ee1735f"
+version = "4.0.0"
+
+[[DataFrames]]
+deps = ["CategoricalArrays", "Compat", "IteratorInterfaceExtensions", "Missings", "PooledArrays", "Printf", "REPL", "Reexport", "SortingAlgorithms", "Statistics", "StatsBase", "TableTraits", "Tables", "Unicode"]
+git-tree-sha1 = "7c0f86a01be0f77cc7f3f9096ed875f1217487e1"
+uuid = "a93c6f00-e57d-5684-b7b6-d8193f3e46c0"
+version = "0.18.4"
+
+[[DataStructures]]
+deps = ["InteractiveUtils", "OrderedCollections", "Random", "Serialization", "Test"]
+git-tree-sha1 = "ca971f03e146cf144a9e2f2ce59674f5bf0e8038"
+uuid = "864edb3b-99cc-5e75-8d2d-829cb0a9cfe8"
+version = "0.15.0"
+
+[[DataValueInterfaces]]
+git-tree-sha1 = "bfc1187b79289637fa0ef6d4436ebdfe6905cbd6"
+uuid = "e2d170a0-9d28-54be-80f0-106bbe20a464"
+version = "1.0.0"
+
+[[Dates]]
+deps = ["Printf"]
+uuid = "ade2ca70-3891-5945-98fb-dc099432e06a"
+
+[[DelayDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "ForwardDiff", "MuladdMacro", "NLSolversBase", "OrdinaryDiffEq", "RecursiveArrayTools", "Reexport", "Roots"]
+git-tree-sha1 = "d933682653f8c3c922592d75e50b5a30689ede6d"
+uuid = "bcd4f6db-9728-5f36-b5f7-82caef46ccdb"
+version = "5.4.1"
+
+[[DelimitedFiles]]
+deps = ["Mmap"]
+uuid = "8bb1440f-4735-579b-a4ab-409b98df4dab"
+
+[[DiffEqBase]]
+deps = ["Compat", "Distributed", "DocStringExtensions", "FunctionWrappers", "IterativeSolvers", "IteratorInterfaceExtensions", "LinearAlgebra", "MuladdMacro", "Parameters", "RecipesBase", "RecursiveArrayTools", "RecursiveFactorization", "Requires", "Roots", "SparseArrays", "StaticArrays", "Statistics", "SuiteSparse", "TableTraits", "TreeViews"]
+git-tree-sha1 = "3c08441014d2e1bad515df5443dd2d0ba379888c"
+uuid = "2b5f629d-d688-5b77-993f-72d75c75574e"
+version = "5.12.0"
+
+[[DiffEqCallbacks]]
+deps = ["DataStructures", "DiffEqBase", "LinearAlgebra", "OrdinaryDiffEq", "RecipesBase", "RecursiveArrayTools", "StaticArrays", "Test"]
+git-tree-sha1 = "027a13f010f2a93b2df725b7f6202590ce6f559d"
+uuid = "459566f4-90b8-5000-8ac3-15dfb0a30def"
+version = "2.5.2"
+
+[[DiffEqDiffTools]]
+deps = ["LinearAlgebra", "SparseArrays", "StaticArrays"]
+git-tree-sha1 = "2d4f49c1839c1f30e4820400d8c109c6b16e869a"
+uuid = "01453d9d-ee7c-5054-8395-0335cb756afa"
+version = "0.13.0"
+
+[[DiffEqFinancial]]
+deps = ["DiffEqBase", "DiffEqNoiseProcess", "LinearAlgebra", "Markdown", "RandomNumbers", "Test"]
+git-tree-sha1 = "f250512b982b771f6bdb3df05b89df314f2c2580"
+uuid = "5a0ffddc-d203-54b0-88ba-2c03c0fc2e67"
+version = "2.1.0"
+
+[[DiffEqFlux]]
+deps = ["Adapt", "DiffEqBase", "DiffEqSensitivity", "DiffResults", "Flux", "ForwardDiff", "RecursiveArrayTools", "Requires"]
+git-tree-sha1 = "1c311e6a4f14c70c7ea33482db9856392c4b6b80"
+uuid = "aae7a2af-3d4f-5e19-a356-7da93b79d9d0"
+version = "0.5.0"
+
+[[DiffEqJump]]
+deps = ["Compat", "DataStructures", "DiffEqBase", "FunctionWrappers", "LinearAlgebra", "Parameters", "PoissonRandom", "Random", "RandomNumbers", "RecursiveArrayTools", "Statistics", "Test", "TreeViews"]
+git-tree-sha1 = "784b979eeca8e9586aea9e63edbdcf5573bf9449"
+uuid = "c894b116-72e5-5b58-be3c-e6d8d4ac2b12"
+version = "6.1.1"
+
+[[DiffEqMonteCarlo]]
+deps = ["DiffEqBase", "Distributed", "RecursiveArrayTools", "StaticArrays", "Statistics"]
+git-tree-sha1 = "edffd3e114b5c2cad15e7790db6d82f69e3f42ae"
+uuid = "78ddff82-25fc-5f2b-89aa-309469cbf16f"
+version = "0.15.1"
+
+[[DiffEqNoiseProcess]]
+deps = ["DataStructures", "DiffEqBase", "LinearAlgebra", "Random", "RandomNumbers", "RecipesBase", "RecursiveArrayTools", "Requires", "ResettableStacks", "StaticArrays", "Statistics"]
+git-tree-sha1 = "f5333c0aa6208680e48cd24ae6f759c262a1cf85"
+uuid = "77a26b50-5914-5dd7-bc55-306e6241c503"
+version = "3.3.1"
+
+[[DiffEqOperators]]
+deps = ["DiffEqBase", "ForwardDiff", "LinearAlgebra", "SparseArrays", "StaticArrays", "SuiteSparse"]
+git-tree-sha1 = "2884a79a72aac38347b247615ac42eda41aa36e0"
+uuid = "9fdde737-9c7f-55bf-ade8-46b3f136cc48"
+version = "3.5.0"
+
+[[DiffEqPhysics]]
+deps = ["Dates", "DiffEqBase", "DiffEqCallbacks", "ForwardDiff", "LinearAlgebra", "Printf", "Random", "RecipesBase", "RecursiveArrayTools", "Reexport", "StaticArrays", "Test"]
+git-tree-sha1 = "d3dbc53318a6477f496ae2347db98c3ded36c486"
+uuid = "055956cb-9e8b-5191-98cc-73ae4a59e68a"
+version = "3.1.0"
+
+[[DiffEqSensitivity]]
+deps = ["DataFrames", "DiffEqBase", "DiffEqCallbacks", "DiffEqDiffTools", "Flux", "ForwardDiff", "GLM", "LinearAlgebra", "QuadGK", "RecursiveArrayTools", "Statistics"]
+git-tree-sha1 = "09c964dc242f295180dd99d89fb2f259927029ef"
+uuid = "41bf760c-e81c-5289-8e54-58b1f1f8abe2"
+version = "3.2.4"
+
+[[DiffResults]]
+deps = ["Compat", "StaticArrays"]
+git-tree-sha1 = "34a4a1e8be7bc99bc9c611b895b5baf37a80584c"
+uuid = "163ba53b-c6d8-5494-b064-1a9d43ac40c5"
+version = "0.0.4"
+
+[[DiffRules]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "dc0869fb2f5b23466b32ea799bd82c76480167f7"
+uuid = "b552c78f-8df3-52c6-915a-8e097449b14b"
+version = "0.0.10"
+
+[[DifferentialEquations]]
+deps = ["BoundaryValueDiffEq", "DelayDiffEq", "DiffEqBase", "DiffEqCallbacks", "DiffEqFinancial", "DiffEqJump", "DiffEqMonteCarlo", "DiffEqNoiseProcess", "DiffEqPhysics", "DimensionalPlotRecipes", "LinearAlgebra", "MultiScaleArrays", "OrdinaryDiffEq", "Random", "RecursiveArrayTools", "Reexport", "SteadyStateDiffEq", "StochasticDiffEq", "Sundials"]
+git-tree-sha1 = "e5b3ca6afe2a064bdfecba483999ee75d81750c6"
+uuid = "0c46a032-eb83-5123-abaf-570d42b7fbaa"
+version = "6.4.0"
+
+[[DimensionalPlotRecipes]]
+deps = ["LinearAlgebra", "RecipesBase", "Test"]
+git-tree-sha1 = "d348688f9a3d02c24455327231c450c272b7401c"
+uuid = "c619ae07-58cd-5f6d-b883-8f17bd6a98f9"
+version = "0.2.0"
+
+[[Distances]]
+deps = ["LinearAlgebra", "Printf", "Random", "Statistics", "Test"]
+git-tree-sha1 = "a135c7c062023051953141da8437ed74f89d767a"
+uuid = "b4f34e82-e78d-54a5-968a-f98e89d6e8f7"
+version = "0.8.0"
+
+[[Distributed]]
+deps = ["Random", "Serialization", "Sockets"]
+uuid = "8ba89e20-285c-5b6f-9357-94700520ee1b"
+
+[[Distributions]]
+deps = ["LinearAlgebra", "PDMats", "Printf", "QuadGK", "Random", "SpecialFunctions", "Statistics", "StatsBase", "StatsFuns"]
+git-tree-sha1 = "56a158bc0abe4af5d4027af2275fde484261ca6d"
+uuid = "31c24e10-a181-5473-b8eb-7969acd0382f"
+version = "0.19.2"
+
+[[DocStringExtensions]]
+deps = ["LibGit2", "Markdown", "Pkg", "Test"]
+git-tree-sha1 = "0513f1a8991e9d83255e0140aace0d0fc4486600"
+uuid = "ffbed154-4ef7-542d-bbb7-c09d3a79fcae"
+version = "0.8.0"
+
+[[ExponentialUtilities]]
+deps = ["LinearAlgebra", "Printf", "SparseArrays"]
+git-tree-sha1 = "85e1ce16aa9b98793df704e17e7a0ceadefe404f"
+uuid = "d4d017d3-3776-5f7e-afef-a10c40355c18"
+version = "1.5.1"
+
+[[FileWatching]]
+uuid = "7b1f6079-737a-58dc-b8bc-7a2ca5c1b5ee"
+
+[[FillArrays]]
+deps = ["LinearAlgebra", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "9ab8f76758cbabba8d7f103c51dce7f73fcf8e92"
+uuid = "1a297f60-69ca-5386-bcde-b61e274b549b"
+version = "0.6.3"
+
+[[FixedPointNumbers]]
+git-tree-sha1 = "d14a6fa5890ea3a7e5dcab6811114f132fec2b4b"
+uuid = "53c48c17-4a7d-5ca2-90c5-79b7896eea93"
+version = "0.6.1"
+
+[[Flux]]
+deps = ["AbstractTrees", "Adapt", "CodecZlib", "Colors", "DelimitedFiles", "Juno", "LinearAlgebra", "MacroTools", "NNlib", "Pkg", "Printf", "Random", "Reexport", "Requires", "SHA", "Statistics", "StatsBase", "Tracker", "ZipFile"]
+git-tree-sha1 = "08212989c2856f95f90709ea5fd824bd27b34514"
+uuid = "587475ba-b771-5e3f-ad9e-33799f191a9c"
+version = "0.8.3"
+
+[[ForwardDiff]]
+deps = ["CommonSubexpressions", "DiffResults", "DiffRules", "InteractiveUtils", "LinearAlgebra", "NaNMath", "Random", "SparseArrays", "SpecialFunctions", "StaticArrays", "Test"]
+git-tree-sha1 = "4c4d727f1b7e0092134fabfab6396b8945c1ea5b"
+repo-rev = "master"
+repo-url = "https://github.com/JuliaDiff/ForwardDiff.jl.git"
+uuid = "f6369f11-7733-5829-9624-2563aa707210"
+version = "0.10.3+"
+
+[[FunctionWrappers]]
+deps = ["Compat"]
+git-tree-sha1 = "49bf793ebd37db5adaa7ac1eae96c2c97ec86db5"
+uuid = "069b7b12-0de2-55c6-9aab-29f3d0a68a2e"
+version = "1.0.0"
+
+[[FunctionalCollections]]
+deps = ["Test"]
+git-tree-sha1 = "04cb9cfaa6ba5311973994fe3496ddec19b6292a"
+uuid = "de31a74c-ac4f-5751-b3fd-e18cd04993ca"
+version = "0.5.0"
+
+[[Future]]
+deps = ["Random"]
+uuid = "9fa8497b-333b-5362-9e8d-4d0656e87820"
+
+[[GLM]]
+deps = ["Distributions", "LinearAlgebra", "Printf", "Random", "Reexport", "SparseArrays", "SpecialFunctions", "Statistics", "StatsBase", "StatsFuns", "StatsModels"]
+git-tree-sha1 = "bb918f52a8e2131857ddac319033610bb3be35a4"
+uuid = "38e38edf-8417-5370-95a0-9cbb8c7f171a"
+version = "1.3.0"
+
+[[GR]]
+deps = ["Base64", "DelimitedFiles", "LinearAlgebra", "Pkg", "Printf", "Random", "Serialization", "Sockets", "Test"]
+git-tree-sha1 = "9dff2d231311da78648abfa3287e3458a578d2f8"
+uuid = "28b8d3ca-fb5f-59d9-8090-bfdbd6d07a71"
+version = "0.40.0"
+
+[[GenericSVD]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "8aa93c3f3d81562a8962047eafcc5712af0a0f59"
+uuid = "01680d73-4ee2-5a08-a1aa-533608c188bb"
+version = "0.2.1"
+
+[[GeometryTypes]]
+deps = ["ColorTypes", "FixedPointNumbers", "IterTools", "LinearAlgebra", "StaticArrays"]
+git-tree-sha1 = "2b0bfb379a54bdfcd2942f388f7d045f8952373d"
+uuid = "4d00f742-c7ba-57c2-abde-4428a4b178cb"
+version = "0.7.5"
+
+[[HTTP]]
+deps = ["Base64", "Dates", "IniFile", "MbedTLS", "Sockets"]
+git-tree-sha1 = "6e59e7ec3c71eda9e0261c98896da5d3d008fa7d"
+uuid = "cd3eb016-35fb-5094-929b-558a96fad6f3"
+version = "0.8.3"
+
+[[IRTools]]
+deps = ["InteractiveUtils", "MacroTools", "Test"]
+git-tree-sha1 = "a9b1fc7745ae4745a634bbb6d1cb7fd64e37248a"
+uuid = "7869d1d1-7146-5819-86e3-90919afe41df"
+version = "0.2.2"
+
+[[IniFile]]
+deps = ["Test"]
+git-tree-sha1 = "098e4d2c533924c921f9f9847274f2ad89e018b8"
+uuid = "83e8ac13-25f8-5344-8a64-a9f2b223428f"
+version = "0.5.0"
+
+[[InteractiveUtils]]
+deps = ["Markdown"]
+uuid = "b77e0a4c-d291-57a0-90e8-8db25a27a240"
+
+[[IterTools]]
+deps = ["SparseArrays", "Test"]
+git-tree-sha1 = "79246285c43602384e6f1943b3554042a3712056"
+uuid = "c8e1da08-722c-5040-9ed9-7db0dc04731e"
+version = "1.1.1"
+
+[[IterativeSolvers]]
+deps = ["LinearAlgebra", "Printf", "Random", "RecipesBase", "SparseArrays", "Test"]
+git-tree-sha1 = "5687f68018b4f14c0da54d402bb23eecaec17f37"
+uuid = "42fd0dbc-a981-5370-80f2-aaf504508153"
+version = "0.8.1"
+
+[[IteratorInterfaceExtensions]]
+git-tree-sha1 = "a3f24677c21f5bbe9d2a714f95dcd58337fb2856"
+uuid = "82899510-4779-5014-852e-03e436cf321d"
+version = "1.0.0"
+
+[[JSExpr]]
+deps = ["JSON", "MacroTools", "Observables", "Test", "WebIO"]
+git-tree-sha1 = "013bc2143a2e84ea489365cf30db3407deb540c2"
+uuid = "97c1335a-c9c5-57fe-bc5d-ec35cebe8660"
+version = "0.5.0"
+
+[[JSON]]
+deps = ["Dates", "Distributed", "Mmap", "Sockets", "Test", "Unicode"]
+git-tree-sha1 = "1f7a25b53ec67f5e9422f1f551ee216503f4a0fa"
+uuid = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
+version = "0.20.0"
+
+[[Juno]]
+deps = ["Base64", "Logging", "Media", "Profile", "Test"]
+git-tree-sha1 = "4e4a8d43aa7ecec66cadaf311fbd1e5c9d7b9175"
+uuid = "e5e0dc1b-0480-54bc-9374-aad01c23163d"
+version = "0.7.0"
+
+[[LazyArrays]]
+deps = ["FillArrays", "LinearAlgebra", "MacroTools", "StaticArrays", "Test"]
+git-tree-sha1 = "5eec856c454496abe8f4504227fcc187205a502a"
+uuid = "5078a376-72f3-5289-bfd5-ec5146d43c02"
+version = "0.9.0"
+
+[[LibGit2]]
+uuid = "76f85450-5226-5b5a-8eaa-529ad045b433"
+
+[[Libdl]]
+uuid = "8f399da3-3557-5675-b5ff-fb832c97cbdb"
+
+[[LineSearches]]
+deps = ["LinearAlgebra", "NLSolversBase", "NaNMath", "Parameters", "Printf", "Test"]
+git-tree-sha1 = "54eb90e8dbe745d617c78dee1d6ae95c7f6f5779"
+uuid = "d3d80556-e9d4-5f37-9878-2ab0fcc64255"
+version = "7.0.1"
+
+[[LinearAlgebra]]
+deps = ["Libdl"]
+uuid = "37e2e46d-f89d-539d-b4ee-838fcccc9c8e"
+
+[[Literate]]
+deps = ["Base64", "JSON", "REPL", "Test"]
+git-tree-sha1 = "021e2e3106713e22a7f3769ebf9f2f4469670444"
+uuid = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
+version = "1.1.0"
+
+[[Logging]]
+uuid = "56ddb016-857b-54e1-b83d-db4d58db5568"
+
+[[MacroTools]]
+deps = ["CSTParser", "Compat", "DataStructures", "Test"]
+git-tree-sha1 = "daecd9e452f38297c686eba90dba2a6d5da52162"
+uuid = "1914dd2f-81c6-5fcd-8719-6d5c9610ff09"
+version = "0.5.0"
+
+[[Markdown]]
+deps = ["Base64"]
+uuid = "d6f4376e-aef5-505a-96c1-9c027394607a"
+
+[[MatrixFactorizations]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "cebc71d929a846dda61400f1cf3ba69c7e75fa63"
+uuid = "a3b82374-2e81-5b9e-98ce-41277c0e4c87"
+version = "0.0.4"
+
+[[MbedTLS]]
+deps = ["BinaryProvider", "Dates", "Libdl", "Random", "Sockets"]
+git-tree-sha1 = "85f5947b53c8cfd53ccfa3f4abae31faa22c2181"
+uuid = "739be429-bea8-5141-9913-cc70e7f3736d"
+version = "0.7.0"
+
+[[Measures]]
+deps = ["Test"]
+git-tree-sha1 = "ddfd6d13e330beacdde2c80de27c1c671945e7d9"
+uuid = "442fdcdd-2543-5da2-b0f3-8c86c306513e"
+version = "0.3.0"
+
+[[Media]]
+deps = ["MacroTools", "Test"]
+git-tree-sha1 = "75a54abd10709c01f1b86b84ec225d26e840ed58"
+uuid = "e89f7d12-3494-54d1-8411-f7d8b9ae1f27"
+version = "0.5.0"
+
+[[Missings]]
+deps = ["SparseArrays", "Test"]
+git-tree-sha1 = "f0719736664b4358aa9ec173077d4285775f8007"
+uuid = "e1d29d7a-bbdc-5cf2-9ac0-f12de2c33e28"
+version = "0.4.1"
+
+[[Mmap]]
+uuid = "a63ad114-7e13-5084-954f-fe012c677804"
+
+[[MuladdMacro]]
+deps = ["MacroTools", "Test"]
+git-tree-sha1 = "41e6e7c4b448afeaddaac7f496b414854f83b848"
+uuid = "46d2c3a1-f734-5fdb-9937-b9b9aeba4221"
+version = "0.2.1"
+
+[[MultiScaleArrays]]
+deps = ["DiffEqBase", "LinearAlgebra", "RecursiveArrayTools", "Statistics", "StochasticDiffEq", "Test", "TreeViews"]
+git-tree-sha1 = "4220ceea71186db2bb45cb817984c99e563f3662"
+uuid = "f9640e96-87f6-5992-9c3b-0743c6a49ffa"
+version = "1.4.0"
+
+[[NLSolversBase]]
+deps = ["Calculus", "DiffEqDiffTools", "DiffResults", "Distributed", "ForwardDiff", "LinearAlgebra", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "0c6f0e7f2178f78239cfb75310359eed10f2cacb"
+uuid = "d41bc354-129a-5804-8e4c-c37616107c6c"
+version = "7.3.1"
+
+[[NLsolve]]
+deps = ["DiffEqDiffTools", "Distances", "ForwardDiff", "LineSearches", "LinearAlgebra", "NLSolversBase", "Printf", "Random", "Reexport", "SparseArrays", "Test"]
+git-tree-sha1 = "413e54f04a4cbe9804089794eec6b06b2a43bc47"
+uuid = "2774e3e8-f4cf-5e23-947b-6d7e65073b56"
+version = "4.0.0"
+
+[[NNlib]]
+deps = ["Libdl", "LinearAlgebra", "Requires", "Statistics", "TimerOutputs"]
+git-tree-sha1 = "0c667371391fc6bb31f7f12f96a56a17098b3de8"
+uuid = "872c559c-99b0-510c-b3b7-b6c96a88d5cd"
+version = "0.6.0"
+
+[[NaNMath]]
+deps = ["Compat"]
+git-tree-sha1 = "ce3b85e484a5d4c71dd5316215069311135fa9f2"
+uuid = "77ba4419-2d1f-58cd-9bb1-8ffee604a2e3"
+version = "0.3.2"
+
+[[Observables]]
+deps = ["Test"]
+git-tree-sha1 = "dc02cec22747d1d10d9f70d8a1c03432b5bfbcd0"
+uuid = "510215fc-4207-5dde-b226-833fc4488ee2"
+version = "0.2.3"
+
+[[OffsetArrays]]
+git-tree-sha1 = "1af2f79c7eaac3e019a0de41ef63335ff26a0a57"
+uuid = "6fe1bfb0-de20-5000-8ca7-80f57d26f881"
+version = "0.11.1"
+
+[[Optim]]
+deps = ["Calculus", "DiffEqDiffTools", "ForwardDiff", "LineSearches", "LinearAlgebra", "NLSolversBase", "NaNMath", "Parameters", "PositiveFactorizations", "Printf", "Random", "SparseArrays", "StatsBase", "Test"]
+git-tree-sha1 = "a626e09c1f7f019b8f3a30a8172c7b82d2f4810b"
+uuid = "429524aa-4258-5aef-a3af-852621145aeb"
+version = "0.18.1"
+
+[[OrderedCollections]]
+deps = ["Random", "Serialization", "Test"]
+git-tree-sha1 = "c4c13474d23c60d20a67b217f1d7f22a40edf8f1"
+uuid = "bac558e1-5e72-5ebc-8fee-abe8a469f55d"
+version = "1.1.0"
+
+[[OrdinaryDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "DiffEqOperators", "ExponentialUtilities", "ForwardDiff", "GenericSVD", "LinearAlgebra", "Logging", "MuladdMacro", "NLsolve", "Parameters", "RecursiveArrayTools", "Reexport", "StaticArrays"]
+git-tree-sha1 = "7481f05badc75b80a62d0da988f09d6028c4fbb1"
+uuid = "1dea7af3-3e70-54e6-95c3-0bf5283fa5ed"
+version = "5.8.1"
+
+[[PDMats]]
+deps = ["Arpack", "LinearAlgebra", "SparseArrays", "SuiteSparse", "Test"]
+git-tree-sha1 = "8b68513175b2dc4023a564cb0e917ce90e74fd69"
+uuid = "90014a1f-27ba-587c-ab20-58faa44d9150"
+version = "0.9.7"
+
+[[Parameters]]
+deps = ["Markdown", "OrderedCollections", "REPL", "Test"]
+git-tree-sha1 = "70bdbfb2bceabb15345c0b54be4544813b3444e4"
+uuid = "d96e819e-fc66-5662-9728-84c9c7592b0a"
+version = "0.10.3"
+
+[[Parsers]]
+deps = ["Dates", "Test"]
+git-tree-sha1 = "db2b35dedab3c0e46dc15996d170af07a5ab91c9"
+uuid = "69de0a69-1ddd-5017-9359-2bf0b02dc9f0"
+version = "0.3.6"
+
+[[Pidfile]]
+deps = ["FileWatching", "Test"]
+git-tree-sha1 = "1ffd82728498b5071cde851bbb7abd780d4445f3"
+uuid = "fa939f87-e72e-5be4-a000-7fc836dbe307"
+version = "1.1.0"
+
+[[Pkg]]
+deps = ["Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "UUIDs"]
+uuid = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
+
+[[PlotThemes]]
+deps = ["PlotUtils", "Requires", "Test"]
+git-tree-sha1 = "f3afd2d58e1f6ac9be2cea46e4a9083ccc1d990b"
+uuid = "ccf2f8ad-2431-5c83-bf29-c5338b663b6a"
+version = "0.3.0"
+
+[[PlotUtils]]
+deps = ["Colors", "Dates", "Printf", "Random", "Reexport", "Test"]
+git-tree-sha1 = "8e87bbb778c26f575fbe47fd7a49c7b5ca37c0c6"
+uuid = "995b91a9-d308-5afd-9ec6-746e21dbc043"
+version = "0.5.8"
+
+[[Plots]]
+deps = ["Base64", "Contour", "Dates", "FixedPointNumbers", "GR", "GeometryTypes", "JSON", "LinearAlgebra", "Measures", "NaNMath", "Pkg", "PlotThemes", "PlotUtils", "Printf", "REPL", "Random", "RecipesBase", "Reexport", "Requires", "Showoff", "SparseArrays", "Statistics", "StatsBase", "UUIDs"]
+git-tree-sha1 = "c446e51959578de01b5a4efa72ca6f2460e38196"
+uuid = "91a5bcdd-55d7-5caf-9e0b-520d859cae80"
+version = "0.25.1"
+
+[[PoissonRandom]]
+deps = ["Random", "Statistics", "Test"]
+git-tree-sha1 = "44d018211a56626288b5d3f8c6497d28c26dc850"
+uuid = "e409e4f3-bfea-5376-8464-e040bb5c01ab"
+version = "0.4.0"
+
+[[PooledArrays]]
+git-tree-sha1 = "6e8c38927cb6e9ae144f7277c753714861b27d14"
+uuid = "2dfb63ee-cc39-5dd5-95bd-886bf059d720"
+version = "0.5.2"
+
+[[PositiveFactorizations]]
+deps = ["LinearAlgebra", "Test"]
+git-tree-sha1 = "957c3dd7c33895469760ce873082fbb6b3620641"
+uuid = "85a6dd25-e78a-55b7-8502-1745935b8125"
+version = "0.2.2"
+
+[[Printf]]
+deps = ["Unicode"]
+uuid = "de0858da-6303-5e67-8744-51eddeeeb8d7"
+
+[[Profile]]
+deps = ["Printf"]
+uuid = "9abbd945-dff8-562f-b5e8-e1ebf5ef1b79"
+
+[[QuadGK]]
+deps = ["DataStructures", "LinearAlgebra"]
+git-tree-sha1 = "438630b843c210b375b2a246329200c113acc61b"
+uuid = "1fd47b50-473d-5c70-9696-f719f8f3bcdc"
+version = "2.1.0"
+
+[[REPL]]
+deps = ["InteractiveUtils", "Markdown", "Sockets"]
+uuid = "3fa0cd96-eef1-5676-8a61-b3b8758bbffb"
+
+[[Random]]
+deps = ["Serialization"]
+uuid = "9a3f8284-a2c9-5f02-9a11-845980a1fd5c"
+
+[[RandomNumbers]]
+deps = ["Random", "Requires"]
+git-tree-sha1 = "1417be19c15706c1584d01e32662eb640a4cc908"
+uuid = "e6cf234a-135c-5ec9-84dd-332b85af5143"
+version = "1.3.0"
+
+[[RecipesBase]]
+git-tree-sha1 = "7bdce29bc9b2f5660a6e5e64d64d91ec941f6aa2"
+uuid = "3cdcf5f2-1ef4-517c-9805-6587b60abb01"
+version = "0.7.0"
+
+[[RecursiveArrayTools]]
+deps = ["ArrayInterface", "RecipesBase", "Requires", "StaticArrays", "Statistics", "Test"]
+git-tree-sha1 = "187ea7dd541955102c7035a6668613bdf52022ca"
+uuid = "731186ca-8d62-57ce-b412-fbd966d074cd"
+version = "0.20.0"
+
+[[RecursiveFactorization]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "54410ebd72cbb84d7b7678eb3da643f8e71181fc"
+uuid = "f2c3362d-daeb-58d1-803e-2bc74f2840b4"
+version = "0.0.1"
+
+[[Reexport]]
+deps = ["Pkg"]
+git-tree-sha1 = "7b1d07f411bc8ddb7977ec7f377b97b158514fe0"
+uuid = "189a3867-3050-52da-a836-e630ba90ab69"
+version = "0.2.0"
+
+[[Requires]]
+deps = ["Test"]
+git-tree-sha1 = "f6fbf4ba64d295e146e49e021207993b6b48c7d1"
+uuid = "ae029012-a4dd-5104-9daa-d747884805df"
+version = "0.5.2"
+
+[[ResettableStacks]]
+deps = ["Random", "StaticArrays", "Test"]
+git-tree-sha1 = "8b4f6cf3c97530e1ba7177ad3bc2b134373da851"
+uuid = "ae5879a3-cd67-5da8-be7f-38c6eb64a37b"
+version = "0.6.0"
+
+[[Rmath]]
+deps = ["BinaryProvider", "Libdl", "Random", "Statistics", "Test"]
+git-tree-sha1 = "9a6c758cdf73036c3239b0afbea790def1dabff9"
+uuid = "79098fc4-a85e-5d69-aa6a-4863f24498fa"
+version = "0.5.0"
+
+[[Roots]]
+deps = ["Printf", "Statistics", "Test"]
+git-tree-sha1 = "7228278e31d6d0e22a1ae0b41ea9a0df2859f33d"
+uuid = "f2b01f46-fcfa-551c-844a-d8ac1e96c665"
+version = "0.8.1"
+
+[[SHA]]
+uuid = "ea8e919c-243c-51af-8825-aaa63cd721ce"
+
+[[Serialization]]
+uuid = "9e88b42a-f829-5b0c-bbe9-9e923198166b"
+
+[[SharedArrays]]
+deps = ["Distributed", "Mmap", "Random", "Serialization"]
+uuid = "1a1011a3-84de-559e-8e89-a11a2f7dc383"
+
+[[ShiftedArrays]]
+deps = ["OffsetArrays", "RecursiveArrayTools", "Test"]
+git-tree-sha1 = "b1aa84666a23a31cebcdcb848e62428968789287"
+uuid = "1277b4bf-5013-50f5-be3d-901d8477a67a"
+version = "0.5.0"
+
+[[Showoff]]
+deps = ["Dates"]
+git-tree-sha1 = "e032c9df551fb23c9f98ae1064de074111b7bc39"
+uuid = "992d4aef-0814-514b-bc4d-f2e9a6c4116f"
+version = "0.3.1"
+
+[[Sockets]]
+uuid = "6462fe0b-24de-5631-8697-dd941f90decc"
+
+[[SortingAlgorithms]]
+deps = ["DataStructures", "Random", "Test"]
+git-tree-sha1 = "03f5898c9959f8115e30bc7226ada7d0df554ddd"
+uuid = "a2af1166-a08f-5f64-846c-94a0d3cef48c"
+version = "0.3.1"
+
+[[SparseArrays]]
+deps = ["LinearAlgebra", "Random"]
+uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
+
+[[SpecialFunctions]]
+deps = ["BinDeps", "BinaryProvider", "Libdl", "Test"]
+git-tree-sha1 = "0b45dc2e45ed77f445617b99ff2adf0f5b0f23ea"
+uuid = "276daf66-3868-5448-9aa4-cd146d93841b"
+version = "0.7.2"
+
+[[StaticArrays]]
+deps = ["LinearAlgebra", "Random", "Statistics"]
+git-tree-sha1 = "db23bbf50064c582b6f2b9b043c8e7e98ea8c0c6"
+uuid = "90137ffa-7385-5640-81b9-e52037218182"
+version = "0.11.0"
+
+[[Statistics]]
+deps = ["LinearAlgebra", "SparseArrays"]
+uuid = "10745b16-79ce-11e8-11f9-7d13ad32a3b2"
+
+[[StatsBase]]
+deps = ["DataStructures", "LinearAlgebra", "Missings", "Printf", "Random", "SortingAlgorithms", "SparseArrays", "Statistics"]
+git-tree-sha1 = "8a0f4b09c7426478ab677245ab2b0b68552143c7"
+uuid = "2913bbd2-ae8a-5f71-8c99-4fb6c76f3a91"
+version = "0.30.0"
+
+[[StatsFuns]]
+deps = ["Rmath", "SpecialFunctions", "Test"]
+git-tree-sha1 = "b3a4e86aa13c732b8a8c0ba0c3d3264f55e6bb3e"
+uuid = "4c63d2b9-4356-54db-8cca-17b64c39e42c"
+version = "0.8.0"
+
+[[StatsModels]]
+deps = ["CategoricalArrays", "DataStructures", "LinearAlgebra", "Missings", "ShiftedArrays", "SparseArrays", "StatsBase", "Tables"]
+git-tree-sha1 = "f004c23db67aeecb4bba94d08c79580af851b21b"
+uuid = "3eaba693-59b7-5ba5-a881-562e759f1c8d"
+version = "0.6.1"
+
+[[SteadyStateDiffEq]]
+deps = ["Compat", "DiffEqBase", "DiffEqCallbacks", "LinearAlgebra", "NLsolve", "Reexport", "Test"]
+git-tree-sha1 = "fe9852d18c3e30f384003da50d6049e5fbc97071"
+uuid = "9672c7b4-1e72-59bd-8a11-6ac3964bc41f"
+version = "1.4.0"
+
+[[StochasticDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "DiffEqNoiseProcess", "DiffEqOperators", "FillArrays", "ForwardDiff", "LinearAlgebra", "Logging", "MuladdMacro", "NLsolve", "Parameters", "Random", "RandomNumbers", "RecursiveArrayTools", "Reexport", "StaticArrays"]
+git-tree-sha1 = "83be179dc849f11f83dcfa715c7818ef551a0f6c"
+uuid = "789caeaf-c7a9-5a7d-9973-96adeb23e2a0"
+version = "6.5.0"
+
+[[SuiteSparse]]
+deps = ["Libdl", "LinearAlgebra", "Serialization", "SparseArrays"]
+uuid = "4607b0f0-06f3-5cda-b6b1-a6196a1729e9"
+
+[[Sundials]]
+deps = ["BinaryProvider", "DataStructures", "DiffEqBase", "Libdl", "LinearAlgebra", "Logging", "Reexport", "SparseArrays", "SuiteSparse"]
+git-tree-sha1 = "9af4eb72683f0dafe84c6a5bd31aea1ebca4d46c"
+uuid = "c3572dad-4567-51f8-b174-8c6c989267f4"
+version = "3.6.1"
+
+[[TableTraits]]
+deps = ["IteratorInterfaceExtensions"]
+git-tree-sha1 = "b1ad568ba658d8cbb3b892ed5380a6f3e781a81e"
+uuid = "3783bdb8-4a98-5b6b-af9a-565f29a5fe9c"
+version = "1.0.0"
+
+[[Tables]]
+deps = ["DataValueInterfaces", "IteratorInterfaceExtensions", "LinearAlgebra", "Requires", "TableTraits", "Test"]
+git-tree-sha1 = "c93aafd5c45f850c653ec1c45857ba2151835f95"
+uuid = "bd369af6-aec1-5ad0-b16a-f7cc5008161c"
+version = "0.2.7"
+
+[[Test]]
+deps = ["Distributed", "InteractiveUtils", "Logging", "Random"]
+uuid = "8dfed614-e22c-5e08-85e1-65c5234f0b40"
+
+[[TimerOutputs]]
+deps = ["Crayons", "Printf", "Test", "Unicode"]
+git-tree-sha1 = "b80671c06f8f8bae08c55d67b5ce292c5ae2660c"
+uuid = "a759f4b9-e2f1-59dc-863e-4aeb61b1ea8f"
+version = "0.5.0"
+
+[[Tokenize]]
+git-tree-sha1 = "0de343efc07da00cd449d5b04e959ebaeeb3305d"
+uuid = "0796e94c-ce3b-5d07-9a54-7f471281c624"
+version = "0.5.4"
+
+[[Tracker]]
+deps = ["Adapt", "DiffRules", "ForwardDiff", "LinearAlgebra", "MacroTools", "NNlib", "NaNMath", "Printf", "Random", "Requires", "SpecialFunctions", "Statistics", "Test"]
+git-tree-sha1 = "327342fec6e09f68ced0c2dc5731ed475e4b696b"
+uuid = "9f7883ad-71c0-57eb-9f7f-b5c9e6d3789c"
+version = "0.2.2"
+
+[[TranscodingStreams]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "a25d8e5a28c3b1b06d3859f30757d43106791919"
+uuid = "3bb67fe8-82b1-5028-8e26-92a6c54297fa"
+version = "0.9.4"
+
+[[Trebuchet]]
+deps = ["DiffEqBase", "JSExpr", "OrdinaryDiffEq", "WebIO"]
+git-tree-sha1 = "c1daf264ca0c050381be6258b5e311615ea5f250"
+uuid = "98b73d46-197d-11e9-11eb-69a6ff759d3a"
+version = "0.1.0"
+
+[[TreeViews]]
+deps = ["Test"]
+git-tree-sha1 = "8d0d7a3fe2f30d6a7f833a5f19f7c7a5b396eae6"
+uuid = "a2a6695c-b41b-5b7d-aed9-dbfdeacea5d7"
+version = "0.3.0"
+
+[[URIParser]]
+deps = ["Test", "Unicode"]
+git-tree-sha1 = "6ddf8244220dfda2f17539fa8c9de20d6c575b69"
+uuid = "30578b45-9adc-5946-b283-645ec420af67"
+version = "0.4.0"
+
+[[UUIDs]]
+deps = ["Random", "SHA"]
+uuid = "cf7118a7-6976-5b1a-9a39-7adc72f591a4"
+
+[[Unicode]]
+uuid = "4ec0a83e-493e-50e2-b9ac-8f72acf5a8f5"
+
+[[WeakRefStrings]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "9a0bb82eede528debe631b642eeb48a631a69bc2"
+uuid = "ea10d353-3f73-51f8-a26c-33c1cb351aa5"
+version = "0.6.1"
+
+[[WebIO]]
+deps = ["AssetRegistry", "Base64", "Compat", "Distributed", "FunctionalCollections", "JSON", "Logging", "Observables", "Random", "Requires", "Sockets", "UUIDs", "WebSockets", "Widgets"]
+git-tree-sha1 = "458ebbd85da851b01bed01e6321b0d8f4c7044b0"
+uuid = "0f1e0344-ec1d-5b48-a673-e5cf874b6c29"
+version = "0.8.6"
+
+[[WebSockets]]
+deps = ["Base64", "Dates", "Distributed", "HTTP", "Logging", "Random", "Sockets", "Test"]
+git-tree-sha1 = "13f763d38c7a05688938808b49cb29b18b60c8c8"
+uuid = "104b5d7c-a370-577a-8038-80a2059c5097"
+version = "1.5.2"
+
+[[Widgets]]
+deps = ["Colors", "Dates", "Observables", "OrderedCollections", "Test"]
+git-tree-sha1 = "c53befc70c6b91eaa2a9888c2f6ac2d92720a81b"
+uuid = "cc8bc4a8-27d6-5769-a93b-9d913e69aa62"
+version = "0.6.1"
+
+[[ZipFile]]
+deps = ["BinaryProvider", "Libdl", "Printf"]
+git-tree-sha1 = "580ce62b6c14244916cc28ad54f8a2e2886f843d"
+uuid = "a5390f91-8eb1-5f08-bee0-b1d1ffed6cea"
+version = "0.8.3"
+
+[[Zygote]]
+deps = ["DiffRules", "FillArrays", "ForwardDiff", "IRTools", "InteractiveUtils", "LinearAlgebra", "MacroTools", "NNlib", "NaNMath", "Random", "Requires", "SpecialFunctions", "Statistics"]
+git-tree-sha1 = "520d65c5e5554473863d738bde053f5f6769d3be"
+uuid = "e88e6eb3-aa80-5325-afca-941959d7151f"
+version = "0.3.2"
diff --git a/Courses/Differentiable Programming/Project.toml b/Courses/Differentiable Programming/Project.toml
new file mode 100644
index 0000000..3c94cc3
--- /dev/null
+++ b/Courses/Differentiable Programming/Project.toml
@@ -0,0 +1,12 @@
+[deps]
+BenchmarkTools = "6e4b80f9-dd63-53aa-95a3-0cdb28fa8baf"
+CSV = "336ed68f-0bac-5ca0-87d4-7b16caf5d00b"
+DiffEqFlux = "aae7a2af-3d4f-5e19-a356-7da93b79d9d0"
+DifferentialEquations = "0c46a032-eb83-5123-abaf-570d42b7fbaa"
+Flux = "587475ba-b771-5e3f-ad9e-33799f191a9c"
+ForwardDiff = "f6369f11-7733-5829-9624-2563aa707210"
+Literate = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
+Optim = "429524aa-4258-5aef-a3af-852621145aeb"
+Plots = "91a5bcdd-55d7-5caf-9e0b-520d859cae80"
+Trebuchet = "98b73d46-197d-11e9-11eb-69a6ff759d3a"
+Zygote = "e88e6eb3-aa80-5325-afca-941959d7151f"
diff --git a/Manifest.toml b/Manifest.toml
index fb2c933..d0f2265 100644
--- a/Manifest.toml
+++ b/Manifest.toml
@@ -4,8 +4,10 @@
uuid = "2a0f44e3-6c83-55bd-87e4-b1978d98bd5f"
[[BinaryProvider]]
-deps = ["Compat", "CredentialsHandler", "Libdl", "Pkg", "SHA", "TOML", "Test"]
+deps = ["Libdl", "Logging", "SHA"]
+git-tree-sha1 = "8153fd64131cd00a79544bb23788877741f627bb"
uuid = "b99e7846-7c00-51b0-8f62-c81ae34c0232"
+version = "0.5.5"
[[Compat]]
deps = ["Base64", "Dates", "DelimitedFiles", "Distributed", "InteractiveUtils", "LibGit2", "Libdl", "LinearAlgebra", "Markdown", "Mmap", "Pkg", "Printf", "REPL", "Random", "Serialization", "SharedArrays", "Sockets", "SparseArrays", "Statistics", "Test", "UUIDs", "Unicode"]
@@ -13,9 +15,11 @@ git-tree-sha1 = "84aa74986c5b9b898b0d1acaf3258741ee64754f"
uuid = "34da2185-b29b-5c13-b0c7-acf172513d20"
version = "2.1.0"
-[[CredentialsHandler]]
-deps = ["Base64", "HTTP", "TOML"]
-uuid = "864e158e-919d-11e8-198e-cfe890ec4681"
+[[Conda]]
+deps = ["JSON", "VersionParsing"]
+git-tree-sha1 = "9a11d428dcdc425072af4aea19ab1e8c3e01c032"
+uuid = "8f4d0f93-b110-5947-807f-2305c1781a2d"
+version = "1.3.0"
[[Dates]]
deps = ["Printf"]
@@ -26,18 +30,26 @@ deps = ["Mmap"]
uuid = "8bb1440f-4735-579b-a4ab-409b98df4dab"
[[Distributed]]
-deps = ["LinearAlgebra", "Random", "Serialization", "Sockets"]
+deps = ["Random", "Serialization", "Sockets"]
uuid = "8ba89e20-285c-5b6f-9357-94700520ee1b"
-[[HTTP]]
-deps = ["Base64", "Dates", "Distributed", "IniFile", "MbedTLS", "Sockets", "Test"]
-uuid = "cd3eb016-35fb-5094-929b-558a96fad6f3"
+[[FileWatching]]
+uuid = "7b1f6079-737a-58dc-b8bc-7a2ca5c1b5ee"
-[[IniFile]]
-uuid = "83e8ac13-25f8-5344-8a64-a9f2b223428f"
+[[Glob]]
+deps = ["Compat", "Test"]
+git-tree-sha1 = "c72f1fcb7d17426de1e8af2e948dfb3de1116eed"
+uuid = "c27321d9-0574-5035-807b-f59d2c89b15c"
+version = "1.2.0"
+
+[[IJulia]]
+deps = ["Base64", "Conda", "Dates", "InteractiveUtils", "JSON", "Markdown", "MbedTLS", "Pkg", "Printf", "REPL", "Random", "SoftGlobalScope", "Test", "UUIDs", "ZMQ"]
+git-tree-sha1 = "8eb8459d806de665f1347b25e9ad9428c2609f0f"
+uuid = "7073ff75-c697-5162-941a-fcdaad2a7d2a"
+version = "1.18.1"
[[InteractiveUtils]]
-deps = ["LinearAlgebra", "Markdown"]
+deps = ["Markdown"]
uuid = "b77e0a4c-d291-57a0-90e8-8db25a27a240"
[[JSON]]
@@ -46,14 +58,6 @@ git-tree-sha1 = "1f7a25b53ec67f5e9422f1f551ee216503f4a0fa"
uuid = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
version = "0.20.0"
-[[JuliaAcademyData]]
-deps = ["Pkg"]
-git-tree-sha1 = "6cc6db29d6560619be88d0075d697047eb484f92"
-repo-rev = "master"
-repo-url = "https://github.com/JuliaComputing/JuliaAcademyData.jl"
-uuid = "18b7da76-0988-5e3b-acac-6290be3a708f"
-version = "0.1.0"
-
[[LibGit2]]
uuid = "76f85450-5226-5b5a-8eaa-529ad045b433"
@@ -78,14 +82,16 @@ deps = ["Base64"]
uuid = "d6f4376e-aef5-505a-96c1-9c027394607a"
[[MbedTLS]]
-deps = ["BinaryProvider", "Dates", "Libdl", "Pkg", "Random", "Sockets"]
+deps = ["BinaryProvider", "Dates", "Distributed", "Libdl", "Random", "Sockets", "Test"]
+git-tree-sha1 = "2d94286a9c2f52c63a16146bb86fd6cdfbf677c6"
uuid = "739be429-bea8-5141-9913-cc70e7f3736d"
+version = "0.6.8"
[[Mmap]]
uuid = "a63ad114-7e13-5084-954f-fe012c677804"
[[Pkg]]
-deps = ["BinaryProvider", "CredentialsHandler", "Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "TOML", "UUIDs"]
+deps = ["Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "UUIDs"]
uuid = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
[[Printf]]
@@ -113,6 +119,12 @@ uuid = "1a1011a3-84de-559e-8e89-a11a2f7dc383"
[[Sockets]]
uuid = "6462fe0b-24de-5631-8697-dd941f90decc"
+[[SoftGlobalScope]]
+deps = ["Test"]
+git-tree-sha1 = "012661b70364840fcd380912d878d96f7bf95ff3"
+uuid = "b85f4697-e234-5449-a836-ec8e2f98b302"
+version = "1.0.10"
+
[[SparseArrays]]
deps = ["LinearAlgebra", "Random"]
uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
@@ -121,17 +133,25 @@ uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
deps = ["LinearAlgebra", "SparseArrays"]
uuid = "10745b16-79ce-11e8-11f9-7d13ad32a3b2"
-[[TOML]]
-deps = ["Dates"]
-uuid = "9d418dce-91a8-11e8-0173-7b01a971d501"
-
[[Test]]
deps = ["Distributed", "InteractiveUtils", "Logging", "Random"]
uuid = "8dfed614-e22c-5e08-85e1-65c5234f0b40"
[[UUIDs]]
-deps = ["Random"]
+deps = ["Random", "SHA"]
uuid = "cf7118a7-6976-5b1a-9a39-7adc72f591a4"
[[Unicode]]
uuid = "4ec0a83e-493e-50e2-b9ac-8f72acf5a8f5"
+
+[[VersionParsing]]
+deps = ["Compat"]
+git-tree-sha1 = "c9d5aa108588b978bd859554660c8a5c4f2f7669"
+uuid = "81def892-9a0e-5fdd-b105-ffc91e053289"
+version = "1.1.3"
+
+[[ZMQ]]
+deps = ["BinaryProvider", "FileWatching", "Libdl", "Sockets", "Test"]
+git-tree-sha1 = "34e7ac2d1d59d19d0e86bde99f1f02262bfa1613"
+uuid = "c2297ded-f4af-51ae-bb23-16f91089e4e1"
+version = "1.0.0"
diff --git a/Project.toml b/Project.toml
index ebae8eb..116ec28 100644
--- a/Project.toml
+++ b/Project.toml
@@ -3,7 +3,9 @@ uuid = "a2de2ff4-d7bb-11e8-2879-f9ef9fa2c94f"
version = "0.1.0"
[deps]
-JuliaAcademyData = "18b7da76-0988-5e3b-acac-6290be3a708f"
+Glob = "c27321d9-0574-5035-807b-f59d2c89b15c"
+IJulia = "7073ff75-c697-5162-941a-fcdaad2a7d2a"
+JSON = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
Literate = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
Pkg = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
+#
+# But let's examine that line-fitting first as its simplicity makes a number of
+# points clear. To begin, let's load some data.
+
+using DifferentialEquations, CSV #src
+import Random #src
+Random.seed!(20) #src
+generate_data(ts) = solve(ODEProblem([1.0,1.0],(0.0,10.0),[1.5,1.0,3.0,1.0]) do du,u,p,t; du[1] = p[1]*u[1] - p[2]*prod(u); du[2] = -p[3]*u[2] + p[4]*prod(u); end, saveat=ts)[1,:].*(1.0.+0.02.*randn.()).+0.05.*randn.() #src
+ts = 0:.005:1 #src
+ys = generate_data(ts) #src
+CSV.write(datapath("data/020-descent-data.csv"), (t=ts, y=ys)) #src
+
+using CSV
+df = CSV.read(datapath("data/020-descent-data.csv"))
+#-
+using Plots
+scatter(df.t, df.y, xlabel="time", label="data")
+
+# Now we want to fit some model to this data — for a linear model we just need
+# two parameters:
+#
+# $$
+# y = m x + b
+# $$
+#
+# Lets create a structure that represents this:
+
+mutable struct LinearModel
+ m::Float64
+ b::Float64
+end
+(model::LinearModel)(x) = model.m*x + model.b
+
+# And create a randomly picked model to see how we do:
+linear = LinearModel(randn(), randn())
+plot!(df.t, linear.(df.t), label="model")
+
+# Of course, we just chose our `m` and `b` at random here, of course it's not
+# going to fit our data well! Let's quantify how far we are from an ideal line
+# with a _loss_ function:
+
+loss(f, xs, ys) = sum((f.(xs) .- ys).^2)
+loss(linear, df.t, df.y)
+
+# That's a pretty big number — and we want to decrease it. Let's update our plot
+# to include this loss value in the legend so we can keep track:
+
+p = scatter(df.t, df.y, xlabel="time", label="data")
+plot!(p, df.t, linear.(df.t), label="model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# And now we want to try to improve the fit. To do so, we just need to make
+# the loss function as small as possible. We can of course simply try a bunch
+# of values and brute-force a "good" solution. Plotting this as a three-dimensional
+# surface gives us the imagery of a hill, and our goal is to find our way to the bottom:
+
+ms, bs = (-1:.01:6, -2:.05:2.5)
+surface(ms, bs, [loss(LinearModel(m, b), df.t, df.y) for b in bs for m in ms], xlabel="m values", ylabel="b values", title="loss value")
+
+# A countour plot makes it a bit more obvious where the minimum is:
+
+contour(ms, bs, [loss(LinearModel(m, b), df.t, df.y) for b in bs for m in ms], levels=150, xlabel="m values", ylabel="b values")
+
+# But building those graphs are expensive! And it becomes completely intractible as soon as we
+# have more than a few parameters to fit. We can instead just try nudging the
+# current model's values to simply figure out which direction is "downhill":
+
+linear.m += 0.1
+plot!(p, df.t, linear.(df.t), label="new model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# We'll either have made things better or worse — but either way it's easy to
+# see which way to change `m` in order to improve our model.
+#
+# Essentially, what we're doing here is we're finding the derivative of our
+# loss function with respect to `m`, but again, there's a bit to be desired
+# here. Instead of evaluating the loss function twice and observing the difference,
+# we can just ask Julia for the derivative! This is the heart of differentiable
+# programming — the ability to ask a _complete program_ for its derivative.
+#
+# There are several techniques that you can use to compute the derivative. We'll
+# use the [Zygote package](https://fluxml.ai/Zygote.jl/latest/) first. It will
+# take a second as it compiles the "adjoint" code to compute the derivatives.
+# Since we're doing this in multiple dimensions, the two derivatives together
+# are called the gradient:
+
+using Zygote
+grads = Zygote.gradient(linear) do m
+ return loss(m, df.t, df.y)
+end
+grads
+
+# So there we go! Zygote saw that the model was gave it — `linear` — had two fields and thus
+# it computed the derivative of the loss function with respect to those two
+# parameters.
+#
+# Now we know the slope of our loss function — and thus
+# we know which way to move each parameter to improve it! We just need to iteratively walk
+# downhill! We don't want to take too large a step, so we'll multiply each
+# derivative by a "learning rate," typically called `η`.
+η = 0.001
+linear.m -= η*grads[1][].m
+linear.b -= η*grads[1][].b
+
+plot!(p, df.t, linear.(df.t), label="updated model: loss $(round(Int, loss(linear, df.t, df.y)))")
+
+# Now we just need to do this a bunch of times!
+
+for i in 1:200
+ grads = Zygote.gradient(linear) do m
+ return loss(m, df.t, df.y)
+ end
+ linear.m -= η*grads[1][].m
+ linear.b -= η*grads[1][].b
+ i > 40 && i % 10 != 1 && continue
+#nb IJulia.clear_output(true)
+ scatter(df.t, df.y, label="data", xlabel="time", legend=:topleft)
+ display(plot!(df.t, linear.(df.t), label="model (loss: $(round(loss(linear, df.t, df.y), digits=3)))"))
+end
+
+#src === CREATING GIF ===
+f = let #src
+ linear = LinearModel(randn(), randn()) #src
+ f = @gif for i in 1:150 #src
+ grads = Zygote.gradient(linear) do m #src
+ return loss(m, df.t, df.y) #src
+ end #src
+ linear.m -= η*grads[1][].m #src
+ linear.b -= η*grads[1][].b #src
+ scatter(df.t, df.y, label="data", xlabel="time", legend=:topleft) #src
+ plot!(df.t, linear.(df.t), label="model (loss: $(round(loss(linear, df.t, df.y), digits=3)))") #src
+ end #src
+ mv(f.filename, datapath("images/020-linear.gif")) #src
+end #src
+
+
+
+# That's looking pretty good now! You might be saying this is crazy — I know
+# how to do a least squares fit! And you'd be right — in this case you can
+# easily do this with a linear solve of the system of equations:
+m, b = [df.t ones(size(df.t))] \ df.y
+
+@show (m, b)
+@show (linear.m, linear.b);
+
+# ## Exercise: Use gradient descent to fit a quadratic model to the data
+#
+# Obviously a linear fit leaves a bit to be desired here. Try to use the same
+# framework to fit a quadratic model. Check your answer against the algebraic
+# solution with the `\` operator.
+
+struct PolyModel
+ p::Vector{Float64}
+end
+function (m::PolyModel)(x)
+ r = m.p[1]*x^0
+ for i in 2:length(m.p)
+ r += m.p[i]*x^(i-1)
+ end
+ return r
+end
+poly = PolyModel(rand(3))
+loss(poly, df.t, df.y)
+η = 0.001
+for i in 1:1000
+ grads = Zygote.gradient(poly) do m
+ return loss(m, df.t, df.y)
+ end
+ poly.p .-= η.*grads[1].p
+end
+scatter(df.t, df.y, label="data", legend=:topleft)
+plot!(df.t, poly.(df.t), label="model by descent")
+plot!(df.t, PolyModel([df.t.^0 df.t df.t.^2] \ df.y).(df.t), label="model by linear solve")
+
+# ## Nonlinearities
+#
+# Let's see what happens when load a bit more data:
+
+let #src
+ ts = 0:.04:8 #src
+ ys = generate_data(ts) #src
+ CSV.write(datapath("data/020-descent-data-2.csv"), (t=ts, y=ys)) #src
+end #src
+df2 = CSV.read(datapath("data/020-descent-data-2.csv"))
+scatter(df2.t, df2.y, xlabel="t", label="more data")
+
+# Now what? This clearly won't be fit well with a low-order polynomial, and
+# even a high-order polynomial will get things wrong once we try to see what
+# will happen in the "future"!
+#
+# Let's use a bit of knowledge about where this data comes from: these happen
+# to be the number of rabbits in a predator-prey system! We can express the
+# general behavior with a pair of differential equations:
+#
+# $$
+# x' = \alpha x - \beta x y \\
+# y' = -\delta y + \gamma x y
+# $$
+#
+# * $x$ is the number of rabbits (🐰)
+# * $y$ is the number of wolves (🐺)
+# * $\alpha$ and $\beta$ describe the growth and death rates for the rabbits
+# * $\gamma$ and $\delta$ describe the growth and death rates for the wolves
+#
+# But we don't know what those rate constants are — all we have is the population
+# of rabbits over time.
+#
+# These are the classic Lotka-Volterra equations, and can be expressed in Julia
+# using the [DifferentialEquations](https://github.com/JuliaDiffEq/DifferentialEquations.jl) package:
+using DifferentialEquations
+function rabbit_wolf(du,u,p,t)
+ 🐰, 🐺 = u
+ α, β, δ, γ = p
+ du[1] = α*🐰 - β*🐰*🐺
+ du[2] = -δ*🐺 + γ*🐰*🐺
+end
+u0 = [1.0,1.0]
+tspan = extrema(df2.t)
+p = rand(4).+1 # We don't know what this is!
+## But lets see what the model looks like right now:
+prob = ODEProblem(rabbit_wolf,u0,tspan,p)
+sol = solve(prob, Tsit5(), saveat=df2.t)
+
+scatter(df2.t, df2.y, xlabel="t", label="more data")
+plot!(sol, label=["rabbits","wolves"])
+
+# So we're going to have to improve this — unlike the previous examples, we don't
+# have an easy algebraic solution here! But let's try using gradient descent.
+# The easiest way to get gradients out of a differential equation solver right
+# now is through the [DiffEqFlux package](https://github.com/JuliaDiffEq/DiffEqFlux.jl), and instead of manually converging,
+# we can use the Flux package to automatically (and more smartly) handle the gradient descent. Just
+# like before, though, we compute the loss of the model evaluation — and in this
+# case the model is _solving a differential equation!_
+using Flux, DiffEqFlux
+p = Flux.param(ones(4))
+diffeq_loss(p, xs, ys) = sum(abs2, diffeq_rd(p,prob,Tsit5(),saveat=df2.t)[1,:] .- df2.y)
+
+# This works slightly differently — we now track the gradients directly in the
+# p vector:
+p.grad
+#-
+l = diffeq_loss(p, df2.t, df2.y)
+#-
+DiffEqFlux.Tracker.back!(l) # we need to back-propagate our tracking of the gradients
+p.grad # but now we can see the gradients involved in that computation!
+
+# So now we can do exactly the same thing as before: iteratively update the parameters
+# to descend to a (hopefully) well-fit model:
+#
+# ```julia
+# p.data .-= η*p.grad
+# ```
+#
+# But we can be a bit smarter about this just by asking Flux to handle everything
+# with its train! function and associated functionality:
+
+data = Iterators.repeated((df2.t, df2.y), 150)
+opt = ADAM(0.1)
+history = Any[] #src
+cb = function () #callback function to observe training
+#nb IJulia.clear_output(true)
+ plt = scatter(df2.t, df2.y, label="data", ylabel="population (thousands)", xlabel="t")
+ display(plot!(plt, solve(remake(prob,p=Flux.data(p)),Tsit5(),saveat=0.1),
+ ylim=(0,8), label=["rabbits","wolves"], title="loss: $(round(Flux.data(diffeq_loss(p, df2.t, df2.y)), digits=3))"))
+ push!(history, plt) #src
+end
+Flux.train!((xs, ys)->diffeq_loss(p, xs, ys), [p], data, opt, cb = cb)
+
+f = @gif for i in 1:length(history) #src
+ plot(history[i]) #src
+end #src
+mv(f.filename, datapath("images/020-diffeq.gif")) #src
+
+# # Summary
+#
+# You can now see the power of differentiating whole programs — we can easily
+# and efficiently tune parameters without brute forcing solutions. Gradient
+# descent easily extends to machine learning and artificial intelligence
+# applications — and there are a number of tricks that can increase its efficiency
+# and help avoid local minima. There are a variety of other places where knowing the gradient can
+# be powerful and helpful.
diff --git a/Courses/Differentiable Programming/030 Neural Differential Equations.jl b/Courses/Differentiable Programming/030 Neural Differential Equations.jl
new file mode 100644
index 0000000..0b0f013
--- /dev/null
+++ b/Courses/Differentiable Programming/030 Neural Differential Equations.jl
@@ -0,0 +1,86 @@
+using Flux, DiffEqFlux, StochasticDiffEq, Plots, DiffEqMonteCarlo
+
+u0 = Float32[2.; 0.]
+datasize = 30
+tspan = (0.0f0,1.0f0)
+
+function trueODEfunc(du,u,p,t)
+ true_A = [-0.1 2.0; -2.0 -0.1]
+ du .= ((u.^3)'true_A)'
+end
+t = range(tspan[1],tspan[2],length=datasize)
+mp = Float32[0.2,0.2]
+function true_noise_func(du,u,p,t)
+ du .= mp.*u
+end
+prob = SDEProblem(trueODEfunc,true_noise_func,u0,tspan)
+
+# Take a typical sample from the mean
+monte_prob = MonteCarloProblem(prob)
+monte_sol = solve(monte_prob,SOSRI(),num_monte = 100)
+monte_sum = MonteCarloSummary(monte_sol)
+sde_data = Array(timeseries_point_mean(monte_sol,t))
+
+dudt = Chain(x -> x.^3,
+ Dense(2,50,tanh),
+ Dense(50,2))
+ps = Flux.params(dudt)
+n_sde = x->neural_dmsde(dudt,x,mp,tspan,SOSRI(),saveat=t,reltol=1e-1,abstol=1e-1)
+
+pred = n_sde(u0) # Get the prediction using the correct initial condition
+
+dudt_(u,p,t) = Flux.data(dudt(u))
+g(u,p,t) = mp.*u
+nprob = SDEProblem(dudt_,g,u0,(0.0f0,1.2f0),nothing)
+
+monte_nprob = MonteCarloProblem(nprob)
+monte_nsol = solve(monte_nprob,SOSRI(),num_monte = 100)
+monte_nsum = MonteCarloSummary(monte_nsol)
+#plot(monte_nsol,color=1,alpha=0.3)
+p1 = plot(monte_nsum, title = "Neural SDE: Before Training")
+scatter!(p1,t,sde_data',lw=3)
+
+scatter(t,sde_data[1,:],label="data")
+scatter!(t,Flux.data(pred[1,:]),label="prediction")
+
+function predict_n_sde()
+ n_sde(u0)
+end
+loss_n_sde1() = sum(abs2,sde_data .- predict_n_sde())
+loss_n_sde10() = sum([sum(abs2,sde_data .- predict_n_sde()) for i in 1:10])
+Flux.back!(loss_n_sde1())
+
+data = Iterators.repeated((), 10)
+opt = ADAM(0.025)
+cb = function () #callback function to observe training
+ sample = predict_n_sde()
+ # loss against current data
+ display(sum(abs2,sde_data .- sample))
+ # plot current prediction against data
+ cur_pred = Flux.data(sample)
+ pl = scatter(t,sde_data[1,:],label="data")
+ scatter!(pl,t,cur_pred[1,:],label="prediction")
+ display(plot(pl))
+end
+
+# Display the SDE with the initial parameter values.
+cb()
+
+Flux.train!(loss_n_sde1 , ps, Iterators.repeated((), 100), opt, cb = cb)
+Flux.train!(loss_n_sde10, ps, Iterators.repeated((), 20), opt, cb = cb)
+
+dudt_(u,p,t) = Flux.data(dudt(u))
+g(u,p,t) = mp.*u
+nprob = SDEProblem(dudt_,g,u0,(0.0f0,1.2f0),nothing)
+
+monte_nprob = MonteCarloProblem(nprob)
+monte_nsol = solve(monte_nprob,SOSRI(),num_monte = 100)
+monte_nsum = MonteCarloSummary(monte_nsol)
+#plot(monte_nsol,color=1,alpha=0.3)
+p2 = plot(monte_nsum, title = "Neural SDE: After Training", xlabel="Time")
+scatter!(p2,t,sde_data',lw=3,label=["x" "y" "z" "y"])
+
+plot(p1,p2,layout=(2,1))
+
+savefig("neural_sde.pdf")
+savefig("neural_sde.png")
diff --git a/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl b/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl
new file mode 100644
index 0000000..6cc7a7f
--- /dev/null
+++ b/Courses/Differentiable Programming/040 Reinforcing Trebuchet.jl
@@ -0,0 +1,260 @@
+# # How To Aim Your Flagon
+
+#-
+
+# ## Loading your Trebuchet
+
+#-
+
+# Today we practice the ancient medieval art of throwing stuff. First up, we load our trebuchet simulator, Trebuchet.jl.
+
+using Trebuchet
+
+# We can see what the trebuchet looks like, by explicitly creating a trebuchet state, running a simulation, and visualising the trajectory.
+
+t = TrebuchetState()
+simulate(t)
+visualise(t)
+
+# For training and optimisation, we don't need the whole visualisation, just a simple function that accepts and produces numbers. The `shoot` function just takes a wind speed, angle of release and counterweight mass, and tells us how far the projectile got.
+
+function shoot((wind, angle, weight))
+ Trebuchet.shoot((wind, Trebuchet.deg2rad(angle), weight))[2]
+end
+
+#-
+
+shoot([0, 45, 400])
+
+# It's worth playing with these parameters to see the impact they have. How far can you throw the projectile, tweaking only the angle of release?
+
+shoot([0, 40, 400])
+
+#-
+
+# There's actually a much better way of aiming the trebuchet. Let's load up a machine learning library, Flux, and see what we can do.
+
+using Flux, Trebuchet
+using Flux.Tracker: gradient, forwarddiff
+
+# Firstly, we're going to wrap `shoot` to take a _parameter vector_ (just a list of the three numbers we're interested in). There's also a call to `forwarddiff` here, which tells Flux to differentiate the trebuchet itself using forward mode. The number of parameters is small, so forward mode will be the most efficient way to do it. Otherwise Flux defaults to reverse mode.
+
+shoot(ps) = forwarddiff(p->shoot(p...), ps)
+
+# We can get a distance as usual.
+
+shoot([0, 45, 200])
+
+# But we can also get something much more interesting: *gradients* for each of those parameters with respect to distance.
+
+gradient(x->forwarddiff(shoot, x), [0.0, 45, 200])
+
+# What does these numbers mean? The gradient tells us, very roughly, that if we increase a parameter – let's say we make wind speed 1 m/s stronger – distance will also increase by about 4 metres. Let's try that.
+Zygote.gradient(x->forwarddiff(shoot, x), [0.0, 45, 200])
+
+shoot([1, 45, 200])
+
+# Lo and behold, this is indeed about four metres further!
+
+shoot([1, 45, 200]) - shoot([0, 45, 200])
+
+# So this seems like very useful information if we're trying to aim, or maximise distance. Notice that our gradient for the release angle is negative – increasing angle will decrease distance, so in other words we should probably *decrease* angle if we want more distance. Let's try that.
+
+shoot([0, 10, 200])
+
+# Oh no, this is actually *less* far than before!
+
+#-
+
+# So if the angle is too shallow, the projectile doesn't spend enough time in the air to gain any distance before hitting the ground. But if it's too high, the projectile doesn't have enough horizontal speed even with lots of time in the air. So we'll have to find a middle ground.
+#
+# More generally, the lesson here is that the gradient only gives you limited information; it helps us take a small step towards a better aim, and we can keep iterating to get to the best possible aim. For example, we choose a starting angle:
+
+angle = 45
+shoot([0, angle, 200])
+
+# Get a gradient for `angle` alone:
+
+dangle = gradient(angle -> shoot(Tracker.collect([0, angle, 200])), angle)[1] |> Flux.data
+
+# Update the angle, using the learning rate η:
+
+η = 10
+angle += η*dangle
+
+#-
+
+shoot([0, angle, 200])
+
+# Now we just lather, rinse and repeat! Ok, maybe we should write a loop to automate this a bit.
+
+for i = 1:10
+ dangle = gradient(angle -> shoot(Tracker.collect([0, angle, 200])), angle)[1] |> Flux.data
+ angle += η*dangle
+ @show angle
+end
+shoot([0, angle, 200])
+
+# Notice how the change in the angle slows down as things converge. Turns out the best angle is about 30 degrees, and we can hit about 90 metres.
+#
+# We can make this nicely repeatable and get the best angle for any given wind speed.
+
+function best_angle(wind)
+ angle = 45
+ objective(angle) = shoot(Tracker.collect([wind, angle, 200]))
+ for i = 1:10
+ dangle = gradient(objective, angle)[1] |> Flux.data
+ angle += η*dangle
+ end
+ return angle
+end
+
+#-
+
+best_angle(0)
+
+#-
+
+best_angle(10)
+
+#-
+
+best_angle(-10)
+
+# It turns out that if the wind is on our side, we should just throw the projectile upwards and let it get blown along. If the wind is strong against us, just chuck that stone right into it.
+
+t = TrebuchetState(release_angle = deg2rad(19), wind_speed = -10)
+simulate(t)
+visualise(t)
+
+# ## Accuracy Matters
+
+#-
+
+# In optimisation terms, we just created an objective (distance) and tried to maximise that objective. Flinging boulders as far as possible has its moments, but lacks a certain subtlety. What if we instead want to hit a precise target?
+
+t = TrebuchetState()
+simulate(t)
+visualise(t, 50)
+
+# The way to do this is to state the problem in terms of maximising, or minisming, some number – the objective. In this case, an easy way to come up with an objective is to take the difference from our target (gets closer to 0 as aim gets better) and square it (so it's always positive: 0 is the lowest *and* best possible score).
+
+#-
+
+# Here's a modified `best_angle` function that takes a target and tells us the distance it acheived.
+
+η = 0.1
+function best_angle(wind, target)
+ angle = 45
+ objective(angle) = (shoot(Tracker.collect([wind, angle, 200])) - target)^2
+ for i = 1:30
+ dangle = gradient(objective, angle)[1] |> Flux.data
+ angle -= η*dangle
+ end
+ return angle, shoot([wind, angle, 200])
+end
+
+# It's pretty accurate!
+
+best_angle(0, 50)
+
+# Even when we try to push it, by making wind really strong.
+
+best_angle(-20, 35)
+
+#-
+
+t = TrebuchetState(release_angle = deg2rad(21.8), weight = 200, wind_speed = -20)
+simulate(t)
+visualise(t, 35)
+
+# ## Siege Weapon Autopilot
+
+#-
+
+# Finally, we go one level more meta by training a neural network to aim the trebuchet for us. Rather than solving a whole optimisation problem every time we want to aim, we can just ask the network for good parameters and get them in constant time.
+#
+# Here's a simple multi layer perceptron. Its input is two parameters (wind speed and target) and its output is two more (release angle and counterweight mass).
+
+model = Chain(Dense(2, 16, σ),
+ Dense(16, 64, σ),
+ Dense(64, 16, σ),
+ Dense(16, 2)) |> f64
+
+θ = params(model)
+
+function aim(wind, target)
+ angle, weight = model([wind, target])
+ angle = σ(angle)*90
+ weight = weight + 200
+ angle, weight
+end
+
+distance(wind, target) = shoot(Tracker.collect([wind, aim(wind, target)...]))
+
+# The model's initial guesses will be fairly random, and miss the mark.
+
+aim(0, 70)
+
+#-
+
+distance(0, 70)
+
+# However, just as before, we can define an objective – or loss – and get gradients.
+
+function loss(wind, target)
+ try
+ (distance(wind, target) - target)^2
+ catch e
+ # Roots.jl sometimes give convergence errors, ignore them
+ param(0)
+ end
+end
+
+loss(0, 70)
+
+# This time, though, we'll get gradients for the *model parameters*, and updating these will improve the network's accuracy. This works because we're able to differentiate the *whole program*; the backwards pass propagates errors through the trebuchet simulator and then through the ML model.
+
+dθ = gradient(θ) do
+ loss(0, 70)
+end
+dθ[model[1].W]
+
+#-
+
+DIST = (20, 100) # Maximum target distance
+SPEED = 5 # Maximum wind speed
+
+lerp(x, lo, hi) = x*(hi-lo)+lo
+
+randtarget() = (randn() * SPEED, lerp(rand(), DIST...))
+
+#-
+
+using Statistics
+
+meanloss() = mean(sqrt(loss(randtarget()...)) for i = 1:100)
+
+opt = ADAM()
+
+dataset = (randtarget() for i = 1:10_000)
+
+Flux.train!(loss, θ, dataset, opt, cb = Flux.throttle(() -> @show(meanloss()), 10))
+
+# After only a few minutes of training, we're getting solid accuracy, even on hard wind speeds and targets. You can run the training loop again to improve the accuracy even further.
+
+wind, target = -10, 50
+angle, mass = Flux.data.(aim(wind, target))
+t = TrebuchetState(release_angle = deg2rad(angle), weight = mass, wind_speed = wind)
+simulate(t)
+visualise(t, target)
+
+# Notice that aiming with a neural net in one shot is significantly faster than solving the optimisation problem; and we only have a small loss in accuracy.
+
+@time aim(wind, target)
+
+#-
+
+@time best_angle(wind, target)
+
+#-
diff --git a/Courses/Differentiable Programming/050 Forward Differentiation.jl b/Courses/Differentiable Programming/050 Forward Differentiation.jl
new file mode 100644
index 0000000..fdc0453
--- /dev/null
+++ b/Courses/Differentiable Programming/050 Forward Differentiation.jl
@@ -0,0 +1,325 @@
+module ADPackages #src
+# Some settings for running this interactively #src
+interactive_use = false #src
+plotting_off = false #src
+using BenchmarkTools #src
+if interactive_use #src
+BenchmarkTools.DEFAULT_PARAMETERS.seconds = 0.1 #src
+end #src
+
+# # Using AD packages
+#
+# While a theoretical understanding behind how automatic differentiation work
+# is interesting, in practice, being able to use existing AD packages might
+# be good enough so this is where we will start.
+# Julia has many excellent packages for AD. The purpose of this lecture
+# for you to try a few of them out and apply them to real problems like solving
+# optimization problems using AD.
+
+# ## ForwardDiff
+#
+# The most popular package for AD in Julia is [`ForwardDiff`](https://github.com/JuliaDiff/ForwardDiff.jl).
+# It uses something called *forward mode automatic differentiation* using "Dual numbers"
+# and operator overloading. Forward mode AD is efficient if the function
+# being differentiated is $\mathbb{R}^N -> \mathbb{R}^M$ with $N <= M$. In other words,
+# the dimension of the input argument should be equal or greater than the number of
+# output arguments.
+# Foroward mode AD is however not so efficient for example when `M = 1` and `N` is big, which is common in
+# e.g. machine learning. In these cases *reverse mode automatic differentiation* is
+# more efficient, and we will look at that later.
+
+# ### Derivative of scalar functions
+#
+# To have a function to start experimenting with, we define the (scalar to
+# scalar) function `f(x)` and its analytical derivative
+# `fp(x)`
+
+f(x) = exp(x) / (sin(x)^3 + cos(x)^3);
+fp(x) = exp(x) * (3sin(x) + sin(3x) + 2cos(3x)) / 2(sin(x)^3 + cos(x)^3)^2;
+
+# We can visualize the function and the derivative (here using the Plots.jl package)
+if !plotting_off #src
+using Plots
+end #src
+xs = 0.0:0.01:1.4
+if !plotting_off #src
+plot(xs, [f.(xs), fp.(xs)]; labels = ["f" "fp"])
+end #src
+
+# The only thing to do to differentiate this function using AD is to import `ForwardDiff`
+# and call the `ForwardDiff.derivative` function with the function we want to differentiate and
+# at what point we want the derivative. The function should take a scalar as an argument
+# and return a scalar and that is what our function `f` above does.
+
+import ForwardDiff
+ad_derivative = ForwardDiff.derivative(f, pi/4)
+analytical_derivative = fp(pi/4)
+@assert ad_derivative ≈ analytical_derivative #src
+@show ad_derivative - analytical_derivative;
+
+# We can see that the AD derivative is "exact" (at least exact in the sense of floating
+# point precision) to the analytical ones.
+
+# #### Performance
+#
+# It can be interesting to see what the performance of using AD vs the the performance of the
+# analytical derivative. We can use the benchmark framework [`BenchmarkTools.jl`](https://github.com/JuliaCI/BenchmarkTools.jl)
+# to help us make accurate benchmarks even for functions that execute very quickly.
+
+using BenchmarkTools
+
+@assert VERSION < v"1.1" "revise benchmarking for 1.1" #src
+
+############################################################ #src
+# TODO: THIS IS ONLY TRUE ON MASTER, THE OPTIMIZATION DOES NOT HAPPEN ON JULIA 1.0.1 #src
+# If we do some napkin math, we can see that the reported time here is completely bogus! #src
+# Making the not too terrible assumption that a CPU can do one operation per clockcycle and that #src
+# the CPU you are using has approximately 3 GHz then one instruction should take ~0.3 ns which is #src
+# much longer than the reported time here. And computing this derivative need to compute `sin`, `cos` #src
+# etc which take many CPU instructions. #src
+# We have now encounted one of hard problems when benchmarking, to make sure that the computer is actually #src
+# computing the things you want it to. What happens here is that the Julia compiler is able #src
+# to figure out that the input we gave the function (`pi/4`) is a constant and the optimizer #src
+# then figures out the result during compile time. We can see this as follows: #src
+# #src
+#g() = ForwardDiff.derivative(f, pi/4) #src
+# #src
+## Looking at the generated code for #src
+# #src
+#@code_llvm g() #src
+# #src
+# We can see that the function has been optimized to just return a single value. #src
+# The exact value looks a bit odd because it is written #src
+# but reinterpreting it as a Float64 value we can see that it is just the same #src
+# derivative as was returned from ForwardDiff: #src
+# #src
+#@show reinterpret(Float64, 0x4008D06AE62ADC94) #src
+# #src
+#@show ForwardDiff.derivative(f, pi/4) #src
+# #src
+# One way we can trick the optimizer (at least with the current version of it) to not optimized #src
+# away the computation #src
+# is to encapsulate our value in a container like a [`Ref`](https://docs.julialang.org/en/v1/base/c/#Core.Ref) #src
+# #src
+##################################################################################### #src
+
+# A function can be benchmarked by prepending the call with `@btime`.
+# This will run the function multiple time and collect statistics on the
+# time it took to execute the function:
+
+println("Original function")
+@btime f(pi/4);
+println("AD derivative")
+@btime ForwardDiff.derivative(f, pi/4);
+println("Analytical derivative")
+@btime fp(pi/4);
+
+# We can here see that for the way we implemented the analytical derivative there is virtually no
+# performance difference between the AD version and the analyitical version.
+# However, it should be noted that the current version of the analytical function is not the
+# one with the best performance. Feel free to try to improve it.
+
+# A nice thing about AD is that you don't have to spend time making sure that
+# not only is the derivative correct, but that it is also efficiently computed.
+# By using AD, you get "free" performance for the derivative by optimizing the function itself.
+
+# #### Second derivatives
+#
+# For scalar functions `ForwardDiff` does not come with built in functionality for computing
+# the second derivative. It is, fortunately, very easy to create such a function ourselves.
+# The second derivative is just the derivative of the derivative which we can implement as:
+
+derivative2(f, x) = ForwardDiff.derivative(z -> ForwardDiff.derivative(f, z), x)
+
+@assert derivative2(f, pi/4) ≈ -6.203532787672101 #src
+@show derivative2(f, pi/4);
+
+# Here, we created an anonymous function that computes derivatives of `f`,
+# `z -> ForwardDiff.derivative(f, z)`, and then we used that as the input
+# derivative for another `ForwardDiff.derivative` call. The derivative
+# of the derivative gives the second derivative. Simple!
+# Feel free to compute the second derivative by hand and verify that the result
+# is correct (and appreciate that AD savees you from doing it in the first place).
+# The correct analytical result is `-2sqrt(2) * exp(pi/4)`.
+
+# #### Differentiating functions with parameters
+#
+# It is common to have a function that depends on some parameters that are considered
+# fixed in the context of differentiation.
+# An example of this might be the function `g` (and its derivative `gp) below:
+
+g(x, a) = (x - a)^3
+gp(x, a) = 3*(x - a)^2
+
+# Here, `g` has the parameter `a` and we want to take the derivative with respect to `x`.
+# Recall that `ForwardDiff.derivative` needs a function that takes only one
+# argument, but `g` above takes two arguments, so it clearly cannot be used directly.
+# The solution is to create what is typically called a "closure", which is a new function
+# that "closes" over some parameter space.
+# For example, consider:
+
+const a = 3
+g2(x) = g(x, a)
+
+@show (2 - a)^3
+@show g2(2);
+
+# We now have a new function `g2` which takes only one argument (`x`) and "closes" over the
+# variable `a`. We can now differentiate `g2`.
+
+@show ForwardDiff.derivative(g2, 2.0)
+@show gp(2.0, 3);
+
+# It is possible to write this a bit more succintly using an anonymous function
+
+ForwardDiff.derivative(x -> g(x, a), 2.0)
+
+# ## Gradients
+#
+# If our function takes a vector as input and returns a scalar, the derivative
+# is a vector (called a gradient) which gives the sensitivity of the output with respect to
+# all inputs. A quite common function to use in examples involving optimization
+# is the [Rosenbrock function](https://en.wikipedia.org/wiki/Rosenbrock_function), defined as:
+
+function rosenbrock(x)
+ a = one(eltype(x))
+ b = 100 * a
+ result = zero(eltype(x))
+ for i in 1:length(x)-1
+ result += (a - x[i])^2 + b*(x[i+1] - x[i]^2)^2
+ end
+ return result
+end
+
+# Evaluating `rosenbrock` with a vector input indeed gives a scalar back.
+
+rosenbrock([1.0, 0.5, 2.0])
+@assert rosenbrock([1.0, 0.5, 2.0]) == 331.5 #src
+
+# We can see how this function looks by plotting it
+
+xs = -3:0.1:3
+ys = -3:0.1:3
+zs = [rosenbrock([x, y]) for x in xs, y in ys]
+if !plotting_off #src
+contour(xs, ys, zs; levels=40)
+end #src
+
+# Evaluating the `gradient` is almost as simple as the `derivative`:
+
+x_vec = [1.0, 2.0]
+ForwardDiff.gradient(rosenbrock, x_vec)
+
+# ### Performance
+#
+# When evaluating the gradient we are dealing with `Vector`s which require allocation
+# so there are a few extra performance considerations for `gradient` compared to `derivative`
+
+# #### Preallocating output
+#
+# `ForwardDiff.gradient` returns a `Vector` which needs to be allocated. We can preallocate
+# this so `ForwardDiff` doesn't need to to it by itself.
+
+z_vec = similar(x_vec)
+ForwardDiff.gradient!(z_vec, rosenbrock, x_vec)
+@show z_vec;
+
+# The result was now stored in the, by us, allocated `z_vec`. We can check the performance difference
+
+println("No preallocation")
+@btime ForwardDiff.gradient(rosenbrock, $x_vec)
+println("No preallocation")
+@btime ForwardDiff.gradient!($z_vec,rosenbrock, $x_vec)
+
+# We can see that we do one allocation less and that performance is significantly
+# improved.
+
+# #### Preallocating internal datastructures
+#
+# Even though we preallocated the output vector there are some
+# internal data structures used by ForwardDiff that we in addition can preallocate
+# This is done by creating a `GradientConfig`:
+
+gradient_cache = ForwardDiff.GradientConfig(rosenbrock, x_vec)
+@btime ForwardDiff.gradient!($z_vec, rosenbrock, $x_vec, $gradient_cache);
+
+# Which as we can see further increase performance.
+# All of this is documented in the ForwardDiff manual so the takehome message is
+# to read the manual of the package one uses. There are often valuable information
+# there that could (like in this case) significantly improve performance.
+
+# ### Solving optimization using ForwardDiff
+#
+# [`Optim`](https://github.com/JuliaNLSolvers/Optim.jl) is a package that has many useful optimization routines.
+# If you can provide the gradient (and even sec) you get access to optimization routines that can
+# have significantly better performance. Lets use first try to just optimize the function without
+# using any gradient information. This will default to using the
+# [Nelder-Mead method](https://en.wikipedia.org/wiki/Nelder%E2%80%93Mead_method).
+# We also stick a `@btime` in there to see how long time the optimization routine take.
+using Random; Random.seed!(1234) #src
+using Optim
+x0 = zeros(10)
+@btime optimize(rosenbrock, x0)
+
+# We can see that we require approximately 620 evaluations of `rosenbrock` before
+# a minimum was found. Let's try giving `Optim` the gradient as well:
+#
+using Random; Random.seed!(1234) #src
+const gradient_cache_optim = ForwardDiff.GradientConfig(rosenbrock, x0)
+const rosenbrock_gradient! = (z, x) -> ForwardDiff.gradient!(z,rosenbrock, x, gradient_cache_optim)
+
+@btime optimize(rosenbrock, rosenbrock_gradient!, x0)
+
+# Now we only called the function 92 times (and in addition the gradient 153 times)
+# Looking at the time taken this was almost a 3x speedup. The minimum we found had a
+# was also significantly smaller than when we used Nelder-Mead
+
+# ## Hessians
+# It is also possible to compute Hessians (second derivative) in a very similar way to `gradient`
+
+ForwardDiff.hessian(rosenbrock, [1.0, 2.0])
+
+# We leave out the details for `ForwardDiff.hessian` here and instead refer to the [`ForwardDiff.hessian`](http://www.juliadiff.org/ForwardDiff.jl/stable/user/api.html#Hessians-of-f(x::AbstractArray)::Real-1)
+# documentation.
+
+# ## Jacobians
+#
+# If our function takes a vector as argument and returns a vector, the derivative is a `Matrix` which
+# is known as the Jacobian. This derivative is useful when we want to solve a nonlinear system of
+# equations.
+# Let's consider the following function that slightly resembles the `rosenbrock` function:
+
+function rosenbrock_vector(x)
+ return [
+ 1 - x[1],
+ 10(x[2]-x[1]^2)
+ ]
+end
+
+# Indeed calling this function with a vector argument returns a vector:
+
+rosenbrock_vector([1.0, 0.5])
+
+# By now, we should be quite familiar with the ForwarDiff interface and you might
+# even guess how we should compute the Jacobian:
+
+ForwardDiff.jacobian(rosenbrock_vector, [1.0, 0.5])
+
+# The Jacobian functionality could be used for example in [`NLsolve.jl`](https://github.com/JuliaNLSolvers/NLsolve.jl),
+# which is a nonlinear equation solver.
+
+# ### Summary `ForwardDiff`
+# This should get you started with using `ForwardDiff`. If your functions do not have too big vectors as
+# input arguments, the performance should be good. It will likely not beat a carefully tuned
+# analytical implementaion of the derivative but it is oftan that from a productivity point of view
+# it is worth using AD.
+
+# ## Revisediff
+#
+# ForwardDiff is using what is known as forward mode differentiation.
+# If the number of input parameters is large and the output is just a scalar
+# then reverse mode differentation is likely more effective.
+#
+# TODO..
+
+end #src
diff --git a/Courses/Differentiable Programming/060 Reverse Differentiation.jl b/Courses/Differentiable Programming/060 Reverse Differentiation.jl
new file mode 100644
index 0000000..e69de29
diff --git a/Courses/Differentiable Programming/Manifest.toml b/Courses/Differentiable Programming/Manifest.toml
new file mode 100644
index 0000000..9b3c023
--- /dev/null
+++ b/Courses/Differentiable Programming/Manifest.toml
@@ -0,0 +1,872 @@
+# This file is machine-generated - editing it directly is not advised
+
+[[AbstractTrees]]
+deps = ["Markdown", "Test"]
+git-tree-sha1 = "6621d9645702c1c4e6970cc6a3eae440c768000b"
+uuid = "1520ce14-60c1-5f80-bbc7-55ef81b5835c"
+version = "0.2.1"
+
+[[Adapt]]
+deps = ["LinearAlgebra", "Test"]
+git-tree-sha1 = "53d8fec4f662088c1202530e338a11a919407f3b"
+uuid = "79e6a3ab-5dfb-504d-930d-738a2a938a0e"
+version = "0.4.2"
+
+[[Arpack]]
+deps = ["BinaryProvider", "Libdl", "LinearAlgebra"]
+git-tree-sha1 = "07a2c077bdd4b6d23a40342a8a108e2ee5e58ab6"
+uuid = "7d9fca2a-8960-54d3-9f78-7d1dccf2cb97"
+version = "0.3.1"
+
+[[ArrayInterface]]
+deps = ["Requires", "Test"]
+git-tree-sha1 = "6a1a371393e56f5e8d5657fe4da4b11aea0bfbae"
+uuid = "4fba245c-0d91-5ea0-9b3e-6abc04ee57a9"
+version = "0.1.1"
+
+[[AssetRegistry]]
+deps = ["Distributed", "JSON", "Pidfile", "SHA", "Test"]
+git-tree-sha1 = "b25e88db7944f98789130d7b503276bc34bc098e"
+uuid = "bf4720bc-e11a-5d0c-854e-bdca1663c893"
+version = "0.1.0"
+
+[[BandedMatrices]]
+deps = ["FillArrays", "LazyArrays", "LinearAlgebra", "MatrixFactorizations", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "dd74592d0952af59b97e12d6f69bfc9cc3a79614"
+uuid = "aae01518-5342-5314-be14-df237901396f"
+version = "0.9.2"
+
+[[Base64]]
+uuid = "2a0f44e3-6c83-55bd-87e4-b1978d98bd5f"
+
+[[BenchmarkTools]]
+deps = ["JSON", "Printf", "Statistics", "Test"]
+git-tree-sha1 = "5d1dd8577643ba9014574cd40d9c028cd5e4b85a"
+uuid = "6e4b80f9-dd63-53aa-95a3-0cdb28fa8baf"
+version = "0.4.2"
+
+[[BinDeps]]
+deps = ["Compat", "Libdl", "SHA", "URIParser"]
+git-tree-sha1 = "12093ca6cdd0ee547c39b1870e0c9c3f154d9ca9"
+uuid = "9e28174c-4ba2-5203-b857-d8d62c4213ee"
+version = "0.8.10"
+
+[[BinaryProvider]]
+deps = ["Libdl", "Logging", "SHA"]
+git-tree-sha1 = "8153fd64131cd00a79544bb23788877741f627bb"
+uuid = "b99e7846-7c00-51b0-8f62-c81ae34c0232"
+version = "0.5.5"
+
+[[BoundaryValueDiffEq]]
+deps = ["BandedMatrices", "DiffEqBase", "DiffEqDiffTools", "ForwardDiff", "LinearAlgebra", "NLsolve", "Reexport", "SparseArrays", "Test"]
+git-tree-sha1 = "0f4a4f86ae63671efd9b41de9dea8ad993f2daad"
+uuid = "764a87c0-6b3e-53db-9096-fe964310641d"
+version = "2.2.3"
+
+[[CSTParser]]
+deps = ["Tokenize"]
+git-tree-sha1 = "376a39f1862000442011390f1edf5e7f4dcc7142"
+uuid = "00ebfdb7-1f24-5e51-bd34-a7502290713f"
+version = "0.6.0"
+
+[[CSV]]
+deps = ["CategoricalArrays", "DataFrames", "Dates", "Mmap", "Parsers", "PooledArrays", "Profile", "Tables", "Unicode", "WeakRefStrings"]
+git-tree-sha1 = "078801ccf5a644df31cef99c9add46107b94aba5"
+uuid = "336ed68f-0bac-5ca0-87d4-7b16caf5d00b"
+version = "0.5.6"
+
+[[Calculus]]
+deps = ["Compat"]
+git-tree-sha1 = "f60954495a7afcee4136f78d1d60350abd37a409"
+uuid = "49dc2e85-a5d0-5ad3-a950-438e2897f1b9"
+version = "0.4.1"
+
+[[CategoricalArrays]]
+deps = ["Compat", "Future", "JSON", "Missings", "Printf", "Reexport"]
+git-tree-sha1 = "26601961df6afacdd16d67c1eec6cfe75e5ae9ab"
+uuid = "324d7699-5711-5eae-9e2f-1d82baa6b597"
+version = "0.5.4"
+
+[[CodecZlib]]
+deps = ["BinaryProvider", "Libdl", "Test", "TranscodingStreams"]
+git-tree-sha1 = "36bbf5374c661054d41410dc53ff752972583b9b"
+uuid = "944b1d66-785c-5afd-91f1-9de20f533193"
+version = "0.5.2"
+
+[[ColorTypes]]
+deps = ["FixedPointNumbers", "Random"]
+git-tree-sha1 = "10050a24b09e8e41b951e9976b109871ce98d965"
+uuid = "3da002f7-5984-5a60-b8a6-cbb66c0b333f"
+version = "0.8.0"
+
+[[Colors]]
+deps = ["ColorTypes", "FixedPointNumbers", "InteractiveUtils", "Printf", "Reexport", "Test"]
+git-tree-sha1 = "9f0a0210450acb91c730b730a994f8eef1d3d543"
+uuid = "5ae59095-9a9b-59fe-a467-6f913c188581"
+version = "0.9.5"
+
+[[CommonSubexpressions]]
+deps = ["Test"]
+git-tree-sha1 = "efdaf19ab11c7889334ca247ff4c9f7c322817b0"
+uuid = "bbf7d656-a473-5ed7-a52c-81e309532950"
+version = "0.2.0"
+
+[[Compat]]
+deps = ["Base64", "Dates", "DelimitedFiles", "Distributed", "InteractiveUtils", "LibGit2", "Libdl", "LinearAlgebra", "Markdown", "Mmap", "Pkg", "Printf", "REPL", "Random", "Serialization", "SharedArrays", "Sockets", "SparseArrays", "Statistics", "Test", "UUIDs", "Unicode"]
+git-tree-sha1 = "84aa74986c5b9b898b0d1acaf3258741ee64754f"
+uuid = "34da2185-b29b-5c13-b0c7-acf172513d20"
+version = "2.1.0"
+
+[[Contour]]
+deps = ["LinearAlgebra", "StaticArrays", "Test"]
+git-tree-sha1 = "b974e164358fea753ef853ce7bad97afec15bb80"
+uuid = "d38c429a-6771-53c6-b99e-75d170b6e991"
+version = "0.5.1"
+
+[[Crayons]]
+deps = ["Test"]
+git-tree-sha1 = "f621b8ef51fd2004c7cf157ea47f027fdeac5523"
+uuid = "a8cc5b0e-0ffa-5ad4-8c14-923d3ee1735f"
+version = "4.0.0"
+
+[[DataFrames]]
+deps = ["CategoricalArrays", "Compat", "IteratorInterfaceExtensions", "Missings", "PooledArrays", "Printf", "REPL", "Reexport", "SortingAlgorithms", "Statistics", "StatsBase", "TableTraits", "Tables", "Unicode"]
+git-tree-sha1 = "7c0f86a01be0f77cc7f3f9096ed875f1217487e1"
+uuid = "a93c6f00-e57d-5684-b7b6-d8193f3e46c0"
+version = "0.18.4"
+
+[[DataStructures]]
+deps = ["InteractiveUtils", "OrderedCollections", "Random", "Serialization", "Test"]
+git-tree-sha1 = "ca971f03e146cf144a9e2f2ce59674f5bf0e8038"
+uuid = "864edb3b-99cc-5e75-8d2d-829cb0a9cfe8"
+version = "0.15.0"
+
+[[DataValueInterfaces]]
+git-tree-sha1 = "bfc1187b79289637fa0ef6d4436ebdfe6905cbd6"
+uuid = "e2d170a0-9d28-54be-80f0-106bbe20a464"
+version = "1.0.0"
+
+[[Dates]]
+deps = ["Printf"]
+uuid = "ade2ca70-3891-5945-98fb-dc099432e06a"
+
+[[DelayDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "ForwardDiff", "MuladdMacro", "NLSolversBase", "OrdinaryDiffEq", "RecursiveArrayTools", "Reexport", "Roots"]
+git-tree-sha1 = "d933682653f8c3c922592d75e50b5a30689ede6d"
+uuid = "bcd4f6db-9728-5f36-b5f7-82caef46ccdb"
+version = "5.4.1"
+
+[[DelimitedFiles]]
+deps = ["Mmap"]
+uuid = "8bb1440f-4735-579b-a4ab-409b98df4dab"
+
+[[DiffEqBase]]
+deps = ["Compat", "Distributed", "DocStringExtensions", "FunctionWrappers", "IterativeSolvers", "IteratorInterfaceExtensions", "LinearAlgebra", "MuladdMacro", "Parameters", "RecipesBase", "RecursiveArrayTools", "RecursiveFactorization", "Requires", "Roots", "SparseArrays", "StaticArrays", "Statistics", "SuiteSparse", "TableTraits", "TreeViews"]
+git-tree-sha1 = "3c08441014d2e1bad515df5443dd2d0ba379888c"
+uuid = "2b5f629d-d688-5b77-993f-72d75c75574e"
+version = "5.12.0"
+
+[[DiffEqCallbacks]]
+deps = ["DataStructures", "DiffEqBase", "LinearAlgebra", "OrdinaryDiffEq", "RecipesBase", "RecursiveArrayTools", "StaticArrays", "Test"]
+git-tree-sha1 = "027a13f010f2a93b2df725b7f6202590ce6f559d"
+uuid = "459566f4-90b8-5000-8ac3-15dfb0a30def"
+version = "2.5.2"
+
+[[DiffEqDiffTools]]
+deps = ["LinearAlgebra", "SparseArrays", "StaticArrays"]
+git-tree-sha1 = "2d4f49c1839c1f30e4820400d8c109c6b16e869a"
+uuid = "01453d9d-ee7c-5054-8395-0335cb756afa"
+version = "0.13.0"
+
+[[DiffEqFinancial]]
+deps = ["DiffEqBase", "DiffEqNoiseProcess", "LinearAlgebra", "Markdown", "RandomNumbers", "Test"]
+git-tree-sha1 = "f250512b982b771f6bdb3df05b89df314f2c2580"
+uuid = "5a0ffddc-d203-54b0-88ba-2c03c0fc2e67"
+version = "2.1.0"
+
+[[DiffEqFlux]]
+deps = ["Adapt", "DiffEqBase", "DiffEqSensitivity", "DiffResults", "Flux", "ForwardDiff", "RecursiveArrayTools", "Requires"]
+git-tree-sha1 = "1c311e6a4f14c70c7ea33482db9856392c4b6b80"
+uuid = "aae7a2af-3d4f-5e19-a356-7da93b79d9d0"
+version = "0.5.0"
+
+[[DiffEqJump]]
+deps = ["Compat", "DataStructures", "DiffEqBase", "FunctionWrappers", "LinearAlgebra", "Parameters", "PoissonRandom", "Random", "RandomNumbers", "RecursiveArrayTools", "Statistics", "Test", "TreeViews"]
+git-tree-sha1 = "784b979eeca8e9586aea9e63edbdcf5573bf9449"
+uuid = "c894b116-72e5-5b58-be3c-e6d8d4ac2b12"
+version = "6.1.1"
+
+[[DiffEqMonteCarlo]]
+deps = ["DiffEqBase", "Distributed", "RecursiveArrayTools", "StaticArrays", "Statistics"]
+git-tree-sha1 = "edffd3e114b5c2cad15e7790db6d82f69e3f42ae"
+uuid = "78ddff82-25fc-5f2b-89aa-309469cbf16f"
+version = "0.15.1"
+
+[[DiffEqNoiseProcess]]
+deps = ["DataStructures", "DiffEqBase", "LinearAlgebra", "Random", "RandomNumbers", "RecipesBase", "RecursiveArrayTools", "Requires", "ResettableStacks", "StaticArrays", "Statistics"]
+git-tree-sha1 = "f5333c0aa6208680e48cd24ae6f759c262a1cf85"
+uuid = "77a26b50-5914-5dd7-bc55-306e6241c503"
+version = "3.3.1"
+
+[[DiffEqOperators]]
+deps = ["DiffEqBase", "ForwardDiff", "LinearAlgebra", "SparseArrays", "StaticArrays", "SuiteSparse"]
+git-tree-sha1 = "2884a79a72aac38347b247615ac42eda41aa36e0"
+uuid = "9fdde737-9c7f-55bf-ade8-46b3f136cc48"
+version = "3.5.0"
+
+[[DiffEqPhysics]]
+deps = ["Dates", "DiffEqBase", "DiffEqCallbacks", "ForwardDiff", "LinearAlgebra", "Printf", "Random", "RecipesBase", "RecursiveArrayTools", "Reexport", "StaticArrays", "Test"]
+git-tree-sha1 = "d3dbc53318a6477f496ae2347db98c3ded36c486"
+uuid = "055956cb-9e8b-5191-98cc-73ae4a59e68a"
+version = "3.1.0"
+
+[[DiffEqSensitivity]]
+deps = ["DataFrames", "DiffEqBase", "DiffEqCallbacks", "DiffEqDiffTools", "Flux", "ForwardDiff", "GLM", "LinearAlgebra", "QuadGK", "RecursiveArrayTools", "Statistics"]
+git-tree-sha1 = "09c964dc242f295180dd99d89fb2f259927029ef"
+uuid = "41bf760c-e81c-5289-8e54-58b1f1f8abe2"
+version = "3.2.4"
+
+[[DiffResults]]
+deps = ["Compat", "StaticArrays"]
+git-tree-sha1 = "34a4a1e8be7bc99bc9c611b895b5baf37a80584c"
+uuid = "163ba53b-c6d8-5494-b064-1a9d43ac40c5"
+version = "0.0.4"
+
+[[DiffRules]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "dc0869fb2f5b23466b32ea799bd82c76480167f7"
+uuid = "b552c78f-8df3-52c6-915a-8e097449b14b"
+version = "0.0.10"
+
+[[DifferentialEquations]]
+deps = ["BoundaryValueDiffEq", "DelayDiffEq", "DiffEqBase", "DiffEqCallbacks", "DiffEqFinancial", "DiffEqJump", "DiffEqMonteCarlo", "DiffEqNoiseProcess", "DiffEqPhysics", "DimensionalPlotRecipes", "LinearAlgebra", "MultiScaleArrays", "OrdinaryDiffEq", "Random", "RecursiveArrayTools", "Reexport", "SteadyStateDiffEq", "StochasticDiffEq", "Sundials"]
+git-tree-sha1 = "e5b3ca6afe2a064bdfecba483999ee75d81750c6"
+uuid = "0c46a032-eb83-5123-abaf-570d42b7fbaa"
+version = "6.4.0"
+
+[[DimensionalPlotRecipes]]
+deps = ["LinearAlgebra", "RecipesBase", "Test"]
+git-tree-sha1 = "d348688f9a3d02c24455327231c450c272b7401c"
+uuid = "c619ae07-58cd-5f6d-b883-8f17bd6a98f9"
+version = "0.2.0"
+
+[[Distances]]
+deps = ["LinearAlgebra", "Printf", "Random", "Statistics", "Test"]
+git-tree-sha1 = "a135c7c062023051953141da8437ed74f89d767a"
+uuid = "b4f34e82-e78d-54a5-968a-f98e89d6e8f7"
+version = "0.8.0"
+
+[[Distributed]]
+deps = ["Random", "Serialization", "Sockets"]
+uuid = "8ba89e20-285c-5b6f-9357-94700520ee1b"
+
+[[Distributions]]
+deps = ["LinearAlgebra", "PDMats", "Printf", "QuadGK", "Random", "SpecialFunctions", "Statistics", "StatsBase", "StatsFuns"]
+git-tree-sha1 = "56a158bc0abe4af5d4027af2275fde484261ca6d"
+uuid = "31c24e10-a181-5473-b8eb-7969acd0382f"
+version = "0.19.2"
+
+[[DocStringExtensions]]
+deps = ["LibGit2", "Markdown", "Pkg", "Test"]
+git-tree-sha1 = "0513f1a8991e9d83255e0140aace0d0fc4486600"
+uuid = "ffbed154-4ef7-542d-bbb7-c09d3a79fcae"
+version = "0.8.0"
+
+[[ExponentialUtilities]]
+deps = ["LinearAlgebra", "Printf", "SparseArrays"]
+git-tree-sha1 = "85e1ce16aa9b98793df704e17e7a0ceadefe404f"
+uuid = "d4d017d3-3776-5f7e-afef-a10c40355c18"
+version = "1.5.1"
+
+[[FileWatching]]
+uuid = "7b1f6079-737a-58dc-b8bc-7a2ca5c1b5ee"
+
+[[FillArrays]]
+deps = ["LinearAlgebra", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "9ab8f76758cbabba8d7f103c51dce7f73fcf8e92"
+uuid = "1a297f60-69ca-5386-bcde-b61e274b549b"
+version = "0.6.3"
+
+[[FixedPointNumbers]]
+git-tree-sha1 = "d14a6fa5890ea3a7e5dcab6811114f132fec2b4b"
+uuid = "53c48c17-4a7d-5ca2-90c5-79b7896eea93"
+version = "0.6.1"
+
+[[Flux]]
+deps = ["AbstractTrees", "Adapt", "CodecZlib", "Colors", "DelimitedFiles", "Juno", "LinearAlgebra", "MacroTools", "NNlib", "Pkg", "Printf", "Random", "Reexport", "Requires", "SHA", "Statistics", "StatsBase", "Tracker", "ZipFile"]
+git-tree-sha1 = "08212989c2856f95f90709ea5fd824bd27b34514"
+uuid = "587475ba-b771-5e3f-ad9e-33799f191a9c"
+version = "0.8.3"
+
+[[ForwardDiff]]
+deps = ["CommonSubexpressions", "DiffResults", "DiffRules", "InteractiveUtils", "LinearAlgebra", "NaNMath", "Random", "SparseArrays", "SpecialFunctions", "StaticArrays", "Test"]
+git-tree-sha1 = "4c4d727f1b7e0092134fabfab6396b8945c1ea5b"
+repo-rev = "master"
+repo-url = "https://github.com/JuliaDiff/ForwardDiff.jl.git"
+uuid = "f6369f11-7733-5829-9624-2563aa707210"
+version = "0.10.3+"
+
+[[FunctionWrappers]]
+deps = ["Compat"]
+git-tree-sha1 = "49bf793ebd37db5adaa7ac1eae96c2c97ec86db5"
+uuid = "069b7b12-0de2-55c6-9aab-29f3d0a68a2e"
+version = "1.0.0"
+
+[[FunctionalCollections]]
+deps = ["Test"]
+git-tree-sha1 = "04cb9cfaa6ba5311973994fe3496ddec19b6292a"
+uuid = "de31a74c-ac4f-5751-b3fd-e18cd04993ca"
+version = "0.5.0"
+
+[[Future]]
+deps = ["Random"]
+uuid = "9fa8497b-333b-5362-9e8d-4d0656e87820"
+
+[[GLM]]
+deps = ["Distributions", "LinearAlgebra", "Printf", "Random", "Reexport", "SparseArrays", "SpecialFunctions", "Statistics", "StatsBase", "StatsFuns", "StatsModels"]
+git-tree-sha1 = "bb918f52a8e2131857ddac319033610bb3be35a4"
+uuid = "38e38edf-8417-5370-95a0-9cbb8c7f171a"
+version = "1.3.0"
+
+[[GR]]
+deps = ["Base64", "DelimitedFiles", "LinearAlgebra", "Pkg", "Printf", "Random", "Serialization", "Sockets", "Test"]
+git-tree-sha1 = "9dff2d231311da78648abfa3287e3458a578d2f8"
+uuid = "28b8d3ca-fb5f-59d9-8090-bfdbd6d07a71"
+version = "0.40.0"
+
+[[GenericSVD]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "8aa93c3f3d81562a8962047eafcc5712af0a0f59"
+uuid = "01680d73-4ee2-5a08-a1aa-533608c188bb"
+version = "0.2.1"
+
+[[GeometryTypes]]
+deps = ["ColorTypes", "FixedPointNumbers", "IterTools", "LinearAlgebra", "StaticArrays"]
+git-tree-sha1 = "2b0bfb379a54bdfcd2942f388f7d045f8952373d"
+uuid = "4d00f742-c7ba-57c2-abde-4428a4b178cb"
+version = "0.7.5"
+
+[[HTTP]]
+deps = ["Base64", "Dates", "IniFile", "MbedTLS", "Sockets"]
+git-tree-sha1 = "6e59e7ec3c71eda9e0261c98896da5d3d008fa7d"
+uuid = "cd3eb016-35fb-5094-929b-558a96fad6f3"
+version = "0.8.3"
+
+[[IRTools]]
+deps = ["InteractiveUtils", "MacroTools", "Test"]
+git-tree-sha1 = "a9b1fc7745ae4745a634bbb6d1cb7fd64e37248a"
+uuid = "7869d1d1-7146-5819-86e3-90919afe41df"
+version = "0.2.2"
+
+[[IniFile]]
+deps = ["Test"]
+git-tree-sha1 = "098e4d2c533924c921f9f9847274f2ad89e018b8"
+uuid = "83e8ac13-25f8-5344-8a64-a9f2b223428f"
+version = "0.5.0"
+
+[[InteractiveUtils]]
+deps = ["Markdown"]
+uuid = "b77e0a4c-d291-57a0-90e8-8db25a27a240"
+
+[[IterTools]]
+deps = ["SparseArrays", "Test"]
+git-tree-sha1 = "79246285c43602384e6f1943b3554042a3712056"
+uuid = "c8e1da08-722c-5040-9ed9-7db0dc04731e"
+version = "1.1.1"
+
+[[IterativeSolvers]]
+deps = ["LinearAlgebra", "Printf", "Random", "RecipesBase", "SparseArrays", "Test"]
+git-tree-sha1 = "5687f68018b4f14c0da54d402bb23eecaec17f37"
+uuid = "42fd0dbc-a981-5370-80f2-aaf504508153"
+version = "0.8.1"
+
+[[IteratorInterfaceExtensions]]
+git-tree-sha1 = "a3f24677c21f5bbe9d2a714f95dcd58337fb2856"
+uuid = "82899510-4779-5014-852e-03e436cf321d"
+version = "1.0.0"
+
+[[JSExpr]]
+deps = ["JSON", "MacroTools", "Observables", "Test", "WebIO"]
+git-tree-sha1 = "013bc2143a2e84ea489365cf30db3407deb540c2"
+uuid = "97c1335a-c9c5-57fe-bc5d-ec35cebe8660"
+version = "0.5.0"
+
+[[JSON]]
+deps = ["Dates", "Distributed", "Mmap", "Sockets", "Test", "Unicode"]
+git-tree-sha1 = "1f7a25b53ec67f5e9422f1f551ee216503f4a0fa"
+uuid = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
+version = "0.20.0"
+
+[[Juno]]
+deps = ["Base64", "Logging", "Media", "Profile", "Test"]
+git-tree-sha1 = "4e4a8d43aa7ecec66cadaf311fbd1e5c9d7b9175"
+uuid = "e5e0dc1b-0480-54bc-9374-aad01c23163d"
+version = "0.7.0"
+
+[[LazyArrays]]
+deps = ["FillArrays", "LinearAlgebra", "MacroTools", "StaticArrays", "Test"]
+git-tree-sha1 = "5eec856c454496abe8f4504227fcc187205a502a"
+uuid = "5078a376-72f3-5289-bfd5-ec5146d43c02"
+version = "0.9.0"
+
+[[LibGit2]]
+uuid = "76f85450-5226-5b5a-8eaa-529ad045b433"
+
+[[Libdl]]
+uuid = "8f399da3-3557-5675-b5ff-fb832c97cbdb"
+
+[[LineSearches]]
+deps = ["LinearAlgebra", "NLSolversBase", "NaNMath", "Parameters", "Printf", "Test"]
+git-tree-sha1 = "54eb90e8dbe745d617c78dee1d6ae95c7f6f5779"
+uuid = "d3d80556-e9d4-5f37-9878-2ab0fcc64255"
+version = "7.0.1"
+
+[[LinearAlgebra]]
+deps = ["Libdl"]
+uuid = "37e2e46d-f89d-539d-b4ee-838fcccc9c8e"
+
+[[Literate]]
+deps = ["Base64", "JSON", "REPL", "Test"]
+git-tree-sha1 = "021e2e3106713e22a7f3769ebf9f2f4469670444"
+uuid = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
+version = "1.1.0"
+
+[[Logging]]
+uuid = "56ddb016-857b-54e1-b83d-db4d58db5568"
+
+[[MacroTools]]
+deps = ["CSTParser", "Compat", "DataStructures", "Test"]
+git-tree-sha1 = "daecd9e452f38297c686eba90dba2a6d5da52162"
+uuid = "1914dd2f-81c6-5fcd-8719-6d5c9610ff09"
+version = "0.5.0"
+
+[[Markdown]]
+deps = ["Base64"]
+uuid = "d6f4376e-aef5-505a-96c1-9c027394607a"
+
+[[MatrixFactorizations]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "cebc71d929a846dda61400f1cf3ba69c7e75fa63"
+uuid = "a3b82374-2e81-5b9e-98ce-41277c0e4c87"
+version = "0.0.4"
+
+[[MbedTLS]]
+deps = ["BinaryProvider", "Dates", "Libdl", "Random", "Sockets"]
+git-tree-sha1 = "85f5947b53c8cfd53ccfa3f4abae31faa22c2181"
+uuid = "739be429-bea8-5141-9913-cc70e7f3736d"
+version = "0.7.0"
+
+[[Measures]]
+deps = ["Test"]
+git-tree-sha1 = "ddfd6d13e330beacdde2c80de27c1c671945e7d9"
+uuid = "442fdcdd-2543-5da2-b0f3-8c86c306513e"
+version = "0.3.0"
+
+[[Media]]
+deps = ["MacroTools", "Test"]
+git-tree-sha1 = "75a54abd10709c01f1b86b84ec225d26e840ed58"
+uuid = "e89f7d12-3494-54d1-8411-f7d8b9ae1f27"
+version = "0.5.0"
+
+[[Missings]]
+deps = ["SparseArrays", "Test"]
+git-tree-sha1 = "f0719736664b4358aa9ec173077d4285775f8007"
+uuid = "e1d29d7a-bbdc-5cf2-9ac0-f12de2c33e28"
+version = "0.4.1"
+
+[[Mmap]]
+uuid = "a63ad114-7e13-5084-954f-fe012c677804"
+
+[[MuladdMacro]]
+deps = ["MacroTools", "Test"]
+git-tree-sha1 = "41e6e7c4b448afeaddaac7f496b414854f83b848"
+uuid = "46d2c3a1-f734-5fdb-9937-b9b9aeba4221"
+version = "0.2.1"
+
+[[MultiScaleArrays]]
+deps = ["DiffEqBase", "LinearAlgebra", "RecursiveArrayTools", "Statistics", "StochasticDiffEq", "Test", "TreeViews"]
+git-tree-sha1 = "4220ceea71186db2bb45cb817984c99e563f3662"
+uuid = "f9640e96-87f6-5992-9c3b-0743c6a49ffa"
+version = "1.4.0"
+
+[[NLSolversBase]]
+deps = ["Calculus", "DiffEqDiffTools", "DiffResults", "Distributed", "ForwardDiff", "LinearAlgebra", "Random", "SparseArrays", "Test"]
+git-tree-sha1 = "0c6f0e7f2178f78239cfb75310359eed10f2cacb"
+uuid = "d41bc354-129a-5804-8e4c-c37616107c6c"
+version = "7.3.1"
+
+[[NLsolve]]
+deps = ["DiffEqDiffTools", "Distances", "ForwardDiff", "LineSearches", "LinearAlgebra", "NLSolversBase", "Printf", "Random", "Reexport", "SparseArrays", "Test"]
+git-tree-sha1 = "413e54f04a4cbe9804089794eec6b06b2a43bc47"
+uuid = "2774e3e8-f4cf-5e23-947b-6d7e65073b56"
+version = "4.0.0"
+
+[[NNlib]]
+deps = ["Libdl", "LinearAlgebra", "Requires", "Statistics", "TimerOutputs"]
+git-tree-sha1 = "0c667371391fc6bb31f7f12f96a56a17098b3de8"
+uuid = "872c559c-99b0-510c-b3b7-b6c96a88d5cd"
+version = "0.6.0"
+
+[[NaNMath]]
+deps = ["Compat"]
+git-tree-sha1 = "ce3b85e484a5d4c71dd5316215069311135fa9f2"
+uuid = "77ba4419-2d1f-58cd-9bb1-8ffee604a2e3"
+version = "0.3.2"
+
+[[Observables]]
+deps = ["Test"]
+git-tree-sha1 = "dc02cec22747d1d10d9f70d8a1c03432b5bfbcd0"
+uuid = "510215fc-4207-5dde-b226-833fc4488ee2"
+version = "0.2.3"
+
+[[OffsetArrays]]
+git-tree-sha1 = "1af2f79c7eaac3e019a0de41ef63335ff26a0a57"
+uuid = "6fe1bfb0-de20-5000-8ca7-80f57d26f881"
+version = "0.11.1"
+
+[[Optim]]
+deps = ["Calculus", "DiffEqDiffTools", "ForwardDiff", "LineSearches", "LinearAlgebra", "NLSolversBase", "NaNMath", "Parameters", "PositiveFactorizations", "Printf", "Random", "SparseArrays", "StatsBase", "Test"]
+git-tree-sha1 = "a626e09c1f7f019b8f3a30a8172c7b82d2f4810b"
+uuid = "429524aa-4258-5aef-a3af-852621145aeb"
+version = "0.18.1"
+
+[[OrderedCollections]]
+deps = ["Random", "Serialization", "Test"]
+git-tree-sha1 = "c4c13474d23c60d20a67b217f1d7f22a40edf8f1"
+uuid = "bac558e1-5e72-5ebc-8fee-abe8a469f55d"
+version = "1.1.0"
+
+[[OrdinaryDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "DiffEqOperators", "ExponentialUtilities", "ForwardDiff", "GenericSVD", "LinearAlgebra", "Logging", "MuladdMacro", "NLsolve", "Parameters", "RecursiveArrayTools", "Reexport", "StaticArrays"]
+git-tree-sha1 = "7481f05badc75b80a62d0da988f09d6028c4fbb1"
+uuid = "1dea7af3-3e70-54e6-95c3-0bf5283fa5ed"
+version = "5.8.1"
+
+[[PDMats]]
+deps = ["Arpack", "LinearAlgebra", "SparseArrays", "SuiteSparse", "Test"]
+git-tree-sha1 = "8b68513175b2dc4023a564cb0e917ce90e74fd69"
+uuid = "90014a1f-27ba-587c-ab20-58faa44d9150"
+version = "0.9.7"
+
+[[Parameters]]
+deps = ["Markdown", "OrderedCollections", "REPL", "Test"]
+git-tree-sha1 = "70bdbfb2bceabb15345c0b54be4544813b3444e4"
+uuid = "d96e819e-fc66-5662-9728-84c9c7592b0a"
+version = "0.10.3"
+
+[[Parsers]]
+deps = ["Dates", "Test"]
+git-tree-sha1 = "db2b35dedab3c0e46dc15996d170af07a5ab91c9"
+uuid = "69de0a69-1ddd-5017-9359-2bf0b02dc9f0"
+version = "0.3.6"
+
+[[Pidfile]]
+deps = ["FileWatching", "Test"]
+git-tree-sha1 = "1ffd82728498b5071cde851bbb7abd780d4445f3"
+uuid = "fa939f87-e72e-5be4-a000-7fc836dbe307"
+version = "1.1.0"
+
+[[Pkg]]
+deps = ["Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "UUIDs"]
+uuid = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
+
+[[PlotThemes]]
+deps = ["PlotUtils", "Requires", "Test"]
+git-tree-sha1 = "f3afd2d58e1f6ac9be2cea46e4a9083ccc1d990b"
+uuid = "ccf2f8ad-2431-5c83-bf29-c5338b663b6a"
+version = "0.3.0"
+
+[[PlotUtils]]
+deps = ["Colors", "Dates", "Printf", "Random", "Reexport", "Test"]
+git-tree-sha1 = "8e87bbb778c26f575fbe47fd7a49c7b5ca37c0c6"
+uuid = "995b91a9-d308-5afd-9ec6-746e21dbc043"
+version = "0.5.8"
+
+[[Plots]]
+deps = ["Base64", "Contour", "Dates", "FixedPointNumbers", "GR", "GeometryTypes", "JSON", "LinearAlgebra", "Measures", "NaNMath", "Pkg", "PlotThemes", "PlotUtils", "Printf", "REPL", "Random", "RecipesBase", "Reexport", "Requires", "Showoff", "SparseArrays", "Statistics", "StatsBase", "UUIDs"]
+git-tree-sha1 = "c446e51959578de01b5a4efa72ca6f2460e38196"
+uuid = "91a5bcdd-55d7-5caf-9e0b-520d859cae80"
+version = "0.25.1"
+
+[[PoissonRandom]]
+deps = ["Random", "Statistics", "Test"]
+git-tree-sha1 = "44d018211a56626288b5d3f8c6497d28c26dc850"
+uuid = "e409e4f3-bfea-5376-8464-e040bb5c01ab"
+version = "0.4.0"
+
+[[PooledArrays]]
+git-tree-sha1 = "6e8c38927cb6e9ae144f7277c753714861b27d14"
+uuid = "2dfb63ee-cc39-5dd5-95bd-886bf059d720"
+version = "0.5.2"
+
+[[PositiveFactorizations]]
+deps = ["LinearAlgebra", "Test"]
+git-tree-sha1 = "957c3dd7c33895469760ce873082fbb6b3620641"
+uuid = "85a6dd25-e78a-55b7-8502-1745935b8125"
+version = "0.2.2"
+
+[[Printf]]
+deps = ["Unicode"]
+uuid = "de0858da-6303-5e67-8744-51eddeeeb8d7"
+
+[[Profile]]
+deps = ["Printf"]
+uuid = "9abbd945-dff8-562f-b5e8-e1ebf5ef1b79"
+
+[[QuadGK]]
+deps = ["DataStructures", "LinearAlgebra"]
+git-tree-sha1 = "438630b843c210b375b2a246329200c113acc61b"
+uuid = "1fd47b50-473d-5c70-9696-f719f8f3bcdc"
+version = "2.1.0"
+
+[[REPL]]
+deps = ["InteractiveUtils", "Markdown", "Sockets"]
+uuid = "3fa0cd96-eef1-5676-8a61-b3b8758bbffb"
+
+[[Random]]
+deps = ["Serialization"]
+uuid = "9a3f8284-a2c9-5f02-9a11-845980a1fd5c"
+
+[[RandomNumbers]]
+deps = ["Random", "Requires"]
+git-tree-sha1 = "1417be19c15706c1584d01e32662eb640a4cc908"
+uuid = "e6cf234a-135c-5ec9-84dd-332b85af5143"
+version = "1.3.0"
+
+[[RecipesBase]]
+git-tree-sha1 = "7bdce29bc9b2f5660a6e5e64d64d91ec941f6aa2"
+uuid = "3cdcf5f2-1ef4-517c-9805-6587b60abb01"
+version = "0.7.0"
+
+[[RecursiveArrayTools]]
+deps = ["ArrayInterface", "RecipesBase", "Requires", "StaticArrays", "Statistics", "Test"]
+git-tree-sha1 = "187ea7dd541955102c7035a6668613bdf52022ca"
+uuid = "731186ca-8d62-57ce-b412-fbd966d074cd"
+version = "0.20.0"
+
+[[RecursiveFactorization]]
+deps = ["LinearAlgebra", "Random", "Test"]
+git-tree-sha1 = "54410ebd72cbb84d7b7678eb3da643f8e71181fc"
+uuid = "f2c3362d-daeb-58d1-803e-2bc74f2840b4"
+version = "0.0.1"
+
+[[Reexport]]
+deps = ["Pkg"]
+git-tree-sha1 = "7b1d07f411bc8ddb7977ec7f377b97b158514fe0"
+uuid = "189a3867-3050-52da-a836-e630ba90ab69"
+version = "0.2.0"
+
+[[Requires]]
+deps = ["Test"]
+git-tree-sha1 = "f6fbf4ba64d295e146e49e021207993b6b48c7d1"
+uuid = "ae029012-a4dd-5104-9daa-d747884805df"
+version = "0.5.2"
+
+[[ResettableStacks]]
+deps = ["Random", "StaticArrays", "Test"]
+git-tree-sha1 = "8b4f6cf3c97530e1ba7177ad3bc2b134373da851"
+uuid = "ae5879a3-cd67-5da8-be7f-38c6eb64a37b"
+version = "0.6.0"
+
+[[Rmath]]
+deps = ["BinaryProvider", "Libdl", "Random", "Statistics", "Test"]
+git-tree-sha1 = "9a6c758cdf73036c3239b0afbea790def1dabff9"
+uuid = "79098fc4-a85e-5d69-aa6a-4863f24498fa"
+version = "0.5.0"
+
+[[Roots]]
+deps = ["Printf", "Statistics", "Test"]
+git-tree-sha1 = "7228278e31d6d0e22a1ae0b41ea9a0df2859f33d"
+uuid = "f2b01f46-fcfa-551c-844a-d8ac1e96c665"
+version = "0.8.1"
+
+[[SHA]]
+uuid = "ea8e919c-243c-51af-8825-aaa63cd721ce"
+
+[[Serialization]]
+uuid = "9e88b42a-f829-5b0c-bbe9-9e923198166b"
+
+[[SharedArrays]]
+deps = ["Distributed", "Mmap", "Random", "Serialization"]
+uuid = "1a1011a3-84de-559e-8e89-a11a2f7dc383"
+
+[[ShiftedArrays]]
+deps = ["OffsetArrays", "RecursiveArrayTools", "Test"]
+git-tree-sha1 = "b1aa84666a23a31cebcdcb848e62428968789287"
+uuid = "1277b4bf-5013-50f5-be3d-901d8477a67a"
+version = "0.5.0"
+
+[[Showoff]]
+deps = ["Dates"]
+git-tree-sha1 = "e032c9df551fb23c9f98ae1064de074111b7bc39"
+uuid = "992d4aef-0814-514b-bc4d-f2e9a6c4116f"
+version = "0.3.1"
+
+[[Sockets]]
+uuid = "6462fe0b-24de-5631-8697-dd941f90decc"
+
+[[SortingAlgorithms]]
+deps = ["DataStructures", "Random", "Test"]
+git-tree-sha1 = "03f5898c9959f8115e30bc7226ada7d0df554ddd"
+uuid = "a2af1166-a08f-5f64-846c-94a0d3cef48c"
+version = "0.3.1"
+
+[[SparseArrays]]
+deps = ["LinearAlgebra", "Random"]
+uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
+
+[[SpecialFunctions]]
+deps = ["BinDeps", "BinaryProvider", "Libdl", "Test"]
+git-tree-sha1 = "0b45dc2e45ed77f445617b99ff2adf0f5b0f23ea"
+uuid = "276daf66-3868-5448-9aa4-cd146d93841b"
+version = "0.7.2"
+
+[[StaticArrays]]
+deps = ["LinearAlgebra", "Random", "Statistics"]
+git-tree-sha1 = "db23bbf50064c582b6f2b9b043c8e7e98ea8c0c6"
+uuid = "90137ffa-7385-5640-81b9-e52037218182"
+version = "0.11.0"
+
+[[Statistics]]
+deps = ["LinearAlgebra", "SparseArrays"]
+uuid = "10745b16-79ce-11e8-11f9-7d13ad32a3b2"
+
+[[StatsBase]]
+deps = ["DataStructures", "LinearAlgebra", "Missings", "Printf", "Random", "SortingAlgorithms", "SparseArrays", "Statistics"]
+git-tree-sha1 = "8a0f4b09c7426478ab677245ab2b0b68552143c7"
+uuid = "2913bbd2-ae8a-5f71-8c99-4fb6c76f3a91"
+version = "0.30.0"
+
+[[StatsFuns]]
+deps = ["Rmath", "SpecialFunctions", "Test"]
+git-tree-sha1 = "b3a4e86aa13c732b8a8c0ba0c3d3264f55e6bb3e"
+uuid = "4c63d2b9-4356-54db-8cca-17b64c39e42c"
+version = "0.8.0"
+
+[[StatsModels]]
+deps = ["CategoricalArrays", "DataStructures", "LinearAlgebra", "Missings", "ShiftedArrays", "SparseArrays", "StatsBase", "Tables"]
+git-tree-sha1 = "f004c23db67aeecb4bba94d08c79580af851b21b"
+uuid = "3eaba693-59b7-5ba5-a881-562e759f1c8d"
+version = "0.6.1"
+
+[[SteadyStateDiffEq]]
+deps = ["Compat", "DiffEqBase", "DiffEqCallbacks", "LinearAlgebra", "NLsolve", "Reexport", "Test"]
+git-tree-sha1 = "fe9852d18c3e30f384003da50d6049e5fbc97071"
+uuid = "9672c7b4-1e72-59bd-8a11-6ac3964bc41f"
+version = "1.4.0"
+
+[[StochasticDiffEq]]
+deps = ["DataStructures", "DiffEqBase", "DiffEqDiffTools", "DiffEqNoiseProcess", "DiffEqOperators", "FillArrays", "ForwardDiff", "LinearAlgebra", "Logging", "MuladdMacro", "NLsolve", "Parameters", "Random", "RandomNumbers", "RecursiveArrayTools", "Reexport", "StaticArrays"]
+git-tree-sha1 = "83be179dc849f11f83dcfa715c7818ef551a0f6c"
+uuid = "789caeaf-c7a9-5a7d-9973-96adeb23e2a0"
+version = "6.5.0"
+
+[[SuiteSparse]]
+deps = ["Libdl", "LinearAlgebra", "Serialization", "SparseArrays"]
+uuid = "4607b0f0-06f3-5cda-b6b1-a6196a1729e9"
+
+[[Sundials]]
+deps = ["BinaryProvider", "DataStructures", "DiffEqBase", "Libdl", "LinearAlgebra", "Logging", "Reexport", "SparseArrays", "SuiteSparse"]
+git-tree-sha1 = "9af4eb72683f0dafe84c6a5bd31aea1ebca4d46c"
+uuid = "c3572dad-4567-51f8-b174-8c6c989267f4"
+version = "3.6.1"
+
+[[TableTraits]]
+deps = ["IteratorInterfaceExtensions"]
+git-tree-sha1 = "b1ad568ba658d8cbb3b892ed5380a6f3e781a81e"
+uuid = "3783bdb8-4a98-5b6b-af9a-565f29a5fe9c"
+version = "1.0.0"
+
+[[Tables]]
+deps = ["DataValueInterfaces", "IteratorInterfaceExtensions", "LinearAlgebra", "Requires", "TableTraits", "Test"]
+git-tree-sha1 = "c93aafd5c45f850c653ec1c45857ba2151835f95"
+uuid = "bd369af6-aec1-5ad0-b16a-f7cc5008161c"
+version = "0.2.7"
+
+[[Test]]
+deps = ["Distributed", "InteractiveUtils", "Logging", "Random"]
+uuid = "8dfed614-e22c-5e08-85e1-65c5234f0b40"
+
+[[TimerOutputs]]
+deps = ["Crayons", "Printf", "Test", "Unicode"]
+git-tree-sha1 = "b80671c06f8f8bae08c55d67b5ce292c5ae2660c"
+uuid = "a759f4b9-e2f1-59dc-863e-4aeb61b1ea8f"
+version = "0.5.0"
+
+[[Tokenize]]
+git-tree-sha1 = "0de343efc07da00cd449d5b04e959ebaeeb3305d"
+uuid = "0796e94c-ce3b-5d07-9a54-7f471281c624"
+version = "0.5.4"
+
+[[Tracker]]
+deps = ["Adapt", "DiffRules", "ForwardDiff", "LinearAlgebra", "MacroTools", "NNlib", "NaNMath", "Printf", "Random", "Requires", "SpecialFunctions", "Statistics", "Test"]
+git-tree-sha1 = "327342fec6e09f68ced0c2dc5731ed475e4b696b"
+uuid = "9f7883ad-71c0-57eb-9f7f-b5c9e6d3789c"
+version = "0.2.2"
+
+[[TranscodingStreams]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "a25d8e5a28c3b1b06d3859f30757d43106791919"
+uuid = "3bb67fe8-82b1-5028-8e26-92a6c54297fa"
+version = "0.9.4"
+
+[[Trebuchet]]
+deps = ["DiffEqBase", "JSExpr", "OrdinaryDiffEq", "WebIO"]
+git-tree-sha1 = "c1daf264ca0c050381be6258b5e311615ea5f250"
+uuid = "98b73d46-197d-11e9-11eb-69a6ff759d3a"
+version = "0.1.0"
+
+[[TreeViews]]
+deps = ["Test"]
+git-tree-sha1 = "8d0d7a3fe2f30d6a7f833a5f19f7c7a5b396eae6"
+uuid = "a2a6695c-b41b-5b7d-aed9-dbfdeacea5d7"
+version = "0.3.0"
+
+[[URIParser]]
+deps = ["Test", "Unicode"]
+git-tree-sha1 = "6ddf8244220dfda2f17539fa8c9de20d6c575b69"
+uuid = "30578b45-9adc-5946-b283-645ec420af67"
+version = "0.4.0"
+
+[[UUIDs]]
+deps = ["Random", "SHA"]
+uuid = "cf7118a7-6976-5b1a-9a39-7adc72f591a4"
+
+[[Unicode]]
+uuid = "4ec0a83e-493e-50e2-b9ac-8f72acf5a8f5"
+
+[[WeakRefStrings]]
+deps = ["Random", "Test"]
+git-tree-sha1 = "9a0bb82eede528debe631b642eeb48a631a69bc2"
+uuid = "ea10d353-3f73-51f8-a26c-33c1cb351aa5"
+version = "0.6.1"
+
+[[WebIO]]
+deps = ["AssetRegistry", "Base64", "Compat", "Distributed", "FunctionalCollections", "JSON", "Logging", "Observables", "Random", "Requires", "Sockets", "UUIDs", "WebSockets", "Widgets"]
+git-tree-sha1 = "458ebbd85da851b01bed01e6321b0d8f4c7044b0"
+uuid = "0f1e0344-ec1d-5b48-a673-e5cf874b6c29"
+version = "0.8.6"
+
+[[WebSockets]]
+deps = ["Base64", "Dates", "Distributed", "HTTP", "Logging", "Random", "Sockets", "Test"]
+git-tree-sha1 = "13f763d38c7a05688938808b49cb29b18b60c8c8"
+uuid = "104b5d7c-a370-577a-8038-80a2059c5097"
+version = "1.5.2"
+
+[[Widgets]]
+deps = ["Colors", "Dates", "Observables", "OrderedCollections", "Test"]
+git-tree-sha1 = "c53befc70c6b91eaa2a9888c2f6ac2d92720a81b"
+uuid = "cc8bc4a8-27d6-5769-a93b-9d913e69aa62"
+version = "0.6.1"
+
+[[ZipFile]]
+deps = ["BinaryProvider", "Libdl", "Printf"]
+git-tree-sha1 = "580ce62b6c14244916cc28ad54f8a2e2886f843d"
+uuid = "a5390f91-8eb1-5f08-bee0-b1d1ffed6cea"
+version = "0.8.3"
+
+[[Zygote]]
+deps = ["DiffRules", "FillArrays", "ForwardDiff", "IRTools", "InteractiveUtils", "LinearAlgebra", "MacroTools", "NNlib", "NaNMath", "Random", "Requires", "SpecialFunctions", "Statistics"]
+git-tree-sha1 = "520d65c5e5554473863d738bde053f5f6769d3be"
+uuid = "e88e6eb3-aa80-5325-afca-941959d7151f"
+version = "0.3.2"
diff --git a/Courses/Differentiable Programming/Project.toml b/Courses/Differentiable Programming/Project.toml
new file mode 100644
index 0000000..3c94cc3
--- /dev/null
+++ b/Courses/Differentiable Programming/Project.toml
@@ -0,0 +1,12 @@
+[deps]
+BenchmarkTools = "6e4b80f9-dd63-53aa-95a3-0cdb28fa8baf"
+CSV = "336ed68f-0bac-5ca0-87d4-7b16caf5d00b"
+DiffEqFlux = "aae7a2af-3d4f-5e19-a356-7da93b79d9d0"
+DifferentialEquations = "0c46a032-eb83-5123-abaf-570d42b7fbaa"
+Flux = "587475ba-b771-5e3f-ad9e-33799f191a9c"
+ForwardDiff = "f6369f11-7733-5829-9624-2563aa707210"
+Literate = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
+Optim = "429524aa-4258-5aef-a3af-852621145aeb"
+Plots = "91a5bcdd-55d7-5caf-9e0b-520d859cae80"
+Trebuchet = "98b73d46-197d-11e9-11eb-69a6ff759d3a"
+Zygote = "e88e6eb3-aa80-5325-afca-941959d7151f"
diff --git a/Manifest.toml b/Manifest.toml
index fb2c933..d0f2265 100644
--- a/Manifest.toml
+++ b/Manifest.toml
@@ -4,8 +4,10 @@
uuid = "2a0f44e3-6c83-55bd-87e4-b1978d98bd5f"
[[BinaryProvider]]
-deps = ["Compat", "CredentialsHandler", "Libdl", "Pkg", "SHA", "TOML", "Test"]
+deps = ["Libdl", "Logging", "SHA"]
+git-tree-sha1 = "8153fd64131cd00a79544bb23788877741f627bb"
uuid = "b99e7846-7c00-51b0-8f62-c81ae34c0232"
+version = "0.5.5"
[[Compat]]
deps = ["Base64", "Dates", "DelimitedFiles", "Distributed", "InteractiveUtils", "LibGit2", "Libdl", "LinearAlgebra", "Markdown", "Mmap", "Pkg", "Printf", "REPL", "Random", "Serialization", "SharedArrays", "Sockets", "SparseArrays", "Statistics", "Test", "UUIDs", "Unicode"]
@@ -13,9 +15,11 @@ git-tree-sha1 = "84aa74986c5b9b898b0d1acaf3258741ee64754f"
uuid = "34da2185-b29b-5c13-b0c7-acf172513d20"
version = "2.1.0"
-[[CredentialsHandler]]
-deps = ["Base64", "HTTP", "TOML"]
-uuid = "864e158e-919d-11e8-198e-cfe890ec4681"
+[[Conda]]
+deps = ["JSON", "VersionParsing"]
+git-tree-sha1 = "9a11d428dcdc425072af4aea19ab1e8c3e01c032"
+uuid = "8f4d0f93-b110-5947-807f-2305c1781a2d"
+version = "1.3.0"
[[Dates]]
deps = ["Printf"]
@@ -26,18 +30,26 @@ deps = ["Mmap"]
uuid = "8bb1440f-4735-579b-a4ab-409b98df4dab"
[[Distributed]]
-deps = ["LinearAlgebra", "Random", "Serialization", "Sockets"]
+deps = ["Random", "Serialization", "Sockets"]
uuid = "8ba89e20-285c-5b6f-9357-94700520ee1b"
-[[HTTP]]
-deps = ["Base64", "Dates", "Distributed", "IniFile", "MbedTLS", "Sockets", "Test"]
-uuid = "cd3eb016-35fb-5094-929b-558a96fad6f3"
+[[FileWatching]]
+uuid = "7b1f6079-737a-58dc-b8bc-7a2ca5c1b5ee"
-[[IniFile]]
-uuid = "83e8ac13-25f8-5344-8a64-a9f2b223428f"
+[[Glob]]
+deps = ["Compat", "Test"]
+git-tree-sha1 = "c72f1fcb7d17426de1e8af2e948dfb3de1116eed"
+uuid = "c27321d9-0574-5035-807b-f59d2c89b15c"
+version = "1.2.0"
+
+[[IJulia]]
+deps = ["Base64", "Conda", "Dates", "InteractiveUtils", "JSON", "Markdown", "MbedTLS", "Pkg", "Printf", "REPL", "Random", "SoftGlobalScope", "Test", "UUIDs", "ZMQ"]
+git-tree-sha1 = "8eb8459d806de665f1347b25e9ad9428c2609f0f"
+uuid = "7073ff75-c697-5162-941a-fcdaad2a7d2a"
+version = "1.18.1"
[[InteractiveUtils]]
-deps = ["LinearAlgebra", "Markdown"]
+deps = ["Markdown"]
uuid = "b77e0a4c-d291-57a0-90e8-8db25a27a240"
[[JSON]]
@@ -46,14 +58,6 @@ git-tree-sha1 = "1f7a25b53ec67f5e9422f1f551ee216503f4a0fa"
uuid = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
version = "0.20.0"
-[[JuliaAcademyData]]
-deps = ["Pkg"]
-git-tree-sha1 = "6cc6db29d6560619be88d0075d697047eb484f92"
-repo-rev = "master"
-repo-url = "https://github.com/JuliaComputing/JuliaAcademyData.jl"
-uuid = "18b7da76-0988-5e3b-acac-6290be3a708f"
-version = "0.1.0"
-
[[LibGit2]]
uuid = "76f85450-5226-5b5a-8eaa-529ad045b433"
@@ -78,14 +82,16 @@ deps = ["Base64"]
uuid = "d6f4376e-aef5-505a-96c1-9c027394607a"
[[MbedTLS]]
-deps = ["BinaryProvider", "Dates", "Libdl", "Pkg", "Random", "Sockets"]
+deps = ["BinaryProvider", "Dates", "Distributed", "Libdl", "Random", "Sockets", "Test"]
+git-tree-sha1 = "2d94286a9c2f52c63a16146bb86fd6cdfbf677c6"
uuid = "739be429-bea8-5141-9913-cc70e7f3736d"
+version = "0.6.8"
[[Mmap]]
uuid = "a63ad114-7e13-5084-954f-fe012c677804"
[[Pkg]]
-deps = ["BinaryProvider", "CredentialsHandler", "Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "TOML", "UUIDs"]
+deps = ["Dates", "LibGit2", "Markdown", "Printf", "REPL", "Random", "SHA", "UUIDs"]
uuid = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"
[[Printf]]
@@ -113,6 +119,12 @@ uuid = "1a1011a3-84de-559e-8e89-a11a2f7dc383"
[[Sockets]]
uuid = "6462fe0b-24de-5631-8697-dd941f90decc"
+[[SoftGlobalScope]]
+deps = ["Test"]
+git-tree-sha1 = "012661b70364840fcd380912d878d96f7bf95ff3"
+uuid = "b85f4697-e234-5449-a836-ec8e2f98b302"
+version = "1.0.10"
+
[[SparseArrays]]
deps = ["LinearAlgebra", "Random"]
uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
@@ -121,17 +133,25 @@ uuid = "2f01184e-e22b-5df5-ae63-d93ebab69eaf"
deps = ["LinearAlgebra", "SparseArrays"]
uuid = "10745b16-79ce-11e8-11f9-7d13ad32a3b2"
-[[TOML]]
-deps = ["Dates"]
-uuid = "9d418dce-91a8-11e8-0173-7b01a971d501"
-
[[Test]]
deps = ["Distributed", "InteractiveUtils", "Logging", "Random"]
uuid = "8dfed614-e22c-5e08-85e1-65c5234f0b40"
[[UUIDs]]
-deps = ["Random"]
+deps = ["Random", "SHA"]
uuid = "cf7118a7-6976-5b1a-9a39-7adc72f591a4"
[[Unicode]]
uuid = "4ec0a83e-493e-50e2-b9ac-8f72acf5a8f5"
+
+[[VersionParsing]]
+deps = ["Compat"]
+git-tree-sha1 = "c9d5aa108588b978bd859554660c8a5c4f2f7669"
+uuid = "81def892-9a0e-5fdd-b105-ffc91e053289"
+version = "1.1.3"
+
+[[ZMQ]]
+deps = ["BinaryProvider", "FileWatching", "Libdl", "Sockets", "Test"]
+git-tree-sha1 = "34e7ac2d1d59d19d0e86bde99f1f02262bfa1613"
+uuid = "c2297ded-f4af-51ae-bb23-16f91089e4e1"
+version = "1.0.0"
diff --git a/Project.toml b/Project.toml
index ebae8eb..116ec28 100644
--- a/Project.toml
+++ b/Project.toml
@@ -3,7 +3,9 @@ uuid = "a2de2ff4-d7bb-11e8-2879-f9ef9fa2c94f"
version = "0.1.0"
[deps]
-JuliaAcademyData = "18b7da76-0988-5e3b-acac-6290be3a708f"
+Glob = "c27321d9-0574-5035-807b-f59d2c89b15c"
+IJulia = "7073ff75-c697-5162-941a-fcdaad2a7d2a"
+JSON = "682c06a0-de6a-54ab-a142-c8b1cf79cde6"
Literate = "98b081ad-f1c9-55d3-8b20-4c87d4299306"
Pkg = "44cfe95a-1eb2-52ea-b672-e2afdf69b78f"